基于D数理论的不确定多属性决策方法

王宁奎,魏代俊

(湖北民族学院 理学院,湖北 恩施 445000)



基于D数理论的不确定多属性决策方法

王宁奎,魏代俊*

(湖北民族学院 理学院,湖北 恩施 445000)

摘要：针对不确定多属性决策过程中信息缺失且关联时难以决策的问题,提出了一种基于D数理论的计算方法.该方法通过属性权重值的大小来决定D数融合顺序,如果权重值相等,则按照D数客观评估值大小顺序融合.该方法结合D数理论可实现属性信息缺失与关联时的不确定信息下的多属性决策,最后通过汽车引擎选择实例验证了该方法的有效性与可行性.

关键词：评估决策；不确定信息；D数理论；D数融合

证据理论最初由Dempster于1967年提出,并于1976年由其学生Shafer加以完善[1-2].Dempster 提出了集值映射的概念,并定义了上下概率[1],在1976年,Shafer用基本概率指派函数重新诠释了上下概率,建立完善的证据数学理论[2].

同时D数理论还在不断发展完善.针对D数融合规则不满足交换律的问题,其博士生邓鑫洋为D数融合提出了一种融合顺序,按D数权重值大小融合D数.如果权重值相同,则所有可能的融合结果均被计算出来,其中D数集成最大值为最优融合结果,D数集成最小值为最差融合结果.但同时它带来的问题是,当D数权重值相等的时候,计算出所有可能的融合结果的计算量相当大.针对这个不足,本文提出了一种新的计算方法,如果D数的权重值不相等,则首先按照D数权重值的大小顺序融合.而当D数权重值相等的时候,则按照D数自身的评价值大小融合.

1基本知识简介

1.1D-S理论(D-S theory)[1-2]

D-S理论定义Θ为识别框架,它是由相互独立的元素组成的集合.Θ的幂集是由辨识框架中所有元素的子集构成的集合,表示成2Θ.定义概率指派函数m:2Θ→[0,1],使得：

(1)

其中:∅为空集,A为辨识框架的幂集中的元素.m称为基本概率指派函数(BPA)且0≤m(A)≤1,m(A)表示对命题A的信任程度.如果m(A)>0,A称为一个焦元,所有焦元的集合称为核.

Dempster组合规则是证据理论的核心部分,它可以用于融合多组证据.设m1,m2,…,mn为辨识框架下的n个基本信任指派函数.其融合规则m=m1⊕m2⊕m3⊕…⊕mn定义为:

(2)

1.2D数理论[12]

作为证据理论的推广,D数理论扩展了证据理论中元素互斥与完备的假设.设Ω为非空集合,D数是一个映射D:D→[0,1],使得:

(3)

其中∅为空集,B是集合Ω的一个子集.可以发现,D数理论与证据理论的定义很相似,然而他们在本质上存在着很大差异,用下面一个例子来说明两个理论之间的区别.

假设两种方法被用于评估一辆汽车.评价分数表示在区间[0,100]上,在证据理论中,一名专家可以给出他的评估结果为：m({a1})=0.3,m({a2})=0.5,m({a1,a2,a3})=0.2；

其中:a1=[1,30],a2=[31,68],a3=[67,100],显然a1,a2与a3相互独立且信任函数之和为1. 集合(a1,a2,a3)为辨识框架.另一个人用D数表示评估结果为：D({b1})=0.3,D({b2})=0.5,D({b1,b2,b3})=0.1.

其中:b1=[1,30],b2=[24,68],b3=[60,100],显然a1,a2与a3并非相互独立,且对每个b的信任程度之和小于1.从实际情况看,这两种评价都有存在的可能.

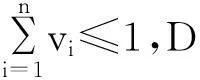
或者被简单得写成：

D={(b1,v1)(b2,v2)(b3,v3)…(bn,vn)}.

定义2(D数融合规则)：令D1,D2为两个D数：

D1,D2的融合表示为D=D1⊕D2,其定义为:D({b})=v.

由D数的融合规则可以发现,多个D数相互融合的时候并不满足交换律.为此,邓鑫洋于2014年给出了一种D数融合顺序[14].

定义4令D1,D2,…,Dn为n个D数,uj为每个D数的顺序变量,表示为(uj,Duj),多个D数融合定义为fD,使得：

其中:Dλi为(uj,Duj)中的Duj,它有第i小的值uj.

在文献[14]中,每一个D数是一个专家对于客观事物的主观评价,而每个专家相对是存在着相对重要性的,所以在多元D数融合的过程中,专家的权重定义为这个D数的顺序变量.当顺序变量为一样的值时,一种最优最差的融合规则被定义了.所有可能的融合结果均被计算出来,而D数集成最大与最小的值被定义为最优与最差的融合结果.但是这种融合方法计算量相当大,对于n个D数,需要进行n!次融合.

2基于D数理论的不确定多属性决策方法

2.1一种新的D数融合规则

本文提出了一种新的基于D数理论的多属性决策计算方法.给定每个D数一个顺序变量,首先按照顺序变量融合.当顺序变量相同时,则按D数的客观评价等级值大小作为融合顺序.

由D数融合规则可以发现,先融合的评估值对最后的评价结果影响较小,而后融合的评估等级则为最后的融合结果作出更大的贡献.所以,对于一般形式表示的D数,当顺序变量相同的时候,可以选取两种融合顺序,一是按照客观评价值(即b值)从大到小融合,而当客观等级评价值完全一样时,此时按照D数集成的值从大到小融合.另一种恰好相反,先按照客观评价值b从小到大,若当客观评价等级相同时,就按照D数集成从小到大融合.例如,对于下面三个D数：D1={(1,1)};D2={(3,1)};D3={(5,1)}.

其中:三个D数的顺序变量值(本例为权重)相等ω1=ω2=ω3,那么接下来就考虑b值,本例中有5>3>1,所以按照b值从大到小的融合顺序为D=D3⊕D2⊕D1.按照b值从小到大的融合顺序为D=D1⊕D2⊕D3.

2.2D数应用于汽车引擎评估

汽车引擎之于汽车相当于大脑之于人类,它是汽车的核心部分.汽车引擎的评估是一件复杂的事情,因为在评估的过程中有大量的人工主观判断,数据含有不确定性.同时,因为专家的认知水平的局限性,评估数据中含有充分的不完备性.所以现有的方法在处理汽车引擎的评估问题的时候存在着一定的问题.文献[3]中利用证据推理方法评估汽车引擎,证据推理方法的计算过程相对比较复杂,本文则利用提出的D数理论新方法评估汽车引擎的优劣.

汽车引擎的优劣受很多因素的影响,其中最主要的影响因素为：反应能力,油耗量,声音大小,震感以及加速度.分别记为：R=反应能力,F=油耗量,Q=声音大小,V=震感以及S=加速度.在文献[3]中,每个影响因素同等重要,也即其权重ωR=ωF=ωQ=ωV=ωS.对于文献[3]中的4个引擎,专家对以上5个方面分别作出评价,评估等级风别为：{差(P),不重要的(I),一般(A),好(G),很好(E)}

对于引擎1,专家给出其相应的评估数据.对于反应能力,专家100%确认它的评估等级为好,所以评估可以表示为D数{(G,1)}.对于声音大小的评估,专家50%确认评估水平为好,30%的肯定性确认评估等级为很好,还有20%却因为人工评估时的不确定性,对该引擎的认识不足等原因不确定该评估为什么等级.所以对于声音大小这一评估标准,专家给出的评估等级可以用D数表示为：D(Q)={(G,0.5)(E,0.3)}(其中0.5+0.3<1).同样的道理,专家对于引擎1,分别从5个方面给出了如下的评价：

利用同样的方法,专家分别对其它4个引擎进行评估,评估结果如表1所示.

表1　专家为4个引擎的评估

在表1中,每一个引擎在某一些方面评估结果都比较优秀,可以大致看出引擎2在反应能力方面比其他的引擎更优,引擎4在油耗量与声音大小方面比其他引擎更优.然而,综合评价结果哪个引擎更优秀却无法简单判别.此时,D数的融合规则将用于融合所有的5个方面,得到最终的综合评价结果.而所有的评估等级均为语意的评价,所以在融合之前首先将所有语意评估等级数字化,在此采用文献[3]效应函数为标准,设：

则表1中的所有语言评价均转化为D数的数值表示,如表2所示.

表2　专家为4个引擎的评估数值评价

本文的D数融合方法用于综合每个引擎的5个评价标准.本文中,指标的权重当作是每个D数的顺序变量.而本文中每个评价指标的权重值相等,也就是ωR=ωF=ωQ=ωV=ωS,所以本文按照客观评价值b的值作为融合顺序,而当客观评价值相同时,则考虑D数集成的值的大小.对引擎1,按照客观评价值从小到大的融合顺序为D=D(F)⊕D(Q)⊕D(V)⊕D(R)⊕D(S).反之,按客观评价值从大到小的融合顺序为D=D(S)⊕D(R)⊕D(V)⊕D(Q)⊕D(F).通过这两种计算方法将D数融合以后,D数集成值即为该引擎的综合评估等级.所有引擎的评估结果如表3所示.

从表3可以看出,按b值从小到大的排序为：0.840 625>0.684 4>0.572 9>0.409 1.

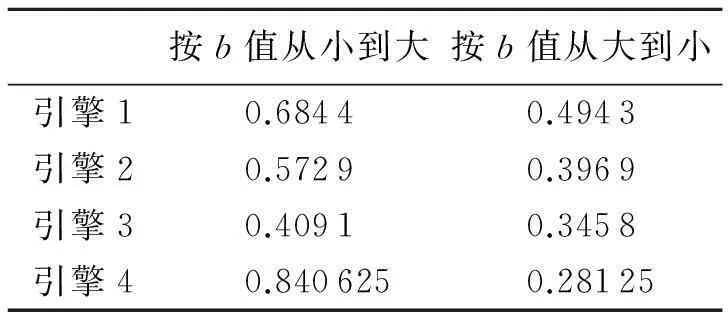
表3　引擎评估的融合结果

对应的汽车引擎排序为：“引擎4>引擎1>引擎2>引擎3” 其中‘>’表示更优于.按b值从大到小的排序为:0.494 3>0.396 9>0.345 8>0.281 25,对应的汽车引擎排序为：“引擎1>引擎2>引擎3>引擎4”.

在文献[3]中,综合评估结果排序为：“引擎1>引擎2>引擎4>引擎3”,本文的评价结果按照b值从大到小与文献[3]比较,均找到了最好的引擎为引擎1,引擎2次之,引擎3与4则相对较差.而如果按照b值从小到大的排序则相差较大.从这个角度比较,在本例汽车引擎选择中按照b值从大到小的融合较为合理.本例结果表明,本文提出的新的D数融合算法融合次数减少,降低了计算复杂度,同时也能得到合理的评价结果.

3结语

证据理论作为概率理论的延伸已经在许多方面得到广泛应用.然而,证据理论是建立在辨识框架中的元素相互独立且基本概率指派函数完备的假设基础上的,这在现实生活应用中存在一定的局限性.生活中用于评价的定性指标之间就并非相互独立,也可能会因为认知水平的局限性导致信息收集的不完备性.D数理论,又进一步推广了证据理论,扩展了证据理论中各元素互斥,基本概率指派函数完备的假设,使得其在现实生活中得到更加广泛地应用.本文较详尽地介绍了D-S证据理论与D数理论,并且针对现有的D数融合顺序计算量较大的问题,提出了一种合理简单的融合方法.并将该方法应用于汽车引擎评估中.算例验证了本文中的方法的简单性,合理性,说明了D数在处理不确定信息的有效性、可行性.

参考文献:

[1]DEMPSTER A P.Upper and lower probabilities induced by a multivalued mapping [J].Annals of Mathematical Statistics,1967,38(2): 325-339.

[2]SHAFER G.A mathematical theory of evidence[M].Princeton: Princeton University Press,1976.

[3]YANG J B,XU D L.Nonlinear Information Aggregation via Evidential reasoning in Multiattribute Decision Analysis Under Uncertainty [J].IEEE Transactions on systems,man and cybernetics-Part A: systems and humans,2002,32(3):376-393.

[4]WEI D J,DENG X Y,ZHANG X G,et al. Identifying influentialnodes in weighted networks based on evidence theory [J].Physica AStatistical Mechanics & Its Applications,2013,392(10):2564-2575.

[5]CHEN S Y,DENG Y,WU J Y.Fuzzy sensor fusion based on evidence theory and its application[J].Applied Artificial Intelligence,2013,27(3):235-248.

[6]吴润秀.一种结合DS证据理论的改进KNN分类算法[J].统计与决策,2015(15):16-19.

[7]徐晓东.基D-证据理论和聚集系数的重要节点挖掘算法[J].信息系统工程,2015(4):126-126.

[8]SU X Y,MAHADEVAN S,XU P D,et al.Dependence Assessment in Human Reliability Analysis Using Evidence Theory and AHP[J].Risk Analysis,2015,35(7):1296-1316.

[9]DEZERT J.Foundations for a new theory of plausible and paradoxical reasoning[J].Information and Security,2002,9(1):13-57.

[10]SMARANDACHE F,DEZERT J.An introduction to the DSm theory for the combination of paradoxical,uncertain,and imprecise sources of information[J].Octogon Mathematical Magazine,2007,15(2):681-722.

[11]SMETS P,KENNES R.The transferable belief model [J].Artificial Intelligence,1994,66(2):191-234.

[12]DENG Y.D numbers: Theory and Applications [J].Journal of Information & Computational Science,2012,9(9):2421-2428.

[13]DENG X Y,HU Y,DENG Y.Bridge Condition Assessment Using D Numbers[J].The Scientific World Journal,2014,2014:571-578.

[14]DENG X Y,HU Y,DENG Y.Mahadevan S.Environmental impact assessment basedon D numbers [J].Expert Systems with Applications,2014,41(2):635-643.

[15]DENG X Y,HU Y,DENG Y,Mahadevan S.Supplier selection using AHP methodology extended by D numbers [J].Expert Systems with Applications,2014,41(1):156-167.

[16]FAN G C,ZHONG D H,YAN F G,et al.A hybrid fuzzy evaluation methodfor curtain grouting efficiency assessment based on an AHP methodextended by D numbers [J].Expert Systems with Applications,2016,44(1):289-303.

[17]DENG X Y,LU X,CHAN F T,et al.D-CFPR:D numbers extended consistent fuzzy preference relations [J].Knowledge-Based Systems,2015,73:61-68.

[18]LIU H C,YOU J X,FAN X J,et al.Failure mode and effects analysis using D numbers and grey relationalprojection method [J].Expert Systems with Applications,2014,41(14):4670-4679.

责任编辑：时凌

Uncertain Multiattribute Decision Making Method Based on D Numbers

WANG Ningkui,WEI Daijun*

(School of Science,Hubei University for Nationalities,Enshi 445000,China)

Abstract：For the problem of multiple attribute decision making because of the information of uncertainty and incompleteness,a basic computing method based on D numbers theory is proposed in this paper.The weights of the attributes are regarded as the order when multiple D numbers get combined.When the weights are of equal value,the objective assessment grades represented by D numbers are considered.The proposed method has overcome the deficiencies in uncertain multiple attributes decision making caused by the uncertainty because of information shortage and high conflict. The numerical example of evaluating the motor engine shows the efficiency and feasibility of the proposed method.

Key words：assessment and decision making;uncertainty;D numbers;D numbers fusion

收稿日期：2016-02-18.

基金项目：湖北省教育厅科学研究计划重点项目(D20151902);湖北民族学院博士启动项目(MY2014B003);湖北省大学生创新创业训练项目(20140517018).

作者简介：王宁奎(1990- ),男,硕士生,主要从事信息融合的研究；*通信作者：魏代俊(1977- ),男,博士,副教授,主要从事信息融合与复杂网络研究.

文章编号：1008-8423(2016)01-0035-05

DOI:10.13501/j.cnki.42-1569/n.2016.03.009

中图分类号：O232

文献标志码：A