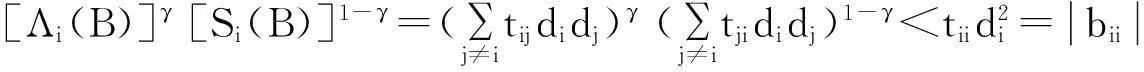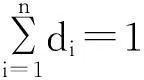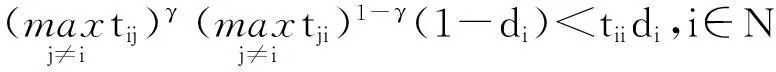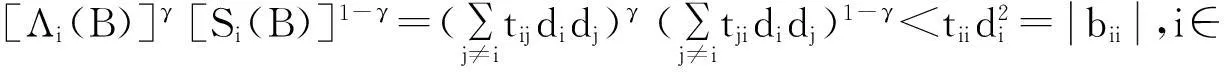块γ-链对角占优矩阵的判定

李艳艳

(文山学院 数学学院，云南 文山 663000)



块γ-链对角占优矩阵的判定

李艳艳

(文山学院 数学学院，云南 文山 663000)

摘要：利用块γ-链对角占优矩阵的性质和不等式的一些放缩方法，得到了块γ-链对角占优矩阵的判定定理，该定理只与矩阵的元素有关，易于计算.

关键词：块H-矩阵；块对角占优矩阵；块严格γ-链对角占优矩阵

1预备知识

设Cn×n(Rn×n)分别表示复(实)矩阵的集合，N={1，2，…,n}，K={1,2,…,k}.

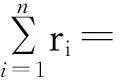
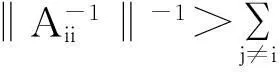
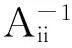
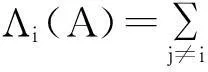
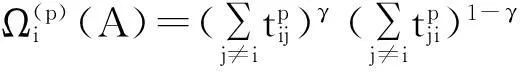
定义2[2]对于分块矩阵A，若存在γ∈[0,1]，使得∀i∈N，都有:tii≥[Λi(A)]γ[Si(A)]1-γ成立，就称A为块γ-链对角占优矩阵；若上式中的等号是严格的，则称A为块严格γ-链对角占优矩阵.

引理1[2]对于分块矩阵A，若A为块严格γ-链对角占优矩阵，则A是块H-矩阵.

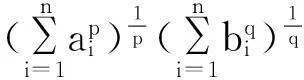
引理3[2]若a≥b≥0,c≥d≥0,γ∈[0,1]，则(a-b)γ(c-d)1-γ≤aγc1-γ-bγd1-γ.

2块γ-链对角占优矩阵的判定

关于块H-矩阵的判定是一热点问题，许多学者在这方面都做出了卓有成效的贡献[3-8].本部分利用块γ-链对角占优矩阵的性质和不等式的一些放缩方法，得到了块γ-链对角占优矩阵的判定定理.

定理1设A=(aij)∈Cn×n，若存在γ∈[0,1]，使A满足下列条件之一，A就为块H-矩阵.

证明先证明第一个条件.如果条件(1)成立，令:

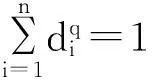
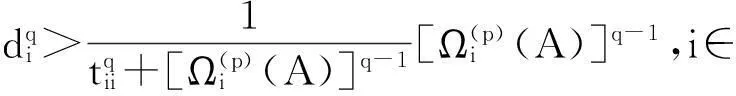
应用引理1，∀i∈N有下面的不等式成立.

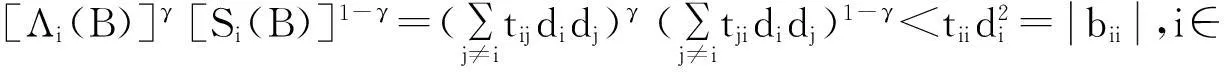
则DAD是块严格γ-链对角占优矩阵，故A是块H-矩阵.

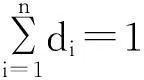
即:[Λi(A)]γ[Si(A)]1-γ(1-di)

则DAD是块严格γ-链对角占优矩阵，故A是块H-矩阵.

参考文献:

[1]黄庭祝，杨传胜.特殊矩阵分析及应用[M].北京：科学出版社，2006：1-4.

[2]薛媛,刘建州.γ-链对角占优矩阵与H-矩阵的判定[J].工程数学学报,2015,32(5):709-718.

[3]李艳艳,黄卫华.广义α1对角占优矩阵的判定准则[J].湖北民族学院学报(自然科学版)，2015，33(2)：156-158.

[4]李朝迁.M-矩阵最小特征估计及其相关问题研究[D].昆明：云南大学,2014.

[5]Wei-wei Zhou,Zhong Xu,Quan Lu,et at.Criteria for Generalized Strictlyα-Diagonally Dominant Matrices and Nonsingular H-matrices[C]//Proceeding of the sixth International Conference of Matrices and Operators,Chengdu,China,July 8-11,2011：286-289.

[6]PANG M X，MAO G P.Generalizations of Diagonal Dominance for Matrices and Its Applications[J].J of Math.Research Exposition,1991,11(4):507-509.

[7]高中喜，黄廷祝，刘福体.块H-矩阵的简洁判据[J].工程数学学报,2004(3):340-344.

[8]JUN Ruyin,ZHONG Xu,QUAN Lu.New Sufficient Conditions for NonsingularH-matrices[C]//Proceeding of the sixth International Conference of Matrices and Operators,Chengdu,China,July 8-11,2011:369-372.

责任编辑：时凌

Determination of Blockγ- diagonally Dominant Matrix

LI Yanyan

(School of Mathematics,Wenshan University,Wenshan 663000，China)

Abstract：By using some properties of block γ- diagonally dominant matrix and some scaling method of inequality,got the theorem of block γ- diagonally dominant matrix,which is only related to the elements of matrix and easy to calculate.

Key words：block H-matrix;block diagonally dominant matrix;block strictly γ- diagonally dominant matrix

收稿日期：2016-01-18.

基金项目：云南省教育厅科学研究项目(2013Y585).

作者简介：李艳艳(1982- )，女，硕士，讲师，主要从事矩阵理论及其应用的研究.

文章编号：1008-8423(2016)01-0029-02

DOI:10.13501/j.cnki.42-1569/n.2016.03.007

中图分类号：O151.21

文献标志码：A