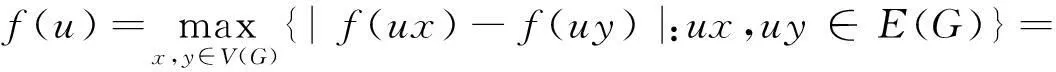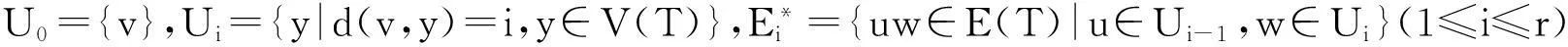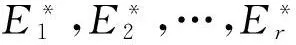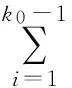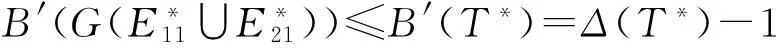树的边带宽与叶子数

杜先云,任秋道,文华燕

(1.成都信息工程学院 数学学院，四川 成都 610225;2.绵阳师范学院 数学与计算机科学学院,四川 绵阳 621000；3.西南科技大学 城市学院，四川 绵阳 621000)



树的边带宽与叶子数

杜先云1,任秋道2,文华燕3

(1.成都信息工程学院 数学学院，四川 成都 610225;2.绵阳师范学院 数学与计算机科学学院,四川 绵阳 621000；3.西南科技大学 城市学院，四川 绵阳 621000)

摘要：图G边的一个标号f是指边集E(G)到集合{1,2,…,m}之间的一个一一映射，即:∀e∈E(G),∃t,1≤t≤m，使得f(e)=t.图G的边带宽B′(G)=minBf′(G)，其中Bf′(G)=max{|f(uv)-f(uw)|：uv,uw∈E(G)}.给出树T的边带宽满足「(m-1)/(d-1)⎤≤B′(T)≤l-s，0≤s≤l/2，其中d为树T的直径，l为树T的叶子数.而且k(为偶数)元正则树的边带宽B′(T*)≤l/2，广义星图T*的边带宽B′(T*)=l或l-1.

关键词：独立邻边集；边带宽；树；叶子数

本文图G是无向有限连通图，顶点集与边集分别是V(G)和E(G).图G边的一个标号f是指边集E(G)到自然数的子集{1,2,…,m}(m表示G的边数)之间的一个一一映射，即:∀e∈E(G),∃t∈N+,1≤t≤m，使得f(e)=t.图G的边带宽B′(G)=minBf′(G)，其中Bf′(G)=max{|f(uv)-f(uw)|:uv,uw∈E(G)}.对于一个标号f，若B′(G)=Bf′(G)，称这个标号为图G的边带宽标号[1-6].可以类似定义图G的点带宽，它来源于研究数值矩阵的逆，寻找图的带宽是一个NP问题.D.Eichhorn等人已完成了θ图的边带宽[2].给出两类3—正则图的边带宽[3].本文用树的叶子数来刻画树T的边带宽的界.

我们容易知道：图G带宽B′(G)≥Δ-1，其中Δ是图G的最大度.下面给出一个引理.

引理1存在uv∈E(G)，使得图G的边带宽B′(G)≥d(u)+d(v)-2，其中d(u)，d(v)分别表示顶点u和v的度[6].

证明令Γ(uv)={uiv:uiv∈E(G),1≤i≤d(v)}∪{uvj:uvj∈E(G),1≤j≤d(u)}，则有|Γ(uv)|=d(u)+d(v)-1.若f(uv)≤min{f(e):e∈Γ(uv)}，存在e′∈Γ(uv)使得f(e′)≥f(uv)+|Γ(uv)|-1.因此，Bf′(G)≥f(e′)-f(uv)≥d(u)+d(v)-2.对于f(uv)≥max{f(e):e∈Γ(uv)}，有类似结论.对于xy∈E(G)，设在Γ(xy)中标号最小或最大标号边记为uv，对于边uv应用该结论可得：Bf′(G)≥d(u)+d(v)-2.由于标号f的任意性，则有：存在uv∈E(G)，使得B′(G)≥d(u)+d(v)-2.

推论1设图G是k-正则图，则有B′(G)≥2(k-1).

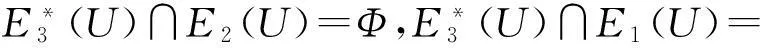
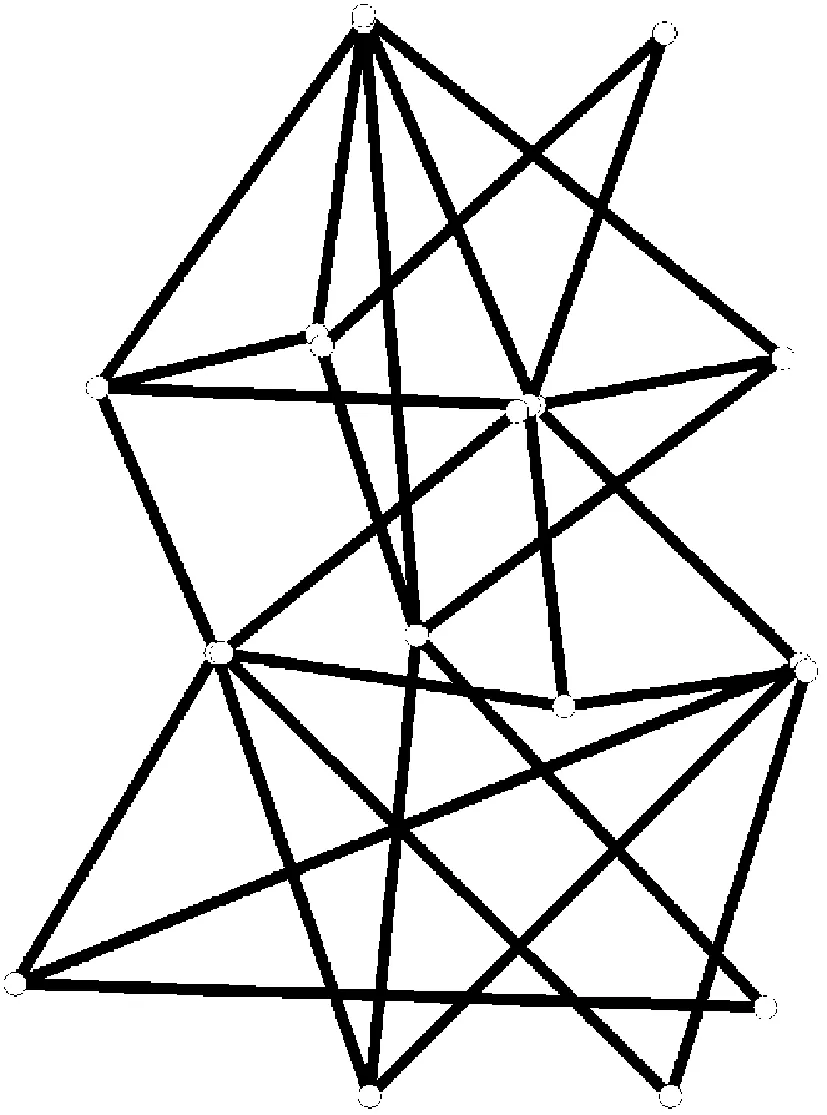
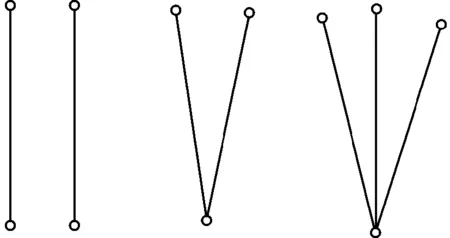
图1　图的独立邻边集分解Fig.1　A decompositiom of independent edge set of a graph

引理2保证了图G边集的正交分解.可以这样来形象理解：拿着图G一些顶点一抖，就把G的顶点分成n+1层，从而把G的边集分为n层.如图1.

定理1连通图G的边带宽B′(G)≥「(m-1)/(d-1)⎤，d为图G的直径.

证明标号f是图G的边集到集合{1,2,…,m}之间的一一映射.从标号最小的边到标号最大的边之间有一条路pn=u0u1…un，该路上点的邻边编号差的绝对值等于或小于B′(G).为了方便，令:

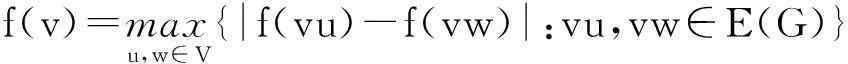
假设f(u1)=f(u2)=…=f(un-1)=B′(G)达到最大来估计图G的边带宽.该路上的边标号分别是:f(u0u1)=1,f(uiui+1)=1+iB′(G)(1≤i≤n-1).

现在来说明路pn是点u0和un之间的短程线.若点ui(0≤i≤n-2)和uj(j≥i+2)有边uiuj，它的标号介于边ui-1ui和uiui+1的标号之间，令:

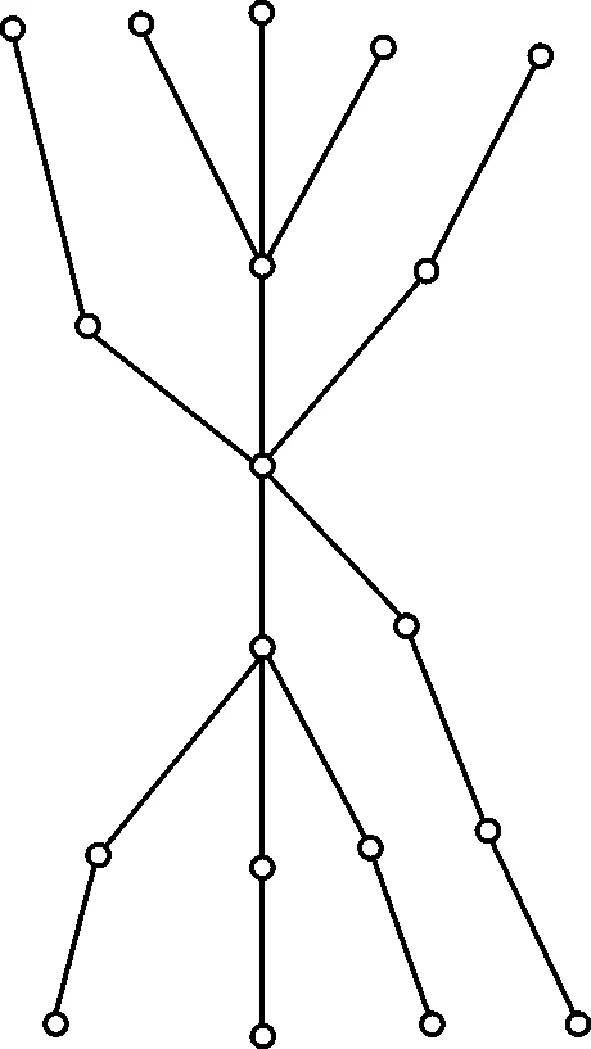
f(uiuj)=1+(i-1)B′(G)+k (1≤k

则有:f(uj)=f(ujuj+1)-f(uiuj)=(j-i+1)B′(G)-k>B′(G).

矛盾.因此点u0和un之间的距离是n.根据f(un-1un)=1+(n-1)B′(G)≥m，可得B′(G)≥「(m-1)/(n-1)⎤.由于图G的最长路的边数是直径d，因此，B′(G)≥「(m-1)/(d-1)⎤.证毕.

图2　图)的边的关联情况Fig.2　A decompositiom of The categories of the related edges of the tragh )

定义2设T是一棵树，悬挂点的集合为V′={v|d(v)=1}.如果存在点x，使得x和任意悬挂点v之间的距离都相等，即d(x,u)=d(x,v),u,v∈V′，称树T为理想树，点x为树根[5].

引理3理想树T的边带宽不超过叶子数.

给点u2的未编号的边排序如下：

给点us的关联边中还未编号的边排序如下：

对于1≤k≤s-1，

定理3树的边带宽不超过叶子数.

把k条路xiyi…zi(1≤i≤k)的全部始点xi粘合在一起构成的图，称为广义星图，记为T*.我们知道：星图的边带宽比叶子数少1.

推论2广义星图T*的边带宽比叶子数少1或等于叶子数.

(ii)如果图T*是由k条长度大于1的不同路构成，其中最长路的长度为r.把长度小于r的所有路增加边变成长度为r的路，类似(i)可得，B(T*)=k.

图3　构造树T′=T1′+T2′Fig.3　The comtructeal

定理4树T的边带宽满足B′(T)≤l-s，0≤s≤l/2，其中l为树T的叶子数.

由定理2可得:树T的边带宽满足:B′(T)≤B′(T′)≤max{Δ(T),s,l-s}.

发现有很多树的边带宽不超过叶子数的一半.如：路和k(为偶数)元正则树的边带宽.

推论3k元正则树T的边带宽满足：当k为偶数时，B′(T)≤kr/2；当k为奇数时，B′(T)≤(kr+kr-1)/2，其中r(≥2)为树T的半径.

证明半径为r的k元正则树T的叶子数为kr，树根为v.现在把T分解成两颗半径为r，树根均为v的理想树T1和T2.当k为偶数时，T1和T2的叶子数均为kr/2，当k为奇数时，T1的叶子数为(kr-kr-1)/2，T2的叶子数为(kr+kr-1)/2.根据定理4可得结论.证毕.

对于复杂的图，由于与度为2的点相邻的边对图的边带宽没有贡献，可将这样的边收缩掉.例如：将长度大于2的路收缩为长度为2的路，将长度大于3的圈收缩为长度为3的圈.经过边收缩后的图可以更好地研究图的边带宽.

参考文献:

[1]EICHHORN D,MUBAYI D,WEST D B.The edge-bandwidth of theta graphs[J].Graph Theory,2000(35): 89-98.

[2]PESK G W,SHASTRI A.Bandwidth of theta graphs with short paths[J].Discrete Mathematics,1992(103):177-187.

[3]Papadimitriou.The NP-completeness of the bandwidth minimization problem[J].Computing,1976(16):263-270.

[4]GAREY M R,GRAHAM R L,JOHNSON D S,et al.Complexity results for bandwidth minimization[J].SIAM J Applmath,1978,34:477-495.

[5]SMITHLINE L.Bandwidth of the compkletek-ary tree[J].Discrete Mathematics,1995,142:203-212.

[6]任秋道,黄琼湘.完全图的边带宽的另一证明[J].绵阳师范学院学报,2005(2):12-17.

[7]陈玲,任秋道,岳华.两类3-正则图的边带宽[J].新疆师范学大学院学报,2008(1):23-26.

[8]杜先云,任秋道.图Cmk(P2,…，P2,Pl)的最大特征值[J].四川师范大学学报(自然科学版),2009,32(1):64-67.

[9]任秋道,何继标,黄琼湘.圈的定向距离图的性质[J].四川师范大学学报(自然科学版),2007,30(2):185-187.

[10]任秋道,汪元伦.圈的定向距离图的阶[J].四川师范大学学报(自然科学版),2005,28(2):63-65.

责任编辑：时凌

The Edge-bandwidth of a Tree and its Number of Leaves

DU Xianyun1,REN Qiudao2,WEN Huayan3

(1.College of Mathematics of Chengdu University of Information Technology,Chengdu 610225,China;2.Department of Mathematics and Information Science of Mianyang Normal University,Mianyang 621000,China;3.City College,Southwest University of Science and Technology,Mianyang 621000,China)

Abstract：A label f of an edge in a graph G refers to one-mapping from the edge set E(G)to the set {1,2,…,m},namely:∀e∈E(G),∃t,1≤t≤m,satisying f(e)=t.The edge-bandwidth of a graph B′(G)=minBf′(G),wherein Bf′(G)=max{|f(uv)-f(uw)|:uv,uw∈E(G)}.The paper obtains that the inequalities 「(m-1)/(d-1)⎤≤B′(T)≤l-s，0≤s≤l/2，wherein d is the diameter of a tree and l is the number of its leaves.Moreover the edge-bandwidth of a k(even)-regular tree T satisfies the inequalities B′(T)≤l/2,and the edge-bandwidth of a generalized star graph T* does B′(T*)=l or l-1.

Key words：independent adjacent edge- set;edge bandwidth；tree;number of leaves

收稿日期：2016-03-21.

基金项目：四川省教育厅自然科学基金项目(15114931).

作者简介：杜先云(1964-)，男，教授，主要从事应用数学的研究.

文章编号：1008-8423(2016)01-0001-04

DOI:10.13501/j.cnki.42-1569/n.2016.03.001

中图分类号：O175

文献标志码：A