小波变换-回归分析模型在轨道不平顺检测中的应用

胡燚斌，王　冠，邢　俊，张　攀，王　平

（西南交通大学高速铁路线路工程教育部重点实验室，四川成都　610031）



小波变换-回归分析模型在轨道不平顺检测中的应用

胡燚斌，王冠，邢俊，张攀，王平

（西南交通大学高速铁路线路工程教育部重点实验室，四川成都610031）

摘要基于车辆-轨道耦合动力学理论，以CRH2动车组为例建立车辆-轨道一体化模型。根据实测高铁轨向不平顺数据计算出车体横向加速度，并结合小波变换法和回归分析法分析了轨向不平顺与车体响应的关系，找出引起车体横向振动的不利波段并确定其产生位置，为高铁养护维修提供理论支撑。研究结果表明：小波变换-回归分析模型既能确定敏感波段又能给出其里程，是一种有效的时频分析方法；轨向不平顺与车体横向加速度存在较明显的线性关系；CRH2动车组速度250 km/h时，轨向不平顺8～16 m，16～32 m波长为引起车体横向振动的最不利波段，通过小波变换法可以给出其对应的里程。

关键词小波变换-回归分析模型；轨道不平顺；车辆轨道耦合动力学；时频分析

高速铁路对轨道几何形位尤其是轨道不平顺的管理和控制要求极高。评价轨道不平顺通常利用轨道质量指数（Track Quality Index，TQI）和轨道谱［1-4］。轨道质量指数反映不平顺幅值，不能反映轨道不平顺波长的分布。仅通过幅值来控制轨道的平顺性会造成不必要的过大的调整量［5-6］。轨道谱分析是评价轨道整体平顺性的有效方法，可给出轨道不平顺幅值和波长，但缺乏定位功能，难以应用。

小波变换作为一种时频分析方法，不但能给出不平顺幅值和波长，而且具有较为精确的定位功能［7］。回归分析是研究因变量和自变量关系的最广泛研究方法之一，能够较为准确地反映出2组数据的关系。本文通过将小波变换和回归分析法结合起来，分析轨道几何不平顺与车体响应的关系，找出引起车体横向振动的不利波段及其产生位置，给线路养护维修提供依据。

1　小波变换-回归分析模型

1. 1小波变换原理

小波变换是对信号的时间、频率进行局部化分析，具有高频部分时间细分、低频部分频率细分的特点。小波母函数ψ（x）为平方可积函数，经过时间平移和尺度伸缩，可以得到小波簇，形式为

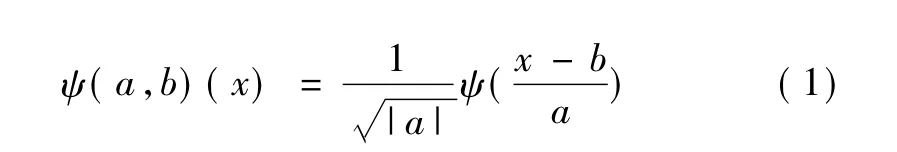
式中：a为伸缩因子；b为平移因子。

对信号f（x）的连续小波变换Wf（a，b）定义为

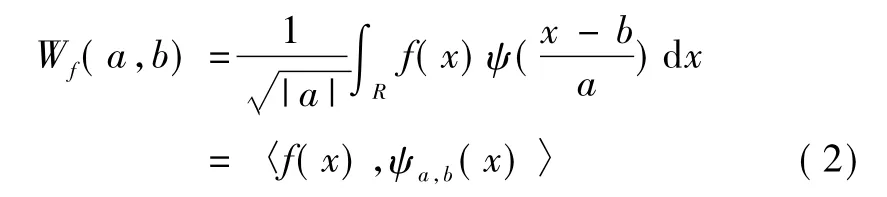
其逆变换（重构信号）为

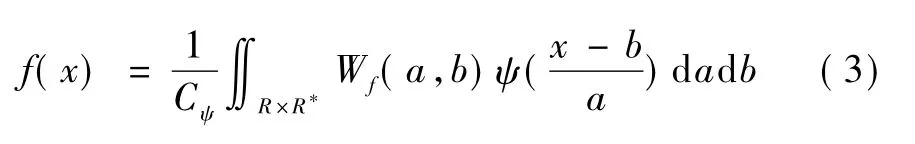
对于信号f（x），x = 1，2，…，n，需要对a，b进行离散化处理，目前普遍采用的是二维离散的处理形式。离散小波变换定义为

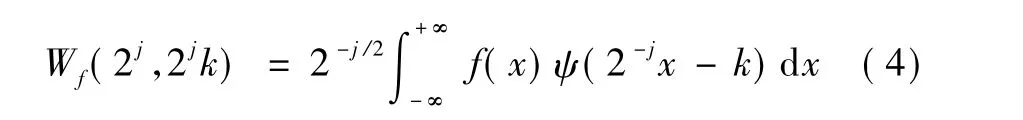
式中：2j，2jk为离散后的伸缩因子和平移因子。其逆变换（重构信号）为

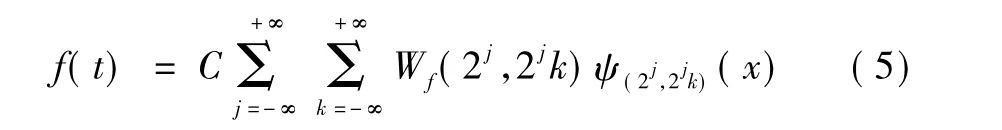
式中，C是一个与信号无关的常数。

Mallat提出了离散小波变换，即金字塔算法。任何函数XL2（R）都可以分解为高频部分的D1和低频部分的A1，再对低频部分A1继续分解，如图1所示。分解关系式为

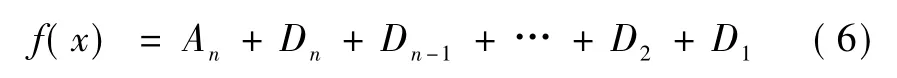
式中：Ai（i = 1，2，…，n）代表低频近似部分；Di代表高频细节部分；n代表分解层数［8］。

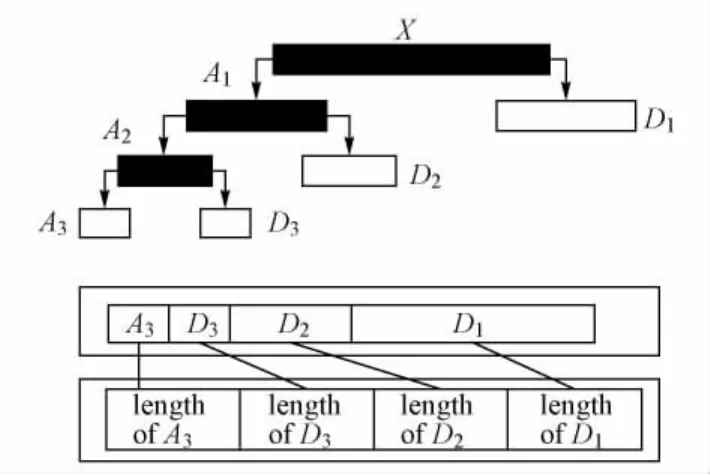
图1　小波分解原理

1. 2回归分析

回归分析是确定2种或2种以上变量间相互依赖的定量关系的一种统计分析方法［9］。本文分析轨向不平顺与车体横向加速度的关系，采用一元线性回归分析，并使用Pearson相关系数来检验二者之间的线性相关程度，表达式为

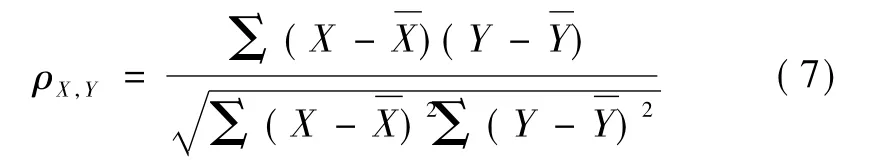
1. 3小波变换-回归分析模型

将小波变换和回归分析结合起来，建立小波变换-回归分析模型，结合车辆-轨道耦合动力学仿真，研究不同波段轨向不平顺与车体横向加速度的关系。分析步骤：①根据动检车实测数据，得到左轨向不平顺；②运用小波变换原理，将左轨向不平顺分层，分析每层所含有的能量；③应用动力学软件建立车辆-轨道耦合动力学模型，得到每层对应的车体横向加速度响应；④将各层不平顺与其对应的车体横向加速度作标准差后进行回归分析，给出不同波段的轨向不平顺与车体横向加速度的关系。

2　应用实例

2. 1轨向不平顺与车体横向加速度的关系

选取某高铁动检车实测的6 km左轨向不平顺作为样本，见图2，采样间隔为0. 25 m。为了消除平纵断面曲线、路桥过渡段的影响，所选段落为直线段。

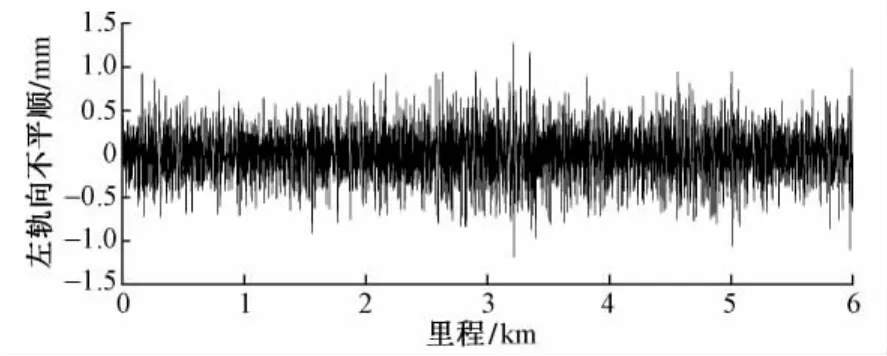
图2　左轨向不平顺样本

应用动力学软件建立车辆-轨道耦合动力学模型进行仿真分析。车辆采用CRH2动车组模型，速度为250 km/h。计算得到的车体横向振动加速度见图3。

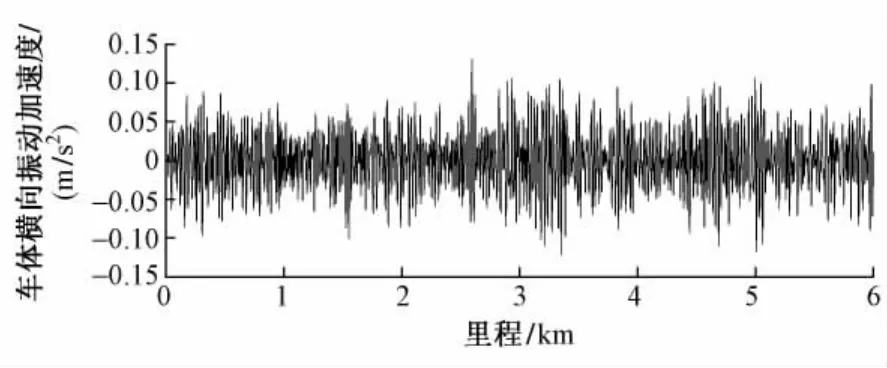
图3　车体横向振动加速度

将左轨向不平顺和车体横向加速度每200 m求标准差（移动步长为50 m）后，进行回归分析，结果见图4。回归方程为Y = 0. 163 3X + 0. 007 2。

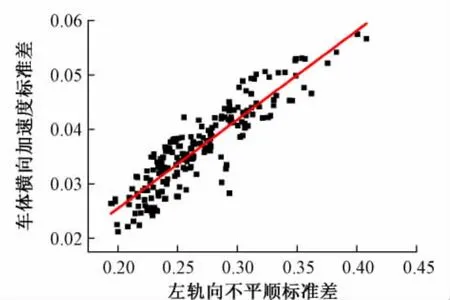
图4　回归分析结果

由图4可知，左轨向不平顺与车体横向加速度之间存在较为明显的线性关系。其相关系数ρX，Y= 0. 898 9＞0. 8，说明二者之间具有很强的线性相关性。

下面运用小波变换-回归分析模型进一步分析左轨向不平顺与车体横向加速度的关系。

2. 2小波变换

左轨向不平顺小波分层见表1。

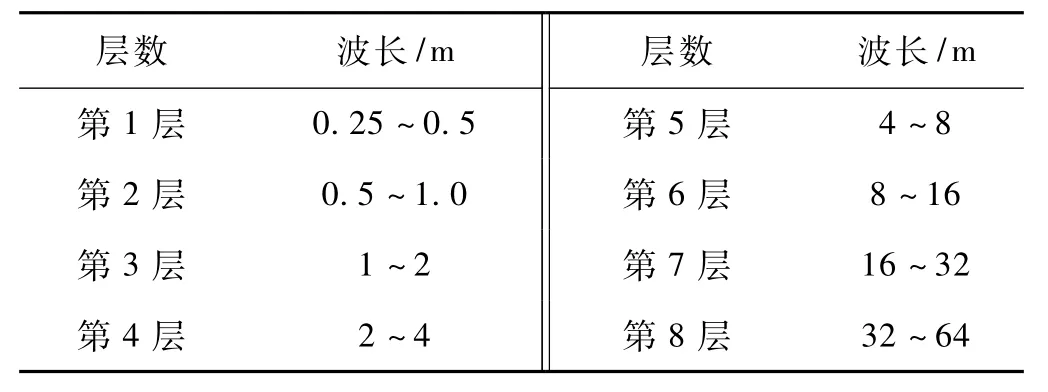
表1　左轨向不平顺小波分层

由于此段线路动检车检测波长是1. 5～42. 0 m，所以对第1，2层不予分析。分解后的各波段左轨向不平顺见图5。

舍去第1，2层（波长0. 25～0. 5 m，0. 5～1. 0 m的波段），将分解后的各波长成分重构，并与原始的轨向不平顺加以对比，见图6。可见，即使舍去了某些波长成分，重构后轨向不平顺与原始轨向不平顺基本一致。

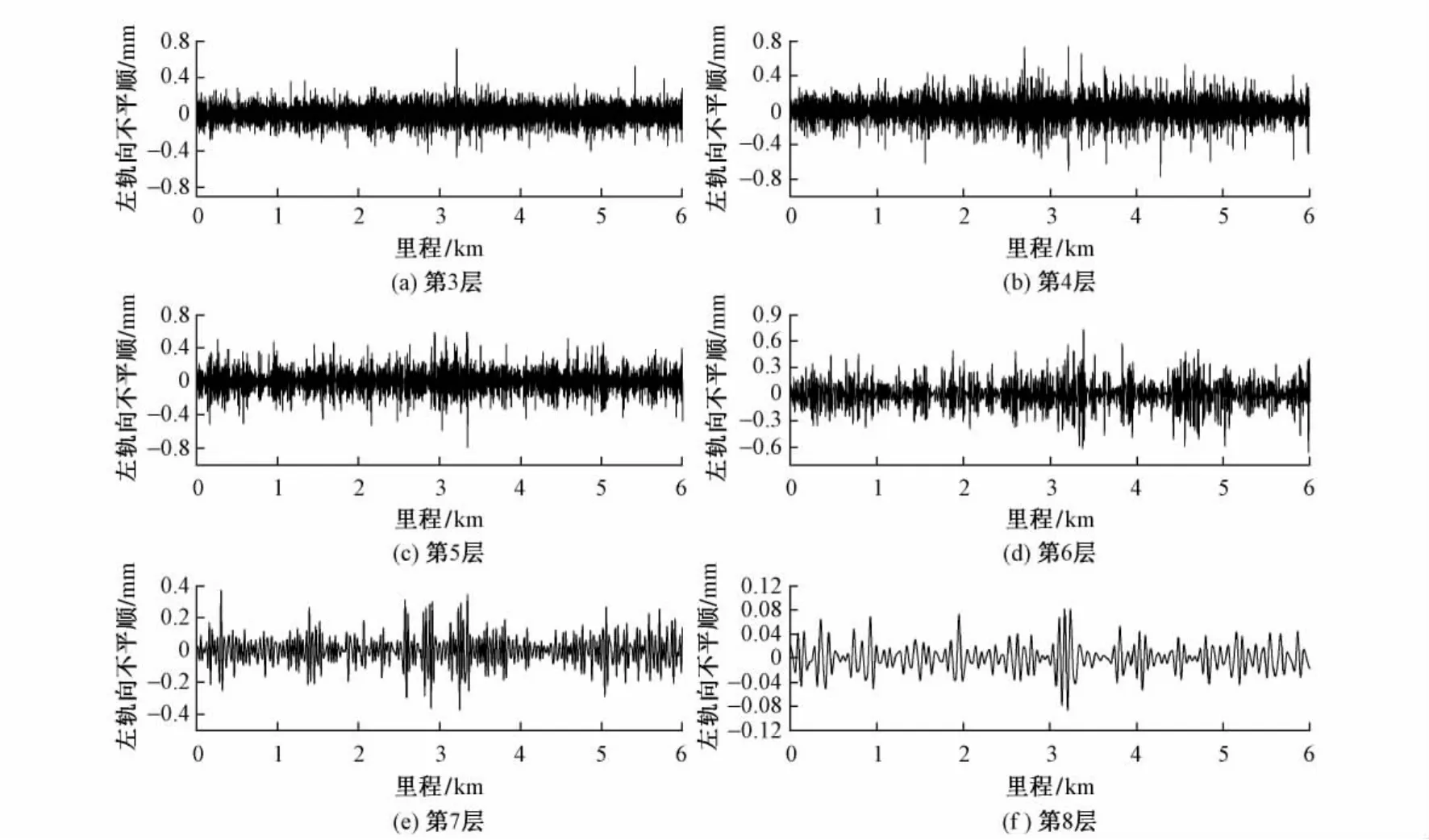
图5　各波段左轨向不平顺

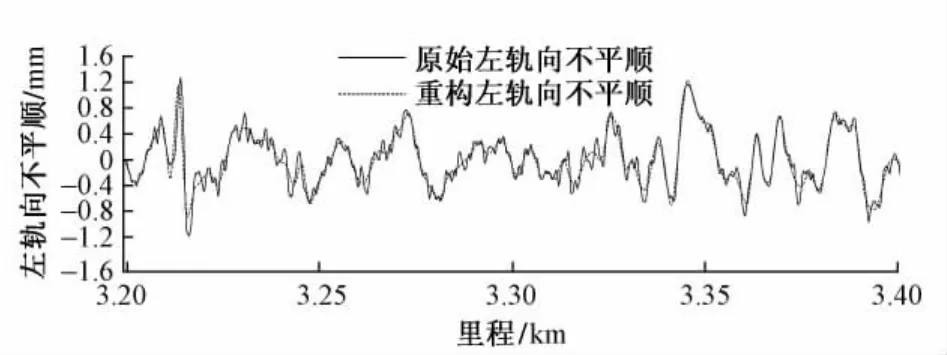
图6　重构后左轨向不平顺与原始左轨向不平顺对比

2. 3回归分析

将每层左轨向不平顺进行车辆-轨道耦合动力学仿真分析，得到对应的车体横向加速度，将二者每200 m求标准差（移动步长为50 m）后，进行回归分析，结果见图7。

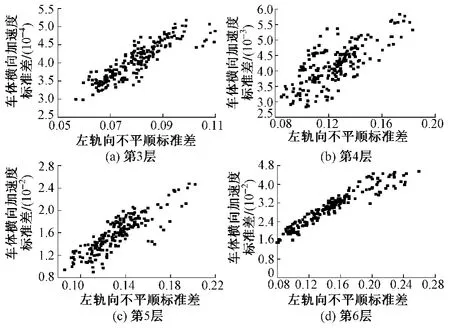
图7　各波段轨向不平顺与车体横向加速度回归分析结果

由图7可知，每层轨向不平顺标准差与车体横向加速度标准差呈良好的线性关系，故采用一元线性回归分析，方程为Y = Ax + B。分层回归分析结果见表2。

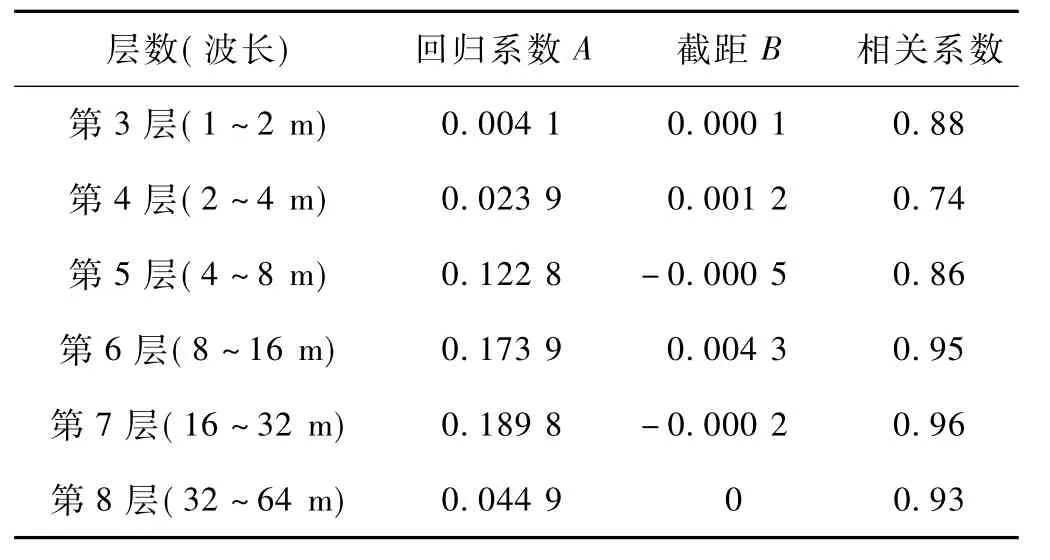
表2　分层回归分析结果

由表2可知：B值很小，可以忽略；除第4层外，其余各层的左轨向不平顺标准差与车体横向加速度标准差的Pearson相关系数都在0. 75以上，属于强相关和极强相关，证明此回归方程的拟合度较高；左轨向不平顺第5，6，7层回归系数A较大，第6，7层回归系数最大，对应波长分别为8～16 m和16～32 m，说明这2个波段为引起车体横向振动的最不利波段。

对第6，7层左轨向不平顺作进一步分析，结合图5（d）、图5（e）可以发现：第6层（波长8～16 m）在里程473，2 600，3 360，5 960 m等处左轨向不平顺出现较大幅值；第7层（波长16～32 m）在里程305，1 393，2 577，2 914，3 345，5 057 m等处左轨向不平顺出现较大幅值。调整这几处的轨向不平顺可以有效降低车体横向加速度。

3　结论

小波变换-回归分析模型为轨道不平顺检测提供了一种新的时频分析方法。应用该模型，结合车辆-轨道耦合动力学仿真，对沪昆高铁某段动检车实测轨道不平顺数据进行了分析。结果表明：

1）轨向不平顺与车体横向加速度存在较为明显的线性关系。

2）行车速度250 km/h、运营车辆为CRH2型车时，轨向不平顺8～16 m，16～32 m波段为引起车体横向振动的最不利波段。

3）给出了最不利波段中不平顺幅值较大的几处的里程。

4）小波变换-回归分析模型作为一种时频分析方法运用于轨道不平顺的分析中，不但能确定敏感波段，还能够给出里程信息，可以很好地指导现场养护维修工作。

参考文献

［1］罗林.轨道随机干扰函数［J］.中国铁道科学，1982，3（1）：74-112.

［2］罗林，张格明，吴旺青，等.轮轨系统轨道不平顺状态的控制［M］.北京：中国铁道出版社，2006.

［3］蔡文锋.遂渝线无砟轨道不平顺统计规律研究［D］.成都：西南交通大学，2008.

［4］陈宪麦.轨道不平顺时频域分析及预测方法的研究［D］.北京：铁道部科学研究院，2006.

［5］刘金朝，刘秀波.轨道质量状态评价方法［J］.铁路技术创新，2012（1）：106-109.

［6］刘秀波.轨道不平顺谱研究［D］.北京：北京交通大学，2006.

［7］陈宪麦，王澜，陶夏新，等.基于小波分析理论的轨道不平顺分析［J］.铁道工程学报，2008（1）：57-61，71.

［8］杨建国.小波变换及其工程应用［M］.北京：机械工业出版社，2005.

［9］何晓群，刘文卿.应用回归分析［M］. 3版.北京：中国人民大学出版社，2011.

（责任审编李付军）

Application of Wavelet Transform-Regression Analysis Model in Track Irregularity Inspection

HU Yibin，WANG Guan，XING Jun，ZHANG Pan，WANG Ping
（MOE Key Laboratory of High-speed Railway Engineering，Southwest Jiaotong University，Chengdu Sichuan 610031，China）

AbstractBased on the vehicle-track coupling dynamics theory，a vehicle-track integrated model was built in the case of CRH2EM U . T he lateral acceleration of vehicle body according to the measured track alignment irregularity data of high speed railway was calculated，the relations between track alignment irregularity and vehicle body response was analyzed by combining with wavelet transform and regression analysis method，and the unfavorable wave bands producing the lateral vibration of vehicle body and the accurate positions of them were determined，which could provide a theoretical support for the maintenance and repair of high speed railway. T he results showed that wavelet transform-regression analysis model is an effective time frequency analysis method which could not only detect the sensitive wave bands but also determine the accurate positions，there is a obvious linear relationship between the track alignment irregularity and the lateral acceleration of the vehicle body. On condition that CRH2 speed 250 km /h，the most unfavorable wave bands producing vehicle body lateral vibration are track alignment irregularity wave length 8～16 m and 16～32 m. T he accurate positions could be determined by using wavelet transform method.

Key wordsW avelet transform-regression analysis model；T rack irregularity；Vehicle-track coupling dynamics；T ime frequency analysis

中图分类号U216. 3

文献标识码A

DOI：10. 3969 /j. issn. 1003-1995. 2016. 05. 33

文章编号：1003-1995（2016）05-0148-04

收稿日期：2015-10-22；修回日期：2015-12-19

基金项目：中国铁道总公司科技研究开发计划（2013G001-A-1；2015G002-A）

作者简介：胡燚斌（1992—），男，硕士研究生。