一种基于有限状态机的主控程序状态转移模型

鲁梦昆， 何　涛， 余　飞

(1 湖北工业大学现代制造质量工程重点实验室，湖北 武汉 430068；2 湖北工业大学机械工程学院，湖北 武汉 430068)

一种基于有限状态机的主控程序状态转移模型

鲁梦昆1,2， 何涛1,2， 余飞1,2

(1 湖北工业大学现代制造质量工程重点实验室，湖北 武汉 430068；2 湖北工业大学机械工程学院，湖北 武汉 430068)

[摘要]自动化程度高的机器设备在运行过程中接收到外部信号或指令时可作出实时反应，但其复杂的控制程序因缺乏理论模型而难以设计。通过对有限状态机原理进行数学分析，应用有限状态机原理，设计出用状态转移图表示的主控程序状态转移模型。其特点是在机器设备的不同运行阶段，与该阶段对应的主控程序状态拥有控制主导权。此模型成功应用于“全自动编织袋套袋机研发项目”PLC主控程序设计，且此模型设计机器自动化主控程序，可以大幅提高机器设备的自动化程度与运作稳定性，状态的转移与条件的关系更清晰。

[关键词]有限状态机； 主控程序； 状态转移； PLC； 编织袋套袋机

系统主控程序简称主程序，是用来设置系统的操作环境、启动事件循环的最高一级程序。有限状态机(Finite State Machine)又称有限状态自动机，是用来表示有限个状态以及这些状态之间转移和动作等行为的数学模型。在计算机控制领域，“状态机”是一种系统设计的规范方法，应用于基于C语言、EDA、LabVIEW及FPGA/CPLD等平台的各种控制程序中[1]，使编程更容易，程序结构更简单,程序的调试、修改与扩展更方便。状态机原理适用于分支流程多、状态间的跳转较复杂的程序，通过对状态转移条件及状态寄存器进行编码，各编码实际作为指针参与程序运行，从而简化程序运行流程。此特点决定了由大量外部检测及输入信号驱动的高自动化机器设备也非常适合采用有限状态机原理进行设计。

1有限状态机的基本原理

1.1有限状态机基本构成

有限状态机是为研究有限状态的计算过程而抽象出的一种数学模型。按照输出与输入的关系可将状态机分为两类：若输出只与状态有关而与输入无关，则称为Moore状态机；输出不仅与状态有关而且与输入有关，则称为Mealy状态机，也称为经典状态机。经典状态机原理如图1所示。

图 1　经典状态机原理图

图中，x(t)为当前输入；z(t)为当前输出；状态寄存器输出s(t)为现态；组合逻辑电路输出s(t+1)为次态，clear为状态清除信号，clk为外部时钟信号。

现态s(t)在当前输入x(t)条件下进行逻辑组合得到次态s(t+1)，存储于状态寄存器中，也是当前输出，即z(t)=s(t+1)=s(t)×x(t)。当再次接受到当前输入信号x(t+1)时，下一运行周期开始，s(t+1)成为现态。

有限状态机基本构成包括以下几部分：一个有限状态集，用于表示系统中的全部状态；一个输入集，用于表示系统接受的全部输入信息；一个状态转移规则集，用于表示系统在接收到不同输入时从某一状态转移到另一状态的规则[2]。经典状态机的基本原理包含以下数学参数及关系：

有限输入集合

有限状态集合

其中P0为初始状态。

状态转移函数

P(n+1)=Pn×xn

1.2将控制程序基础结构转换为有限状态机数学模型

复杂的控制程序结构都是由大量的基础结构组合而成。基础结构包括顺序结构、分支结构和循环结构[3]，将控制程序基础结构中的各程序段视为状态机的不同状态P，控制程序一般是依据操作者的命令、传感器的输入信号或内部程序执行的不同结果进行转移[4]，这些信号可视为状态机的输入I，程序的执行过程实际是程序在不同状态之间的转移，因此控制程序具有有限状态机的特征，可利用有限状态机数学模型进行分析(图2)。

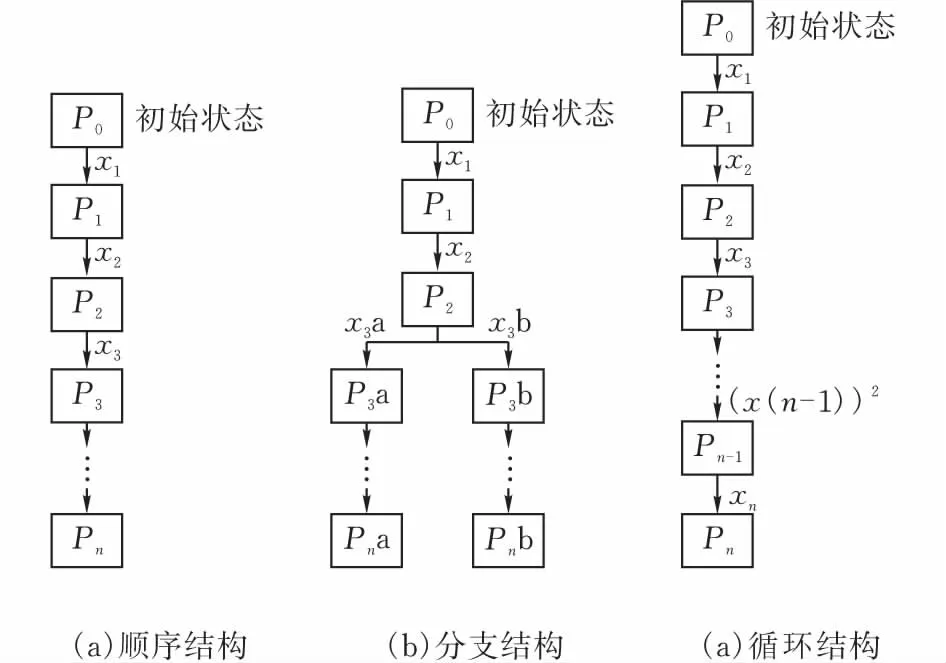
图 2　控制程序基础结构转换的有限状态机数据学模型

图2a是控制程序的顺序结构，

Pn=P0×x1×x2×x3×…×xn

由此得知，顺序结构中最终状态取决于初始状态及各状态间的转移条件。

图2b是控制程序的分支结构，

Pna=P0×x1×x2×x3×…×xna，

Pnb=P0×x1×x2×x3×…×xnb

由此得知，分支结构中最终状态取决于初始状态及各分支状态之间的转移条件。

图2c是控制程序的循环结构，

Pn=P0×x1×x2×…×xn-1×xn⟹Pn-1=

P0×x1×x2×…×xn-1

于是

由计算结果得知，循环结构中，退出循环的状态只与进入循环时的状态和返回循环的状态转移条件有关，故无论循环多少次，只要不改变循环返还条件，最终状态就不改变。

综上所述，最终状态Pn是初始状态P0在状态转移条件下进行逻辑运算的结果，均可用含有初始状态P0及转移条件的方程式表示。

1.3利用有限状态机数学模型对状态转移图分级处理的研究

对于复杂的状态机，可以将其进行分级处理。对图3a中的状态转移图进行逻辑运算分析。

图 3　状态转换图的分级处理

对于A区域，设有限输入集

有限状态集为

其中P3a是初始状态；状态转移函数

Pm×xm=P(m+1)

则此区域构成一个简单的状态机，定义为PA。

PA=P(m-1)a=P3a×x4a×x5a,…,x(m-1)a

对于B区域，设有限输入集

有限状态集

其中P3b是初始状态；状态转移函数

P(n+1)=Pn×xn，

则此区域构成一个简单的状态机，定义为

将A区域与B区域直接用PA，PB代替，得到此状态机的最简二分支结构见图3b。

运用上述理论，可对比较复杂的状态机进行分级，将其简化，子状态机视为复杂状态机的一个状态。在子状态机中，各状态间的转移独立运算，不影响上级状态机的运行，同级别的状态机运算优先级相同，将这种状态机称为多级状态机。实际应用时，可赋予子状态机唯一二进制编码，存放于独立内存单元中，需要时进行调用。

将状态机的数学模型应用于机器设备的自动化控制系统，机器设备的不同状态P对应状态集，P0为初始状态；操作者的命令与传感器的输入信号x对应输入集，状态间的转移路线对应状态转移规则，机械控制程序即可应用有限状态机进行设计。

2基于状态机原理建立主控程序状态转移模型

2.1基于有限状态机分级原理确定主控程序中的各状态

根据上述有限状态机原理的分级原理，将主控程序细分为几个大规模且级别相同的子状态，每个子状态机含有独立运行程序，列出各状态间的转移条件。一般主控系统中主要有开机、停止、复位和暂停等4个状态，其中停止和复位并非立即完成，需要一定的时间，所以将停止状态细分为“停止过程中”及“停止完成”两个状态，将复位状态细分为“复位过程中”及“复位完成”两个状态，从“停止过程中”状态转移到“停止完成状态”，与“复位过程中”状态转移到“复位完成”状态，其状态转移条件在一定时间后必定完成。

开机状态-当机器刚刚上电后的起始状态；

停止过程中状态-机器从接到停止命令开始执行停止程序到停止彻底完成前的状态；

停止完成状态-机器停止彻底完成时的状态；

复位过程中状态-机器从接到复位命令开始执行复位动作到复位动作全部完成前的状态；

复位完成状态-机器复位动作全部完成，可开始运行时的状态；

暂停状态-机器在运行过程中，临时停止并且可以根据需求继续运行时的状态。

对于大型机械自动化控制系统，为确保人工操作安全，需要设计一些特殊功能，这些功能属于状态的附属属性，必须建立在某稳定状态上。例如：机器运行过程中需要暂停后进行人工操作取出样品检测，那么可在暂停状态附加手动允许功能。需注意的是，并非随时都允许手动。

2.2由主控程序中的各状态确定状态间的关系

状态转移模型的状态转移规则：1)从一种状态转移到另一种状态一定是有触发条件的，该触发条件有限并且可知；2)由于主控程序中各状态的状态级别相同，从某一状态进入另一状态后会退出原状态，所以控制程序一定处于且仅处于一种状态，从而实现控制主导权的转移；3)某一稳定状态在特定的条件下，可以衍生出附属属性，附属属性与原状态同时消亡，定义为衍生环；4)某一状态在一段时间后必定转移到另一状态，原状态无法长时间存活，定义为封闭环。

2.3由主控程序状态间的关系建立主控程序状态转移模型

由以上得出的主控程序的各状态及状态间的关系可以建立基于状态机的主控程序状态转移模型(图4)。

图 4　基于状态机的主控程序状态转移模型

图4中，方框表示状态P，圆形表示状态的附属功能(function)，有向线表示状态转移方向，有向线上附加的条件是状态转移条件。

图中基于状态机的主控程序状态转移模型，可获得以下控制策略：

1)开机以后必须先进入停止状态，清除停机之前的状态数据，再进入其他状态，防止残留状态及输入给PLC控制程序带来不稳定因素；

2)因停止时需要一定时间清除程序中残余数据，停止动作中与停止完成状态构成封闭环；

3)系统处于停止完成状态，当接收到复位命令，系统退出停止完成状态，进入复位动作中状态，此时手动允许功能作为停止完成状态的衍生属性，与停止完成状态一同退出，之后不允许人工手动操作；

4)因复位动作需要一定时间完成，复位动作中状态与复位完成状态构成封闭环；

5)系统处于复位完成状态，当接到运行命令，系统将退出复位完成状态，进入运行状态并稳定于该状态；

6)系统处于运行状态，当接到暂停命令时，系统将退出运行状态，进入并稳定于暂停状态；

7)系统处于暂停状态，当接到继续运行命令后退出暂停状态，进入运行状态，特定动作手动允许功能作为暂停状态的衍生属性将与暂停状态一并退出，之后禁止手动操作；

8)系统处于运行状态，当检测到运行目标已达成时，进入运行目标完成状态，在此状态系统会自动触发停止命令，退出运行状态，进入停止状态。

3结束语

本文对有限状态机原理进行数学分析，研究利用状态机原理建立主控程序状态转移模型，然后将此模型应用于“全自动编织袋套袋机研发项目”的PLC主控程序设计。该机器设备实际运行结果表明，在主控程序中应用主控程序状态转移模型有以下优点：

1)程序结构清晰，有助于程序的调试、维护；

2)程序自动化程度高，稳定性好，当机器运行过程中出现卡袋等异常状况时，暂停命令可自行触发，方便运行过程中处理异常状况或抽样检测，当设定的生产目标达到时，机器可自动停止。

该模型很可能适用于不同编程环境的多数大型自动化系统，在进一步的研究中，将尝试对其进行更广泛应用。

[参考文献]

[1]叶枫桦,周新聪,白秀琴,等.基于LabVIEW队列状态机的数据采集系统设计[J]. 现代电子技术，2010，33(4):204-207,210.

[2]Linz P. An introduction to formal languages and automata[M].北京：机械工业出版社，2005.

[3]职燕,蒋存波,徐健,等.一种基于消息传递的单片机多条件多分支程序设计方法[J]. 桂林工学院学报，2005，25(1)：123-127.

[4]陈小琴,蒋存波,金红.状态机原理在控制程序设计中的应用[J].制造业自动化， 2007，29(10):57-60.

[责任编校： 张众]

A Master Control Program State Transfer Model Based on Finite State Machine

LU Mengkun1, HE Tao1, YU Fei2

(1HubeiKeyLabofModernManufactureQualityEngin,Wuhan430068,China;2SchoolofMechanicalEngin,HubeiUniv.ofTech.,Wuhan430068,China)

Abstract：After receiving the outside signals, highly automated machines can make real-time response during the operation, but the control program is difficult to design because of lack of theoretical model. Based on the mathematical analysis of finite state machine, we found that the finite state machine can help design a master control program state transition model. Its characteristic is that in different operation stages, the corresponding running state occupies the control initiatives. The model was successfully applied in the "research and development project of automatic bagging machine". The results show that the application of the finite state machine theory in the master control system can greatly improve the degree of automation and operation stability of the machine, with clearer relationship between the transfer of states and conditions.

Keywords：finite state machine; PLC; master control program; transfer of states; bagging machine

[收稿日期]2015-02-26

[作者简介]鲁梦昆(1989-)， 男， 湖北孝感人，湖北工业大学硕士研究生，研究方向为精密仪器及机械

[通讯作者]何涛(1964-)，男，湖北鄂州人，湖北工业大学教授，研究方向为虚拟仪器及自动控制技术

[文章编号]1003-4684(2016)02-0027-04

[中图分类号]TP273.1

[文献标识码]：A