基于蒙特卡洛算法的精度试验序贯检验方案设计

李志刚

（92941部队94分队，葫芦岛　125000）



基于蒙特卡洛算法的精度试验序贯检验方案设计

李志刚

（92941部队94分队，葫芦岛125000）

摘要：介绍了武器系统精度试验的序贯检验方案，分析了方案设计时在设计计算中存在的问题并提出了采用蒙特卡洛法进行序贯检验的方案。实例表明运用蒙特卡洛随机仿真模拟方法进行序贯检验方案设计，能够得到满足设计风险的检验方案，可以作为序贯检验方案设计的有效手段。

关键词：精度试验；序贯检验；蒙特卡洛法

序贯检验方案是武器系统精度试验等领域常用的检验方法之一，在序贯检验方案的设计中，由于目标函数不能用数学表达式写出［1］，使得传统的采取离散的方法进行方案设计出现了问题：设计计算复杂而且参数精度不高，导致检验风险拟合不够好。蒙特卡洛（Monte-Carlo）方法，是对随机变量进行统计试验，用数值方法求取问题的近似解。这种方法是通过概率分布或概率密度进行求解，是在全概率的基础上进行的，因而其模拟结果是精确的。蒙特卡洛法的求解过程是：第一，建立问题的概率模型或随机过程，让其参数与问题的解相等；第二，通过观察或抽样，对模型或过程需要求取的参数统计特征进行计算；第三，得到所求参数的近似解，并且可以用估值的标准误差描述解的精度，即通过所谓“抽签试验”来确定包含大量随机因素的物理过程的概率特性。因此，通过蒙特卡洛法，可以解决精度试验序贯检验方案设计的问题。

1　序贯检验基本思想

序贯检验是Wald A在二次大战期间创立的，之后得到了快速发展并被各个领域广泛应用。序贯检验方法的样本容量在试验前并不事先约定，在试验时，根据试验过程中的观察值，通过统计推断作出判断，从而决定是否继续试验；如果继续试验，则根据整个试验的观察值（包含前期所有试验的观察值），通过统计推断进行判断，直至能够得出试验结论为止。对于武器系统精度试验而言，其序贯检验就是按上述方法，一次一次地进行试验和判断，直到能够得出结论，可以确定结束试验为止。因此，整个系统精度序贯检验的样本量是随机的，最终的样本量是在试验结束时才知道结果，而在试验过程中，相当于划分了一个既不能接收也不能拒收的继续试验区，子样落在这一区域时不能够做出接收和拒收的判断，因而要选择继续试验，这样就能避免固定样本条件下微小的子样变化可能导致不同决策结果的弊端。由于系统精度序贯检验是在试验进行过程中，通过对整个过程的统计做出推断，这样所有试验信息都得到了有效利用，因此序贯检验最大的好处还在于有可能缩小试验次数。

武器系统射击精度即射击命中问题，一般服从二项分布，因此有统计假设：

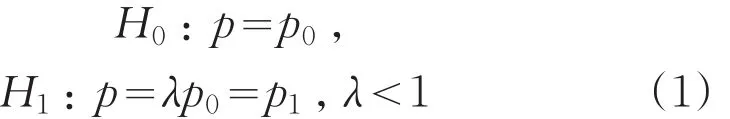
式中，p0为命中概率设计指标，p1为使用方不希望但能接受的最低命中概率值［2］。

在进行武器系统精度试验序贯检验时，选择生产和使用方双方风险分别为α、β，选择与α和β有关的两个常数A和B，A和B的关系需满足0＜A＜1＜B，然后对武器系统精度涉及的随机变量试验，在每次试验（例如第n次试验）以后，求得似然比On［3］，若A＜On＜B，则选择继续试验；若On≤A，则选择接收假设H0，试验终止；若On≥B，则选择拒绝假设H0，此时同样要结束试验［4，5］。A、B的取值可以由以下不等式确定［6］：

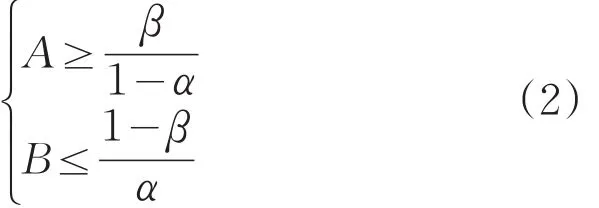
式（2）仅仅表述了A、B的取值范围，并不是A、B的确切表达式。A.Wald已证明A、B存在确定的值，尽管选择的A、B值需要与α、β有关，但想用α、β表示其确切值是困难的，因此，A.Wald建议用下式代替A、B取值：

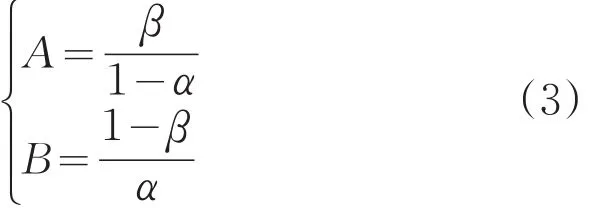
这样选取的是A、B的近似值，其结果是继续试验范围扩大了，而且还会导致实际试验风险α*≤α、β*≤β，并有可能增加实际试验数。所以，这样的选择不符合武器系统精度的试验设计要求。因此，为了得到A、B的“真值”，采用通过蒙特卡洛法进行随机模拟的方法，寻找A、B“真值”，使试验双方实际风险α*=α、β*=β，并尽可能减少实际试验次数。

序贯检验主要解决三个方面问题：确定常数A、B；评价检验结果的好坏；确定平均试验次数［7，8］。

2　序贯检验方案设计模型的确定

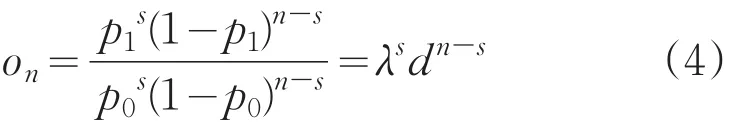
选择生产和使用方双方风险分别为α0、β0。武器系统精度试验序贯检验方案如图1所示。

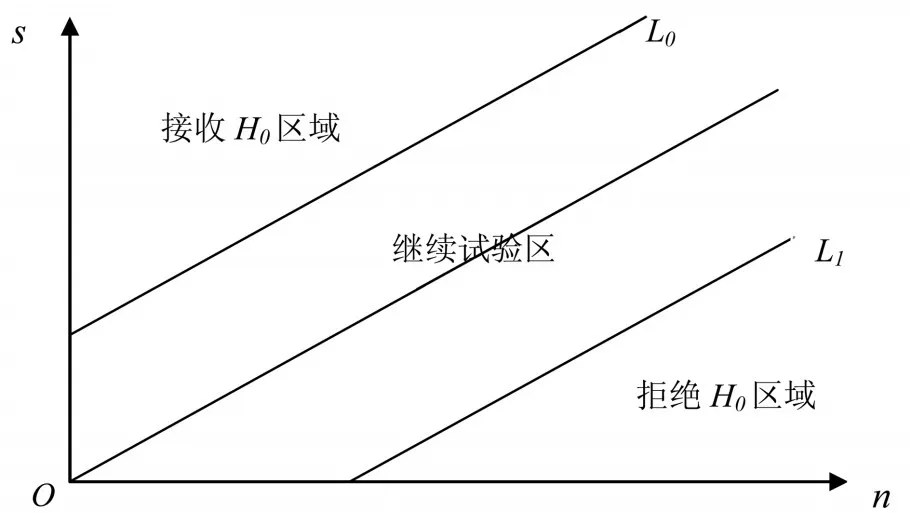
图1　武器系统精度序贯检验方案

试验过程中，若满足On≤A，则接收H0，其临界线L0为：

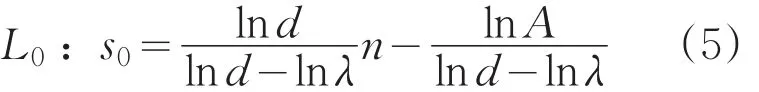
同样，若On≥B，则拒绝H0，其临界线L1为：

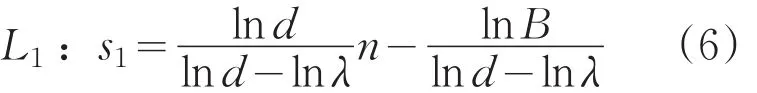
如果在武器系统精度试验序贯检验方案中，实际风险为α*、β*，那么蒙特卡洛法随机模拟的目的，是寻找A、B的值，使α*=α0、β*=β0。根据上面的叙述，序贯检验设计模型如下：

设计变量：A、B，其取值范围为［9］：

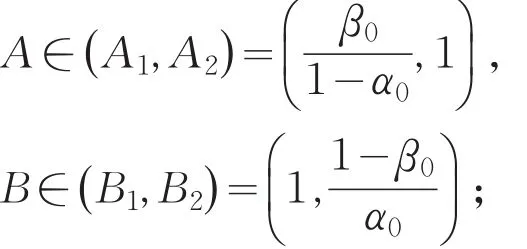
目标函数

式（7）中，ε是足够小的正数。

优化设计结果为：A*、B*、α*、β*及平均试验数n*。

3　序贯检验方案设计的寻优方法

在序贯检验中，α*、β*是关于A、B的函数，即：

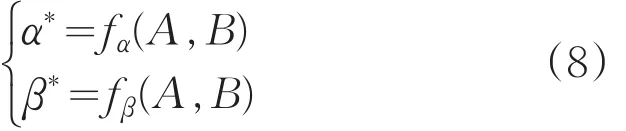
显然，若果想压缩继续试验区，就相当于要增大A，减小B，这样会导致α*、β*均增大，以上表述可表示为：（A↑，B↓）→（α*↑，β*↑）

同样，

扩展继续试验区：（A↓，B↑）→（α*↓，β*↓）；

上移继续试验区：（A↓，B↓）→（α*↑，β*↓）；

下移继续试验区：（A↑，B↑）→（α*↓，β*↑）。

于是，得到如下寻优准则：

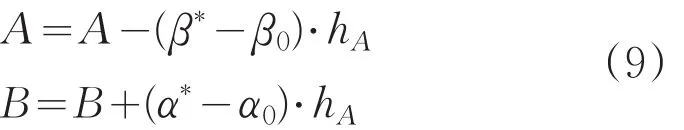
式中：hA，hB为优化步长。

式（9）给出了武器系统精度试验序贯检验的自动寻优过程，它可以按照试验双方设计风险需求，通过调整A、B的值来改善实际风险α*、β*，进而满足武器系统精度试验设计要求。在精度试验序贯检验的方案设计中，对式（9）的变量A、B还需进行归一处理。令归一处理的A、B对应值分别为xA、xB，则xA、xB的变化区间均为（0，1），其计算公式如下：

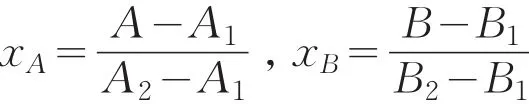
于是，式（9）式改写为：

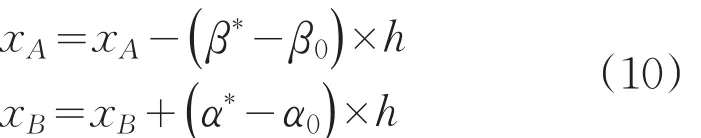
A、B用下式还原：

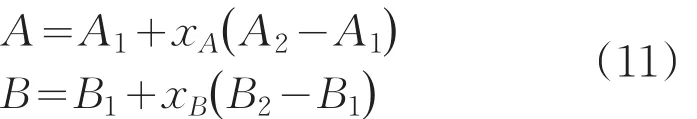
4　序贯检验方案设计的随机仿真模拟

4.1蒙特卡洛随机仿真模拟方法

在序贯检验方案的设计中，由于目标函数不能用数学表达式写出，因此通过蒙特卡洛随机仿真模拟对其进行计算，用迭代法实现具体设计，其算法框图如图2所示。

在图2的随机仿真模拟中，精度试验序贯检验的双方实际风险α*、β*计算步骤如下：

a.成败型二项分布的模拟抽样

1）产生随机数r～U（0，1）；

2）若r≤p，令x=1，反之x=0；

得到的x为成败型二项分布的抽样结果。

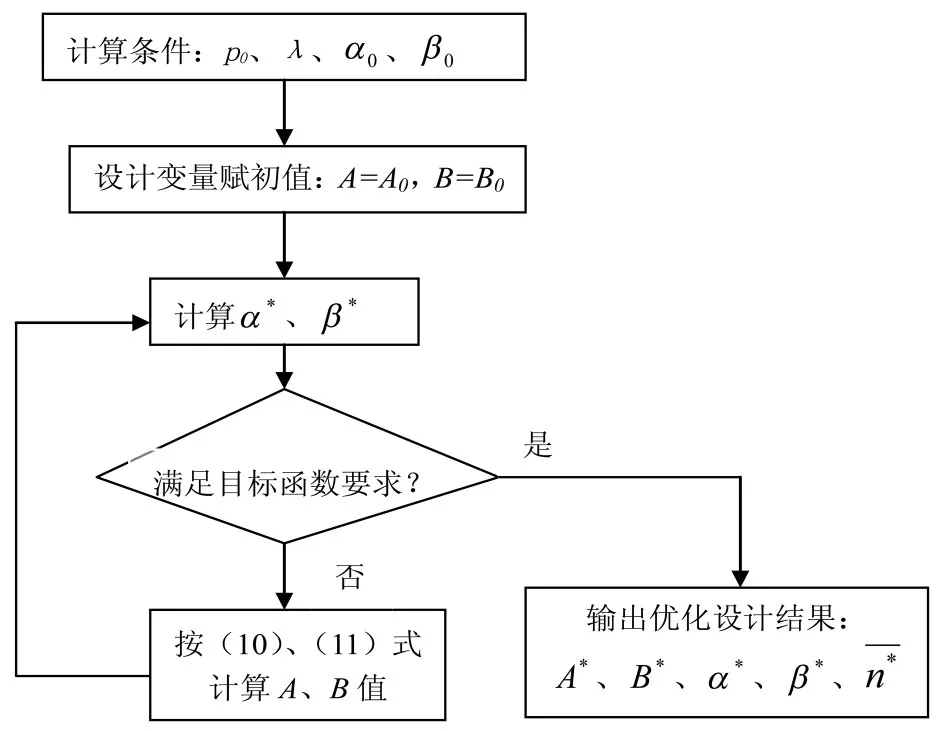
图2　序贯检验算法框图

b.对一次序贯检验进行随机模拟

1）对H0假设进行抽样，令P=P0，按A、B的给定值计算，框图图3所示。

2）把P0换为P1，按1）的方法，对H1假设按A、B给定值随机模拟，计算结果为n1、x1、SH1。

以上两个步骤是武器系统精度序贯检验的一次随机模拟过程。

c.计算双方实际风险α*、β*和试验的平均试验数

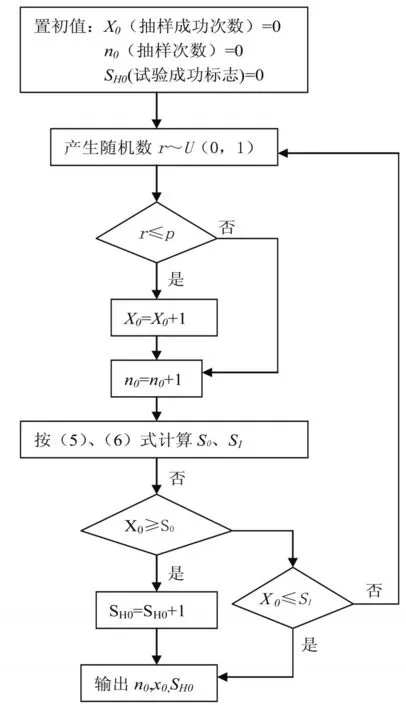
图3　一次序贯试验（P=P0）随机模拟计算框图

表1　检验方案随机仿真模拟结果

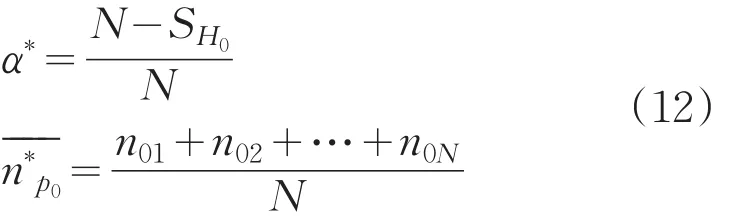
同样，记：P=P1时，N次随机模拟中采纳H0的次数为SH1，则拒绝H0次数为N-SH1，并得到试验样本数nli，（i =1，2，…，N），有：

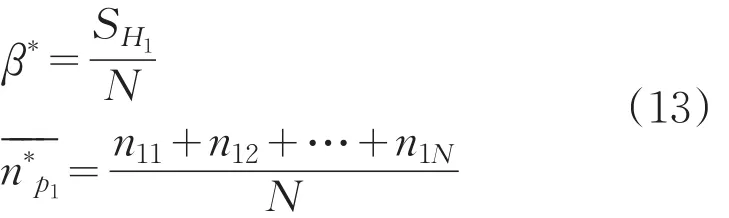
对于随机模拟次数N的取值，在对事件A发生的概率P进行随机模拟时，为了使概率误差不大于ε，随机模拟次数N一般不应少于：

式中，θ可以取一个预先的粗略估计值。在武器系统精度序贯检验中，事件A是指计算α*、β*，式14中的θ可用α0或β0代替。

4.2仿真实例

假定命中概率设计指标p0为0.5，鉴别比λ为0.5或0.67，双方风险α0、β0选取相同风险0.2或0.3进行了二组仿真模拟；假定命中概率设计指标p0为0.5，双方风险α0、β0选取相同风险0.2或0.3进行了一组仿真模拟。在仿真模拟中，选取的风险计算误差ε为0.02，模拟次数N取5000，仿真模拟结果见表1。

5　结论

运用Monte—Carlo方法进行随机仿真模拟，通过模拟可以制定给定条件下的试验方案，这样在试验过程中每进行一次试验就可以迅速判断试验是否继续进行，及时给出接收还是拒收的结论；通过仿真模拟方案试验，预期的实际风险与设计风险拟合较好，能够得出满足设计风险的试验结论，可以作为方案制定的有效手段。

参考文献

［1］林海，高坤.基于加权蒙特卡洛法的新型攻坚弹射击命中概率［J］.四川兵工学报，2010，31（10）：19-21.

［2］吴翊，李永乐，胡庆军.应用数理统计［M］.长沙：国防科技大学出版社，1995.

［3］唐雪梅，张金槐，邵凤昌.武器装备小子样试验分析与评估［M］.北京：国防工业出版社，2001.

［4］黄守训.舰炮武器系统试验与鉴定［M］.北京：国防工业出版社，2002.

［5］杨榜林，岳全发.军事装备试验学［M］.北京：国防工业出版社，2002.

［6］张金槐，唐雪梅.Bayes方法［M］.长沙：国防科技大学出版社，1989.

［7］刘奎勇，典守训，郝瑞云.序贯分析法在舰炮武器试验中的应用［J］.火力与指挥控制，2004，29（1）：98-102.

［8］孙晓峰，赵喜春.导弹试验中序贯检验及序贯截尾检验方案的优化设计［J］.战术导弹技术，2001（1）：9-16.

［9］曲宝忠，孙晓峰.海军战术导弹试验与鉴定［M］.北京：国防工业出版社，2005.

Design of Sequential Inspection Scheme for Precision Test Based on Monte-Carlo Method

LI Zhigang
（Unit 94，No. 92941 Troops of PLA，Huludao 125001）

Abstract：Introduces sequential inspection scheme of weapon system precision test，analyzes the problems existing in the design and Monte Carlo method is presented.Examples show that using Monte Carlo stochastic simulation method for sequential inspection scheme design，can meet the design risk for inspection plan，can be used as an effective means of sequential inspection scheme.

Key words：precision test；sequential inspection；Monte-Carlo method

中图分类号：E911

文献标识码：A

文章编号：1672-9870（2016）02-0086-04

收稿日期：2015-09-01

作者简介：李志刚（1971-），男，硕士，高级工程师，E-mail：1106915758@qq.com