基于形状因子的辐射地板传热量计算等效热阻模型

吴小舟+赵加宁+王沣浩

摘 要：对辐射地板传热过程进行分析，提出了基于形状因子的辐射地板传热量计算等效热阻模型.为了验证简化模型的合理性，采用数值模拟计算结果进行验证，并与标准手册中采用的简化模型计算结果进行对比分析.结果表明，当管间距变化范围为50～250 mm，换热管上端填充层厚度变化范围为25～65 mm及热水平均温度变化范围为25～45 ℃时，ISO标准幂函数计算模型、ASHRAE手册平面肋片模型及地暖设计手册等效热阻模型计算结果与数值模拟计算结果相对误差均较大，最大分别为20.2%，30.4%和22.8%，而本文提出的基于形状因子的等效热阻模型计算结果与数值模拟计算结果相对误差较小，最大不超过3%；当管间距变化范围为50～200 mm，换热管上端填充层厚度变化范围为15～55 mm及冷水平均温度变化范围为10～20 ℃时，ISO标准幂函数计算模型、ASHRAE手册平面肋片模型及地暖设计手册等效热阻模型计算结果与数值模拟计算结果相对误差也均较大，最大分别为80.1%，17.7%和16.8%，而本文提出的基于形状因子的等效热阻模型计算结果与数值模拟计算结果相对误差较小，最大不超过2%.

关键词：辐射地板；传热量计算；等效热阻模型；形状因子

中图分类号：TU833.1 文献标识码：A

文章编号：1674-2974（2016）05-0137-07

Abstract：An equivalent thermal resistance model for the heat transfer calculation of radiant floor based on shape factor was developed in this study. The proposed model was verified by numerical simulation， and compared with the data from the universal single power function of ISO standard， the fin model in ASHARE handbook， and the equivalent thermal resistance model in design handbook. The heat transfers obtained by the numerical simulation disagreed significantly with the existing methods including the universal single power function of ISO standard， the fin model in ASHARE handbook， and the equivalent thermal resistance model in design handbook. The maximum error rates were 20.2 %， 30.4 %， and 22.8 %， respectively， when the tube space ranges from 50 to 250 mm， the thickness of fill layer above pipe ranges from 25 to 65 mm， and the average hot water temperature ranges from 25 to 45 ℃. On the other hand， the maximum difference of the heat transfer predictions between the proposed model and the simulation software was less than 3%. When the tube space ranges from 50 to 200 mm， the thickness of fill layer above pipe ranges from 15 to 55 mm， and the average cold water temperature ranges from 10 to 20 ℃， the maximum error rates of the heat transfer predictions between the numerical simulation and the existing methods were 80.1 %， 17.7 %， and 16.8 %. On the other hand， the heat transfer predicted by the proposed model showed less than 2 % of difference from that of the numerical simulation.

Key words：radiant floor； heat transfer calculation； equivalent thermal resistance model； shape factor

辐射地板供暖供冷系统不仅具有较高热舒适性，而且能够显著地降低建筑运行能耗，在公共建筑及住宅中得到广泛的应用[1-3].辐射地板传热量计算模型是辐射地板供暖供冷系统设计和运行控制的关键，因此国内外学者对辐射地板传热量计算模型进行了大量的研究，并提出了很多模型.根据辐射地板传热过程描述的差异，这些模型可以分为3类：解析模型[4-6]、数值模拟模型[7-9]和简化模型[10-12].

解析模型结构相对复杂，不便于工程师及设计师理解应用.而数值模拟模型仅能得到分散的结果，由于辐射地板组成部分及其特性参数可选择的组合较多，导致数值模拟工作量相当大，很难包括所有的组合.因此，结构相对简单及计算时间相对较少的简化模型被广泛应用于辐射地板设计手册及标准中，如ISO标准中的幂函数计算模型[13]、ASHRAE手册中的平面肋片模型[14]及地暖设计手册中的等效热阻模型[15]等.但这些简化模型均存在一定问题，计算精度较低或者使用不方便.如ISO标准幂函数计算模型需要查表二次计算，过程比较繁琐；ASHRAE手册平面肋片模型忽略了地板垂直方向的传热，只考虑水平方向的传热，可能会引起较大的计算误差；地暖设计手册等效热阻模型形式过于简单，计算缺乏理论依据.

本文通过对辐射地板传热过程进行分析，提出计算精度较高且结构相对简单的辐射地板传热量计算简化模型，并与数值模拟模型及标准手册中采用的模型计算结果进行对比分析，为辐射地板供暖供冷系统的设计及运行控制提供理论方法.

1 辐射地板供暖供冷系统传热量计算模型

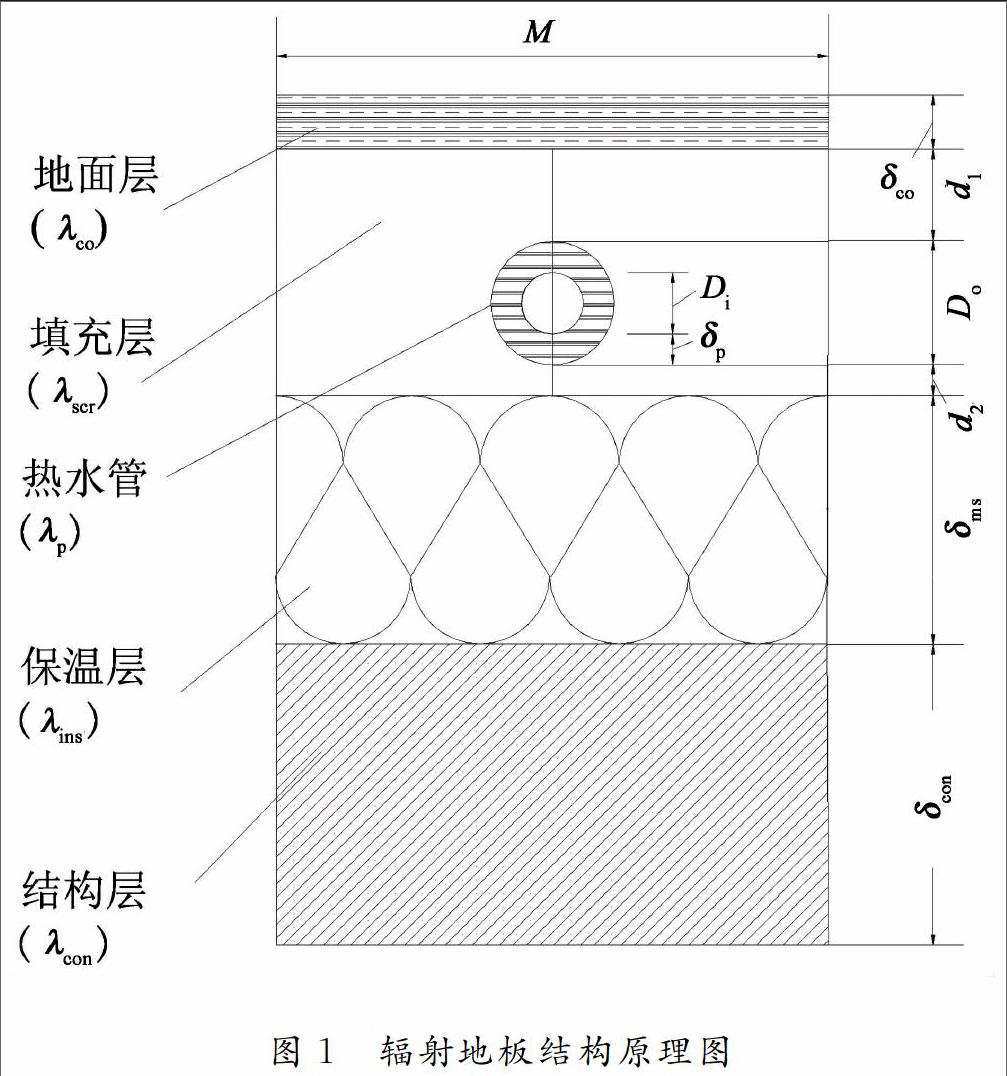
辐射地板供暖供冷系统是将换热管埋设于建筑围护结构（楼板）中的供暖供冷系统，其结构原理如图1所示.

如图1所示，辐射地板主要由地面层、填充层、换热管、保温层和结构层组成.其中λco为地面层的导热系数；λscr为填充层的导热系数；λp为换热管的导热系数；λins为保温层的导热系数；λcon为结构层的导热系数；δco为地面层的厚度；δp为换热管的厚度；δins为保温层的厚度；δcon为结构层的厚度；M为换热管间距；Do为换热管外径；Di为换热管内径；d1为换热管上端的填充层厚度；d2为换热管下端的填充层厚度.

1.1 基于形状因子的等效热阻模型

由图1可知，辐射地板传热过程为：热（冷）水以对流换热方式把热（冷）量传递给管内壁，然后管内壁以导热方式把热（冷）量传递到管外壁，之后管外壁以导热方式通过填充层、保温层或结构层向地板表面传热，最后地板上或下表面以对流与辐射传热方式把热（冷）量传递到室内.

对于辐射地板供暖供冷系统，其传热量的计算难点主要在于计算管外壁面与填充层外壁面之间的导热量.这主要是由于辐射地板中与管外壁接触的填充层部分形状比较复杂，温度及热流密度在二个坐标方向上都是变化的，如此采用分析法求解计算通常相当麻烦和困难.

随着建筑节能技术的不断发展，辐射供暖供冷系统热（冷）媒温度与室内温度相差较小，此时管外壁面与填充层外壁面表面温度可视为均匀分布的，即两者均可作为等温界面.如此管外壁面与填充层外壁面之间的导热量计算可以采用基于形状因子的半无限大物体与其平行的圆管排之间（如图2所示）导热计算公式[16]，其形状因子如式（1）所示.

基于上述分析，本文提出了基于形状因子的辐射地板传热量计算等效热阻模型，其地板上表面传热量计算式如式（2）所示.

辐射地板填充层中的圆排管如图3所示，其填充层等效热阻可视为图2中所述热阻的2倍，因此其形状因子可如式（5）所示.

1.2 数值模拟计算模型

上节通过对辐射地板传热过程进行分析，提出了基于形状因子的辐射地板传热量计算等效热阻模型.为了验证简化模型的合理性，本文将采用与数值模拟计算结果进行对比的方式.这主要是由于辐射地板传热量的数值模拟计算结果可信度较高，相关计算结果已被辐射供暖供冷标准采纳[13].

1.2.1 辐射地板物理模型

相对管间地板温差传热，忽略地板轴向的温差传热能得到足够的计算精度，辐射地板三维导热问题一般可以简化为二维导热问题，如图4所示.

1.2.2 辐射地板数学模型

假设各层材料为各向同性，互相紧密接触，忽略接触热阻，则描述该计算单元的二维稳态导热微分方程式如式（10）所示：

1.2.3 定解条件

1）单元对称边界

对每一个计算单元对称温度场边界有：

2）地板上表面边界条件

地板上表面以对流换热和辐射换热两种方式向房间传热，将对流换热系数和辐射换热系数综合成一个换热系数，如式（12）所示：

3）地板下表面边界条件

地板下表面也是以对流换热和辐射换热两种方式向房间传热，将对流换热系数和辐射换热系数综合成一个换热系数，如式（13）所示：

二维稳态导热微分方程组边界条件复杂，分析求解困难，一般都采用数值求解.HEAT2软件采用有限差分法求解二维稳态导热问题，具有计算精度较高、耗时较短等优点，目前已被辐射供暖供冷国际标准ISO 11855采用[13].因此，本文采用HEAT2软件对上述导热微分方程进行求解计算[17].

2 结果与分析

根据国际标准ISO 11855[13]，典型辐射地板供暖供冷系统结构及传热参数如表1所示.

为了将本文提出的基于形状因子的等效热阻模型与数值模拟计算模型及目前标准规范及手册中采用的模型计算结果进行对比分析，以下将分别采用数值模拟计算模型、ISO标准幂函数计算模型、ASHRAE手册平面肋片模型及地暖设计手册等效热阻模型计算不同工况下辐射地板传热量.

2.1 辐射供暖传热量计算结果与分析

当管间距变化范围为50～250 mm，换热管上端填充层厚度变化范围为25～65 mm及热水平均温度变化范围为25～45 ℃时，不同辐射地板供暖传热量各计算方法的计算结果如表2～表4所示.

由表2知，当换热管上端填充层厚度为 45 mm，热水平均温度为35 ℃及管间距变化范围为50～250 mm时，管间距的变化对ISO标准幂函数计算模型、ASHRAE手册平面肋片模型及地暖设计手册等效热阻模型结果影响较大，这些方法的计算结果与数值模拟计算结果的相对误差基本都超过5%，最大达到30%.而管间距的变化对基于形状因子的热阻模型计算结果影响较小，与数值模拟计算结果的相对误差最大不超过3%.

由表3可知，当管间距为150 mm，热水平均温度为35 ℃及换热管上端填充层厚度变化范围为25～65 mm时，换热管上端填充层厚度的变化对ISO标准幂函数计算模型、ASHRAE手册平面肋片模型及地暖设计手册等效热阻模型结果影响较大，这些方法的计算结果与数值模拟计算结果的相对误差都超过5%，最大达到20%.而换热管上端填充层厚度的变化对基于形状因子的热阻模型计算结果影响较小，与数值模拟计算结果的相对误差最大不超过3%.

由表4可知，当管间距为150 mm、换热管上端填充层厚度为45 mm及热水平均温度变化范围为25～45 ℃时，热水平均温度的变化 对ASHRAE手册平面肋片模型及地暖设计手册等效热阻模型结果影响较大，这些方法的计算结果与数值模拟计算结果的相对误差都超过5%，最大达到17%.而换热管上端填充层厚度的变化对基于形状因子的热阻模型及ISO标准幂函数计算模型计算结果影响较小，与数值模拟计算结果的相对误差最大不超过3%.

2.2 辐射地板供冷传热量计算结果与分析

当管间距变化范围为50～200 mm，换热管上端填充层厚度变化范围为15～55 mm及冷水平均温度变化范围为10～20 ℃时，不同辐射地板供冷传热量各计算方法的计算结果如表5～表7所示.

由表5知，当换热管上端填充层厚度为35 mm，冷水平均温度为15 ℃及管间距变化范围为50～200 mm时，管间距的变化对ISO标准幂函数计算模型、ASHRAE手册平面肋片模型及地暖设计手册等效热阻模型结果影响较大，这些方法的计算结果与数值模拟计算结果的相对误差基本都超过5%，最大达到50%.而管间距的变化对基于形状因子的热阻模型计算结果影响较小，与数值模拟计算结果的相对误差最大不超过2%.

由表6可知，当管间距为100 mm，冷水平均温度为15 ℃及换热管上端填充层厚度变化范围为15～55 mm时，换热管上端填充层厚度的变化对ISO标准幂函数计算模型、ASHRAE手册平面肋片模型及地暖设计手册等效热阻模型结果影响较大，这些方法的计算结果与数值模拟计算结果的相对误差都超过5%，最大达到80%.而换热管上端填充层厚度的变化对基于形状因子的热阻模型计算结果影响较小，与数值模拟计算结果的相对误差最大不超过2%.

由表7可知，当管间距等于100 mm，换热管上端填充层厚度等于35 mm及冷水平均温度变化范围为10～20 ℃时，冷水平均温度的变化对ASHRAE手册平面肋片模型及地暖设计手册等效热阻模型结果影响较大，这些方法的计算结果与数值模拟计算结果的相对误差都超过5%，最大达到44%.而换热管上端填充层厚度的变化对基于形状因子的等效热阻模型及ISO标准幂函数计算模型计算结果影响较小，与数值模拟计算结果的相对误差最大不超过2%.

对比表2～4及表5～7可知，本文提出的基于形状因子的等效热阻模型在供冷工况下的计算误差明显小于供热工况.这主要是因为供冷工况相比供热工况，供水平均温度更接近于室内温度，导致管外壁面与填充层外壁面表面温度分布相对更均匀，与模型假设一致，因此模型计算误差相对较小.

根据本文的计算结果可得到本文提出的基于形状因子的等效热阻模型与其他简化模型的对比结果，如表8所示.

由表8可知，本文提出的基于形状因子的等效热阻模型计算精度较高，使用范围较广.一般而言，换热管上端填充层厚度均大于水管的半径，因此本文提出的基于形状因子的等效热阻模型可用于常规的辐射地板供暖供冷系统设计及运行调节.

本文提出的基于形状因子的等效热阻模型使用过程与其他简化模型基本一致.已知房间冷热负荷及供回水温度条件下，通过调整管间距及换热管上端填充层厚度等使设计的辐射地板供热供冷量等于或略大于房间冷热负荷，此时的管间距及换热管上端填充层厚度等即为辐射地板设计参数.

3 结 论

本文通过对辐射地板传热过程进行分析，提出了合理的基于形状因子的辐射地板传热量计算等效热阻模型，并与标准手册中采用的模型计算结果进行对比分析，得到以下结论：

1）ISO标准幂函数计算模型、ASHRAE手册平面肋片模型及地暖设计手册等效热阻模型的计算精度均较低；

2）本文提出的基于形状因子的等效热阻模型不仅计算精度较高，而且形式相对简单.

参考文献

[1] RICHARD W， CHAPMAN K. Radiant heating and cooling handbook [M]. New York ：McGraw Hill Professional， 2002：12-15.

[2] JAN B， OLESEN B W， KIM K W. Low temperature heating and high temperature cooling[M]. Brussets： REHVA， 2009：24-28.

[3] ROBERT B， OLESEN B W， KIM K W. History of radiant heating &cooling systems[J]. ASHRAE Journal， 2010， 52（1）：26-31.

[5] LU X ， TERVOLA P， Transient heat conduction in the composite slab-analytical method[J]. Journal of Physics A： Mathematical and General， 2005， 38 （1） ：81-86.

[6] ABDELAZIZ L. Development of a radiant heating and cooling model for building energy simulation software[J]. Building and Environment， 2004， 39 （4）： 421-431.

[7] 李安邦，徐新华.内嵌管式辐射地板的频域热特性分析[J].湖南大学学报：自然科学版，2015，42（1）：115-119.

[8] SILVANA F L， FILIPPN C ， LESINO G. Transient simulation of a storage floor with a heating/cooling parallel pipe system[J]. Building Simulation， 2010， 3 （2） ：105-115.

[9] JIN Xin， ZHANG Xiao-song. Numerical simulation of radiant floor cooling system： the effects of thermal resistance of pipe and water velocity on the performance[J]. Building and Environment ， 2010，45 （11） ：2545-2552.

[10]LIU Yan-feng， WANG Deng-jia ， LIU Jia-ping. Study on heat transfer process for in-slab heating floor[J]. Building and Environment， 2012， 54（10）： 77-85.

[11]ZHANG Lun， LIU Xiao-hua ， JIANG Yi. Simplified calculation for cooling/heating capacity， surface temperature distribution of radiant floor[J]. Energy and Buildings， 2012， 55（12）：397-404.

[12]LI， Qing-qing. Simplified thermal calculation method for floor structure in radiant floor cooling system[J]. Energy and Buildings， 2014， 74（7）： 182-190.

[13]ISO/DIS 11855-2 Building environment design-design， construction and operation of radiant heating and cooling systems-part 2： determination of the design heating and cooling capacity[S]. Brussels：International Organization for Standardization，2010：7-9.

[14]HANDBOOK A. HVAC systems and equipment[M]. Atlanta， GA： American Society of Heating， Refrigerating and Air Conditioning Engineers， 2011：11-13.

[15]鲁翠.地板采暖设计施工手册[M].北京：中国电力出版社，2009：16-19.

[16]钱滨江，伍贻文，常加芳，等.简明传热学手册[M].北京：高等教育出版社，1983：22-24.

[17]BLOMBERG T. Heat 2-A heat transfer PC-program： manual for heat2[D]. Lund：Department of Building Physics，University，Lund， 1991： 22-25.