动态网络最短路径射线追踪算法中向后追踪方法的改进

卢江波+方志

摘 要：动态网络最短路径射线追踪算法中的向后追踪方法能够解决线性走时插值算法（LTI）向后追踪过程不稳定的问题，但是其计算效率较低.综合利用节点次级源的位置信息以及波的传播规律，提出了改进方法，排除了动态网络最短路径射线追踪算法向后追踪过程中存在的大量冗余计算.数值算例表明，改进的向后追踪方法具有较高的计算效率，是动态网络最短路径射线追踪算法中向后追踪方法的几倍至几十倍；若将改进后的向后追踪方法应用于动态网络最短路径射线追踪改进算法，则该算法的计算效率将提高一倍左右.

关键词：射线追踪；线性走时插值；向后追踪方法；计算效率；初至波射线追踪

中图分类号：P631 文献标识码：A

文章编号：1674-2974（2016）05-0106-07

Abstract：The backward tracing method of the shortest path ray tracing algorithm with dynamic networks can solve the unstability problem in the backward tracing procedure of the LTI （Linear Travel-time Interpolation） algorithm， but the computational efficiency of the method is low. This study presented an improved method on backward tracing. According to the location information of the secondary sources for the nodes and the law of wave propagation， a large number of redundancy calculation are excluded in the backward tracing of the dynamic networks tracing algorithm. The numerical examples show that the improved method exhibits the higher computational efficiency. The calculation efficiency of the improved method is several times that of the backward tracing method of the dynamic networks tracing algorithm. When the improved method is applied to the improved algorithm of the shortest path ray tracing with dynamic networks， the computational efficiency of the algorithm can be increased by about 100 %.

Key words：ray tracing； linear traveltime interpolation； improved algorithm； backward tracing； computational efficiency；first arrival ray tracing

射线追踪技术在地震层析成像以及混凝土超声波射线层析成像等领域具有重要作用.目前常用射线追踪方法主要有两点射线追踪算法（包括试射法以及弯曲法）[[1-3]、有限差分解程函方程法[[4-6]、最短路径法[[7-10]以及LTI（Linear Travel-time Interpolation）射线追踪算法[[11-22]等.其中，LTI射线追踪算法因其计算精度较高、计算速度较快且适用于任意复杂的速度介质模型，在地震层析成像等领域得到了广泛应用.但是LTI原算法[[11]存在两个问题：在向前计算节点最小走时时，不能正确追踪逆向传播的射线，相关节点不能得到正确的最小走时[[16-22]；在向后追踪接收点射线路径时，存在不能正确追踪接收点射线路径的可能，算法的稳定性存在不足.

文献[17-18]将波前扩展方式与LTI算法基本方程相结合，提出了动态网络最短路径射线追踪算法，该算法在向前计算各节点的最小走时时，从震源点开始，采用波前扩展的方式逐点计算各个节点上的最小走时，改变了LTI原算法的计算方式，确保各节点能得到最小走时；在向后追踪接收点射线路径时，基于互换原理考虑了接收点所有可能的射线路径，确保算法能正确追踪接收点的射线路径.

动态网络最短路径射线追踪算法虽然能够解决LTI原算法存在的两个问题，但是其计算效率偏低.文献[22]基于波的传播规律提出了动态网络最短路径射线追踪改进算法，改进并提高了动态网络最短路径射线追踪算法向前计算节点最小走时这一步骤的计算效率，但是，该改进方法的向后追踪方法仍然采用动态网络最短路径射线追踪算法中的方法，计算效率依然偏低.

针对动态网络最短路径射线追踪算法中的向后追踪方法存在计算效率低的问题，本文提出了改进方法.首先，在向前计算节点最小走时这一步骤中，不仅计算各节点的最小走时，而且还记录各节点次级源的位置；然后，在向后追踪接收点的射线路径时，利用各节点次级源的位置信息以及波的传播规律对算法进行改进，降低算法的计算量，提高算法的计算效率.

1 LTI算法基本方程的推导及接收点

文献[8]给出了最短路径射线追踪算法中次级源的确定方法，考虑到LTI算法中的射线可通过单元边界上任意点进行传播，这与最短路径射线追踪算法中射线只能通过节点进行传播不同，因此最短路径射线追踪算法中次级源的确定方法不完全适合LTI算法.为了更好地描述本文提出的改进方法，将LTI算法中次级源的确定方法规定如下：通过接收点所在单元各节段（不包括接收点所在节段）可得到多个接收点走时，其中走时最小值对应的点即为接收点的次级源，如果走时最小值对应多个点，取距离接收点最近的点作为接收点的次级源.如图1所示，若接收点C通过AB节段D点得到的走时小于通过单元其它节段得到的走时，那么D点即为接收点C的次级源.

2 LTI原始算法向后追踪过程存在的问题及动态网络最短路径射线追踪算法存在的不足及改进

LTI原始算法在向后追踪接收点射线路径时，首先逐点计算接收点所在单元中各节点走时与节点至接收点的走时之和，然后选出最小的走时之和以及相应的节点，最后将单元中包含该节点的节段作为接收点次级源的可能区域[[11].事实上，接收点的次级源并不一定在这些节段中.此外，LTI原算法在确定接收点次级源的可能区域时，并未排除接收点所在的节段，算法可能会陷入无限循环.因为通过接收点所在节段线性插值得到的接收点走时，可能比通过单元其它节段得到的走时更小，那么接收点取最小走时对应的点可能为接收点本身，算法可能会进入无限循环.

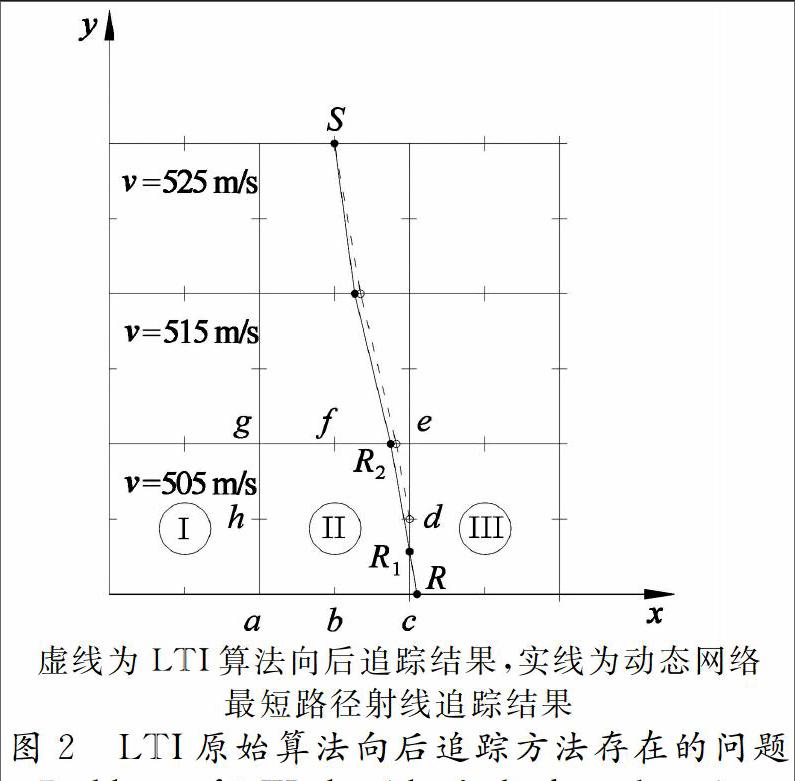
以图2所示模型为例，模型尺寸为3 m×3 m，单元大小为1 m×1 m，单元边界划分为2个节段，模型上层、中层以及下层单元的速度分别为525 m/s，515 m/s和505 m/s，震源S的x，y坐标分别为1.5和3.0，接收点R的x，y坐标分别为2.05和0；图中虚线为采用LTI原始算法中的向后追踪方法得到的射线路径，需要说明的是，计算这条射线路径时，已经排除了接收点的次级源位于接收点所在节段的情况，实线为根据动态网络最短路径射线追踪算法中的向后追踪方法[[17-18]得到的射线路径.

从图2可以看出，在III号单元中，两种方法的计算结果一样，接收点R的次级源均为R1.在II号单元中，对于LTI原始算法的向后追踪方法，首先须确定II号单元中节点走时与节点至接收点R1走时之和最小的节点，经计算确定为d节点，然后确定cd或de节段为接收点R1次级源的可能区域；对于动态网络最短路径射线追踪算法中的向后追踪方法，接收点R1次级源所在区域为ef节段.计算结果表明：通过ef节段计算得到的R1点的走时（T=0.005 416 05 s）要小于通过cd或de节段的走时（T=0.005 422 57 s），接收点R1的次级源不在cd或de节段内.造成这一问题的根源在于：LTI算法假定射线路径可以经过单元边界的任意一点，在向后追踪过程中必须考虑所有可能的射线路径，并根据费马原理选择走时最短的那条路径[[11]，而LTI原始算法的具体追踪方法却没有考虑接收点所在单元所有节段的射线，而是采用了一种“简化”方法确定接收点射线路径或次级源的可能区域，由图2所示模型可以看出，这种“简化”方法存在不足.

此外，在确定接收点次级源时，若不排除接收点所在的节段，那么在计算新接收点R1的次级源时，由于通过节段cd插值得到的走时，比通过ed节段得到的走时小，计算得到的“次级源”为R1本身，程序将陷入无限循环.

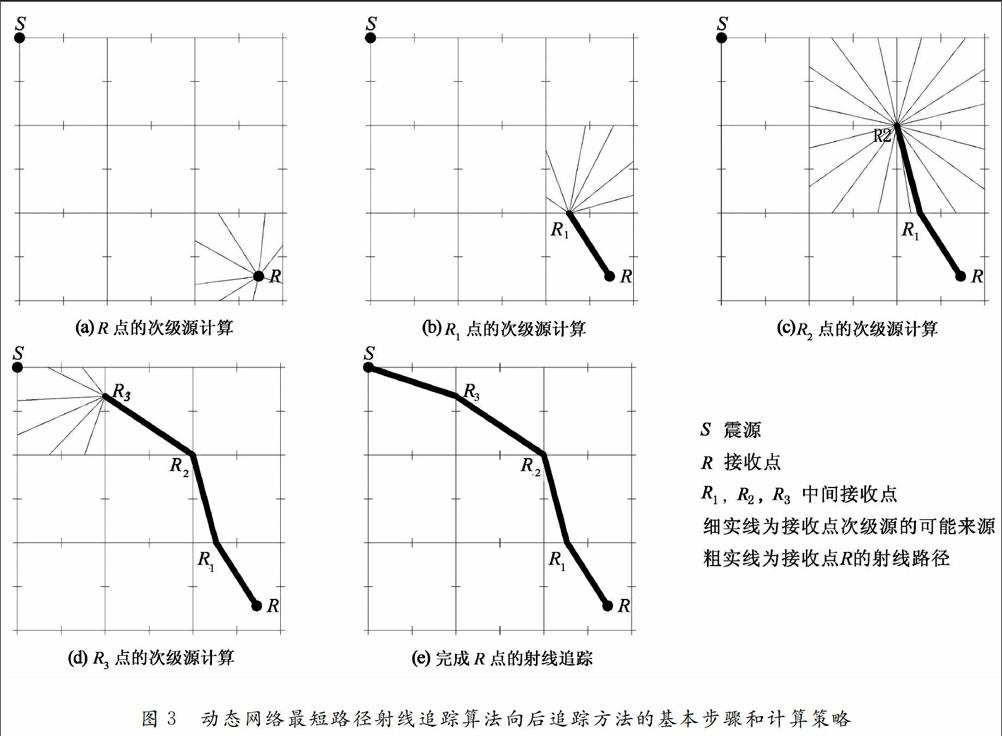
动态网络最短路径射线追踪算法中基于互换原理提出的向后追踪方法[[17-18]，考虑了来自接收点所在单元中除接收点所在节段外所有节段的射线，确保了接收点能得到其次级源.但是，该方法计算量大，计算效率低.为了解决这一问题，本文首先在向前计算节点最小走时的步骤中，建立了一个数组，专门用于记录节点次级源的位置信息.然后利用各节点次级源的位置信息以及波的传播规律对动态网络最短路径射线追踪算法中的向后追踪方法进行改进.现以图3所示模型为例，对该向后追踪方法的基本步骤及计算策略进行说明，同时对向后追踪改进方法进行阐述，改进前后的向后追踪方法及计算策略分别如图3和图4所示.具体步骤和分析如下：

1）首先将接收点分为以下3种情况，然后对不同的情况采用不同的策略求解接收点的次级源：

①接收点位于单元内部，如图3（a）及图4（a）所示的R点.此时利用LTI算法的相关公式计算接收点所在单元各节段至接收点的走时，然后从中选出走时最小值对应的点，如图3（b）及图4（b）中的R1点，这个点就是接收点的次级源.

②接收点位于单元边界上，但是非单元边界上的节点.如图3（b），（d）中的R1和R3点，此时除接收点所在的节段外，单元中的其它节段均要计算从该节段至接收点的最小走时，然后从中选出走时最小值对应的点，如图3（c），（e）中的R2和S点.

事实上，对于接收点位于单元边界但非单元节点的情况，除非该接收点为原始接收点（图3和图4中的R），否则并不需要对接收点进行全方位的计算.可以采取如下两个步骤确定接收点次级源的可能区域.

首先，利用接收点所在节段端点的次级源位置信息确定两个定位点.定位点的确定方法为：若节点端点的次级源不在单元内，或者次级源在单元内但与节点端点处于同一边界，则定位点为节段端点本身，其它情况定位点为节点端点的次级源.如图4（b）所示，接收点R1所在节段的端点为A1和A2，易知接收点R1的次级源位于单元I中，现以端点A1的次级源位置信息为例说明定位点的确定方法，若A1的次级源不在单元I中，比如A1的次级源为单元II中的b点，则由A1的次级源位置信息确定的定位点为A1本身；若A1的次级源与A1处于同一边界，比如次级源位于A1A4或者A1A6边界，则定位点为A1本身；对于其它情况，比如A1的次级源为单元I中的c点，则定位点为A1的次级源c.在图4（b）中，假定A1节点的次级源为A3节点，A2节点的次级源为a1点，则由A1，A2节点的次级源位置信息可以确定两个定位点，分别为A1节点本身以及点a1.

然后沿着单元边界连接两个定位点，其中不包含接收点的那条路径即为接收点次级源的可能区域.如图4（b）所示，沿单元边界连接定位点A1和a1可以得到两条路径：A1A3A4a1和A1A6A7a1，其中路径A1A3A4a1不包含接收点R1，因此确定该路径为接收点次级源的可能区域.

得到次级源的可能区域后，再确定这个区域内的节段，图4（b）中可能区域A1A3A4a1内的节段为A1A3，A3A4，A4A5，计算从这些节段至接收点的最小走时，其中走时最小的点即为接收点的次级源，如图4（c）中的R2.

同理得到图4（d）中R3点的次级源S.

③接收点位于单元边界上，且为单元边界上的节点.如图3（c）中的R2节点，此时需要在R2节点所处的几个单元中执行情况②的计算，如图3（c）.

显然，由于在向前计算节点最小走时的过程中，已经记录了各节点的次级源，因此，在改进方法中，可以直接得到接收点的次级源，如图4（c）.

2）以步骤1）中获得的次级源为新的接收点，重复步骤1），直至新的接收点为震源.

3）依次连接各接收点得到R点的初至波射线路径，如图3（e）和图4（e）所示.

对比图3与图4可以看出，改进后的向后追踪方法计算量明显减少.

3 数值算例

为了对比改进前后向后追踪方法的计算效率，建立了尺寸为2 500 m×600 m的二维模型，如图5所示，其中x值在500～2 000 m之间且y值在200～400 m之间的区域为低速区，速度为500 m/s，其余速度均为4 000 m/s，震源S位于模型上表面的正中间（1 250，0），单元尺寸为5 m×5 m，单元边界划分段数为4，10，20等3种情况，模型下表面的每个单元布置一个接收点，共500个，部分接收点的射线路径如图6所示，分别记录两种向后追踪方法追踪所有接收点的射线路径所耗费的总时间.此外，为了说明向后追踪方法计算效率的提高对整个算法的影响，将改进后的向后追踪方法应用于动态网络最短路径射线追踪改进算法[[22]，然后比较应用改进方法前后动态网络最短路径射线追踪改进算法的总耗时（不包括算法的前处理过程）.计算机CPU主频为3.4 GHz，计算结果如表1所示.

由表1可知，向后追踪改进方法的计算效率较高，是改进前向后追踪方法的几倍至几十倍.并且能将动态网络最短路径射线追踪改进算法的计算效率提高1倍左右.

为验证向后追踪改进方法对复杂模型的有效性，采用向后追踪改进方法对Marmousi速度模型进行射线追踪，其中节点最小走时的计算采用的是动态网络最短路径射线追踪改进算法.模型尺寸为9 192 m×2 904 m，震源S位于模型左上角（0，0），单元尺寸为24 m×24 m，单元边界划分为10段，共设置5个接收点R1～R5，分别位于模型上表面的3 600，4 800 m，6 000 m，7 200 m和8 400 m，射线追踪结果如图7（a）所示，作为对照，本文给出了单元边界划分为30段时最短路径法的射线追踪结果，如图7（b）所示.两种算法下，各接收点根据射线追

踪结果计算的走时如表2所示.计算结果表明，向后追踪改进方法对于复杂的速度模型同样有效.

4 结 论

针对LTI原算法中向后追踪方法存在的无限循环以及可能不能得到正确射线路径的问题，动态网络最短路径射线追踪算法中基于互换原理提出的向后追踪方法能够予以有效的解决.但是该算法存在较多的无效计算.本文根据模型中节点次级源的位置信息以及波的传播规律，提出了改进的向后追踪方法.数值结果表明，改进后的向后追踪方法，其计算效率较之改进前的方法有较大程度的提高；此外，本文提出的向后追踪改进方法能将动态网络最短路径射线追踪改进算法的计算效率提高1倍左右.

参考文献

[1] JULIAN B R，GUBBINS D.Three-dimensional seismic ray tracing[J].J Geophys，1977，43（1/2）：95-113.

[2] 田玥，陈晓非.水平层状介质中的快速两点间射线追踪方法[J]. 地震学报，2005，27（2）：147-154.

[3] XU Tao，ZHANG Zhong-jie，GAO Ergen，et al. Segmentally iterative ray tracing in complex 2D and 3D heteroge-neous block models[J]. Bulletin of the Seismological Society of America， 2010，100（2）： 841-850.

[4] VIDALE J.Finite-difference calculation of travel times[J].Bulletin of the Seismological Society of America， 1988，78（6）： 2062-2076.

[5] QIN Fu-hao， LUO Yi， OLSENl K B， et al. Finite-difference solution of the eikonal equation along expanding wavefronts[J].Geophysics， 1992，57（3）：478-487.

[6] 李振春，刘玉莲，张建磊，等.基于矩形网格的有限差分走时计算方法[J]. 地震学报， 2004，26（6）：644-650.

[7] MOSER T J. Shortest path calculation of seismic rays[J]. Geophysics， 1991，56（1）： 59-67.

[8] 刘洪，孟凡林，李幼铭.计算最小走时和射线路径的界面网全局方法[J].地球物理学报， 1995，38（6）： 823-832.

[9] 赵爱华，徐涛.提高规则网格最短路径方法反射波走时计算精度的走时校正技术[J]. 地球物理学进展， 2012，27（5）：1854-1862.

[10]BAI Chao-yin，HUANG Guo-jiao，ZHAO Rui. 2-D/3-D irregular shortest-path ray tracing for multiple arrivals and its applications[J]. Geophysical Journal International， 2010，183（3）： 1596-1612.

[11]ASAKAWA E，KAWANAKA T. Seismic ray tracing using linear traveltime interpolation[J]. Geophysical Prospecting， 1993，41（1）： 99-111.

[12]赵改善，郝守玲，杨尔皓，等.基于旅行时线性插值的地震射线追踪算法[J].石油物探， 1998，37（2）：14-24.

[13]CARDARELLI E，CERRETO A. Ray tracing in elliptical anisotropic media using the linear traveltime interpolation （LTI） method applied to traveltime seismic tomography[J]. Geophysical Prospecting， 2002，50（1）： 55-72.

[14]聂建新，杨慧珠.地震波旅行时二次/线性联合插值法[J].清华大学学报：自然科学版 ， 2003，43（11）：1495-1498.

NIE Jian-xin， YANG Hui-zhu.Quadratic/linear travel timeinterpolationof seismic ray tracing[J].J Tsinghua Univ ：Sci&Tech， 2003，43（11）：1495-1498.（In Chinese）

[15]ZHANG Jian-zhong， HUANG Yue-qin， SONG Lin-ping，et al.Fast and accurate 3-D ray tracing using bilinear traveltime interpolation and the wave front group marching[J]. Geophysical Journal International， 2011，184（3）： 1327-1340.

[16]黄靓，黄政宇.线性插值射线追踪的改进方法[J]. 湘潭大学自然科学学报， 2002，24（4）： 105-108.

[17]张建中，陈世军，余大祥.最短路径射线追踪方法及其改进[J].地球物理学进展， 2003，18（1）：146-150.

[18]张建中，陈世军，徐初伟.动态网络最短路径射线追踪[J]. 地球物理学报， 2004，47（5）： 899-904.

[19]黄靓.混凝土超声波层析成像的理论方法和试验研究[D]. 长沙： 湖南大学土木工程学院， 2008：33-36.

[20]张东，谢宝莲，杨艳，等.一种改进的线性走时插值射线追踪算法[J]. 地球物理学报， 2009，52（1）： 200-205.

[21]卢江波，方志.线性走时插值射线追踪算法的改进[J].湖南大学学报：自然科学版， 2014，41（1）：39-44.

[22]卢江波，方志.一种线性走时插值射线追踪改进算法[J].地震学报， 2014，36（6）：1089-1100.