条形区域极点配置静态输出反馈可靠控制
徐艺超,王福忠,姚 波
(1.沈阳师范大学 数学与系统科学学院,辽宁 沈阳 110034;2.沈阳工程学院 基础教学部,辽宁 沈阳 110136)
条形区域极点配置静态输出反馈可靠控制
徐艺超1,王福忠2,姚波1
(1.沈阳师范大学 数学与系统科学学院,辽宁 沈阳 110034;2.沈阳工程学院 基础教学部,辽宁 沈阳 110136)
摘要:针对线性系统,考虑连续增益故障模型,研究了具有执行器故障的条形区域极点配置的静态输出反馈可靠控制问题。首先,在执行器无故障的前提下,给出使极点能够配置在条形区域内的充分条件,进而得出系统的静态输出反馈可靠控制率。然后,基于执行器故障,重新设计静态输出反馈可靠控制器,利用求解线性矩阵不等式的方法,完成静态输出反馈可靠控制器的设计。由可靠控制器构成的闭环系统,使得当执行器发生故障时,也可使闭环系统的所有极点保持在条形区域内。最后,通过数值仿真验证了其结果的有效性和可行性。
关键词:极点配置;执行器故障;静态输出反馈;可靠控制;线性矩阵不等式(LMI)
反馈控制是指在控制系统中,将系统的实际输出和期望输出进行比较,形成误差,从而为确定下一步的控制行为提供依据,实现对被控对象进行控制的任务,即反馈控制原理。文献[1]提出了不确定时滞系统的反馈控制问题,并且给出了当执行器发生故障时,系统鲁棒镇定的条件。文献[2]基于线性矩阵不等式给出了保成本可靠控制器的参数化表示。文献[3]利用凸组合方法,得出当执行器发生故障时,系统渐近稳定的条件。目前反馈控制中主要是动态输出反馈和状态输出反馈,动态输出反馈结构复杂、消耗能量,状态输出反馈需要系统对状态进行采集,但一般很难做到。文献[4]给出了线性系统静态输出反馈镇定的LMI方法。文献[5]利用线性矩阵不等式方法设计了随机混合系统的无脉冲以及随机稳定的静态输出反馈控制器。文献[6]通过构造一个二次Lyapunov函数,结合线性矩阵不等式的约束条件,给出了控制器存在的充分条件。以上文献中涉及到的静态输出控制都不是可靠的,一旦系统的传感器或者执行器发生故障,系统将不再稳定,所以设计一个静态输出可靠控制是必要的,也是具有实际意义的。
可靠控制是将系统可能发生的故障考虑在系统控制器的设计过程中,主要考虑系统执行器和传感器的故障,故障类型分为“中断”故障和增益故障。自1980年Siljak发表关于可靠镇定的文章以后,许多学者对其进行了深入研究,如文献[7-9]。文献[10]给出了在连续故障的前提下,基于LMI方法的反馈控制器存在的充分条件,并且提出了考虑执行器和传感器双故障的系统完整性设计方法。文献[11]以执行器故障诊断为前提,解决了连续时间系统的可靠时滞控制问题。
区域极点配置是指把闭环系统的极点全部配置在左复平面中给出的指定区域内,那么系统将会具有所需的稳态特性和动态特性。文献[12]在考虑执行器故障的前提下,给出了扇形区域极点配置的可靠控制率。文献[13]针对不确定系统,研究了在混合故障的前提下使极点配置在圆盘区域的可靠控制问题。文献[14]研究了在一类线性系统的梯形区域极点配置问题下,执行器不同通道的增益值的容忍区间算法。
针对在条形区域下极点配置的静态输出反馈可靠控制的一些问题,通过求静态输出反馈可靠控制率的方法,论证当执行器发生故障时,使原系统极点仍旧可以配置在所确定的条形区域下的充分条件,并且利用LMI求带有执行器故障的静态输出反馈可靠控制器的设计方法,最后通过数值仿真来验证其结果的有效性和可行性。
1问题描述
考虑线性定常系统:
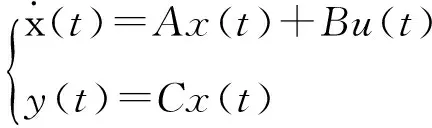
(1)
其中,x(t)∈Rn为系统的状态变量,u(t)∈Rp为系统的控制输入变量,y(t)∈Rm是系统的输出变量,A∈Rn×n和B∈Rn×p是不依赖系统的常规矩阵,C∈Rm×n是系统的测量行满秩矩阵。
执行器连续增益故障矩阵模型为
uf(t)=Fau(t)

故障处理(凸组合法):

Δa={Fa|Fa=diag(fa1,fa2,…,fap),

由文献[15]可知:
引理1:已知S是n×n正定对称矩阵(m≤n),G是适维行满秩矩阵,则矩阵GSG′可逆。
分析:证明GSG′可逆,等价于证明方程GSG′X=0只有零解。
证明:
设GSG′X=0
∵XGSG′X=0整理得(G′X)′S(G′X)=0
∵S是n×n正定对称矩阵
∴G′X=0
故有GG′X=0
又∵GG′可逆,则只有零解X=0
综上可得,方程只有零解,即GSG′可逆,引理得证。
引理4:根据引理3,矩阵A的所有特征值均在(h1,h2)的条形区域内的充分必要条件是存在对称正定矩阵X,使得
2主要结论
首先,给出了正常线性系统静态输出反馈可靠控制器设计,对线性系统(1)引入静态输出反馈控制器:
u(t)=Ky(t)
(2)
由此得到闭环系统:

(3)
定理1:对于闭环系统(3),存在静态输出反馈控制器(2),使其满足引理4的充分条件为对于正定对称矩阵X和矩阵U,使得下列线性矩阵不等式(4)存在可行解。
(4)
如果可行解为(X,U),则相应的静态输出反馈控制器为K=UW-1。其中,∏=AX+BUC,W可以由WC=CX求得。
证明:由引理4可知,把闭环系统(3)的极点配置在规定的条形区域内必须满足:
整理可得
故有
即
也就是不等式(4),其中,WC=CX,U=KW,∏=AX+BUC。
下证W可逆:
对等式WC=CX两边乘以C′得WCC′=CXC′
则W=CXC′(CC′)-1
即证CXC′可逆。
由引理1可知CXC′可逆,故W可逆。
定理得证。
然后,讨论系统发生执行器故障时,线性系统静态输出反馈可靠控制器的设计方法。
当线性系统发生执行器故障,系统可以描述为
(5)
对系统(5)引入静态输出反馈控制器:
u(t)=Ky(t)
(6)
由此得到闭环系统:
(7)
定理2:对于闭环系统(7),如果存在静态输出反馈控制器(6),使其满足引理4的充分条件为对于正定对称矩阵X和矩阵U,线性矩阵不等式(8)均存在可行解。
(8)
如果可行解为(X,U),则相应的静态输出反馈控制器矩阵增益为K=UW-1。其中,Ω=AX+BφaiUC,W可以由WC=CX求得。
证明:由引理5可知,把闭环系统(7)的极点配置在规定的条形区域内必须满足:
整理得
故有
(9)


故有
整理可得
即不等式(8)。
其中,U=KW,Ω=AX+BφaiUC,WC=CX。
3数值仿真
首先,考虑正常的线性系统在无故障的情况下,通过设计静态输出反馈控制器使闭环系统的极点在条形区域内;再考虑正常的线性系统发生执行器故障,闭环系统的部分极点无法配置在条形区域,通过重新设计控制器,使系统达到稳定。
对于相同系统考虑同一故障给出条形区域极点配置图像。系统如下:

设计静态输出反馈控制器为
使闭环系统(3)的极点在条形区域内,如图1所示。

图1 正常系统极点配置在条形区域内
考虑发生执行器故障F=diag(f1,f2),其中0≤f1≤1,0.5≤f2≤1.2,原控制器无法使所有极点均配置在条形区域,如图2所示。

图2 部分极点不在条形区域内
针对同一故障,设计新的静态输出反馈控制器为
使闭环系统极点全部配置在条形区域内,如图3所示,在F=diag(f1,f2)、0≤f1≤1、0.5≤f2≤1.2的故障前提下,重新设计静态输出反馈控制器,使所有极点均配置在条形区域内。

图3 所有极点均在条形区域内
4结论
针对线性系统研究了条形区域下具有执行器故障的区域极点配置的静态输出反馈可靠控制问题。首先在不考虑故障的情况下,通过设计控制器使所有极点可以配置在条形区域下;然后系统发生故障,在原控制器的作用下,部分极点无法配置在条形区域下;最后针对同一系统同一故障,通过设计可靠控制器,使系统的所有极点可以配置在同一条形区域下,并通过数值仿真以及系统状态响应曲线证明了可靠控制器的有效性。
参考文献
[1]徐兆棣,张嗣瀛.不确定时滞系统的输出反馈可靠控制[J].东北大学学报,2000,21(6):583-585.
[2]任俊超,胡刚,谢湘生.不确定广义系统的保成本可靠控制[J].系统工程与电子技术,2003,25(9):1122-1134.
[3]刘玉忠,王立敏,史书慧.确定切换系统的可靠控制[J].计算技术与自动化,2007,26(3):17-20.
[4]Wang Jin-zhi,Zhang Ji-feng.An LMI ApproachI to Static Output Feedback Stabilization of Linear System[J].Control Theory and Application,2001,18(6):843-846.
[5]Boukas E K.Static output feedback control for stochastic hybrid systems:LMI approach[J].Automatica,2006,42(1):183-188.
[6]Wang Jun-wei,Wu Huai-ning,Li Han-xiong.Static output feedback control design for linear MIMO systems with actuator dynamics governed by diffusion PDEs[J].International Journal of Control,2014,87(1):90-100.
[7]Veillette R J,Medanic J V,Perkins W R.Design of reliable control system[J].IEEE Transaction on Automatic Control,1992,37(3):770-784.
[8]王福忠,姚波,张嗣瀛.具有执行器故障的保成本可靠控制[J].东北大学学报,2003,24(7):616-619.
[9]Ma Li-chao,Meng Xiu-yun,Liu Zao-zhen,et al.Multi-objective and reliable control for trajectory-tracking of rendezvous via parameter-dependent Lyapunov functions[J].Acta Astronatica,2012,81(1):122-136.
[10]王福忠,姚波,张庆灵.基于LMI双故障动态输出反馈完整性控制[J].控制理论与应用,2006,23(6):976-980.
[11]乔军丽,贾新春,刘博.具有执行器故障的连续时间系统的可靠时滞控制[J].中北大学学报,2006,27(2):109-111.
[12]姚波,王福忠.部分扇形区域极点配置的可靠控制[J].计算技术与自动化,2004,23(4):5-10.
[13]王建华,姚波,黄珊.线性不确定系统混合故障的可靠圆盘极点配置[J].计算技术与自动化,2011,30(1):12-16.
[14]于洁,王福忠,姚波,等.梯形区域下执行器增益偏差容忍区间的分析[J].沈阳工程学院学报:自然科学版,2015,11(2):171-175.
[15]Ge Di,Wang Fu-zhong,Yao Bo.Static Output Feedback Reliable Control with Actuator Failures[C]//Industrial Engineering.Machine Design and Automation & Computer Science and Application.Sanya:World Scientific,2014:479-483.
(责任编辑张凯校对佟金锴魏静敏)
Static Output Feedback Reliable Control of Pole Placementin Bar Region
XU Yi-chao1,WANG Fu-zhong2,YAO Bo1
(1.College of Mathematics and System Science,Shenyang Normal University,Shenyang 110034; 2.Department of Preparatory Courses,Shenyang Institute of Engineering,Shenyang 110136,Liaoning Province)
Abstract:A static output feedback reliable control of pole placement with actor faults in bar regionofa linear systemwas proposed,considered the continuous fault mode.First,we studied the system without any faults.We got a feedback reliable controller when the poles were in the bar region,but the controller would lose efficacy when the system had actor faults.Then under the actor faults,the Lyapunoytheory was usedto deduce the sufficient condition that made all the poles werestill in the same bar region.A static output feedback reliable controller was obtained by using linear matrix inequality.A simulation example illustrates the feasibility and effectiveness of the results.
Key words:pole placement; actor faults; static output feedback; linear system; reliable control; linear matrix inequality(LMI)
中图分类号:O151
文献标识码:A
文章编号:1673-1603(2016)02-0187-06
DOI:10.13888/j.cnki.jsie(ns).2016.02.020
作者简介:徐艺超(1992-),女,辽宁沈阳人,硕士研究生。通讯作者: 王福忠(1963-),男,辽宁沈阳人,教授,博士,硕士生导师,主要从事模糊控制、动态系统的鲁棒控制和容错控制方面的研究。
收稿日期:2015-12-30

