提高定位精度及完好性增强的GBAS实验系统开发
张新辉,姜 姗,刘 军,张立立
(东北大学 信息科学与工程学院,辽宁 沈阳 110819)
提高定位精度及完好性增强的GBAS实验系统开发
张新辉,姜姗,刘军,张立立
(东北大学 信息科学与工程学院,辽宁 沈阳 110819)
摘要:针对GBAS地面系统的增强技术提出一种提高定位精度及完好性增强的改进算法。首先通过载波相位数据预处理,修正和去除周跳及残差,并引入无码载偏离平滑技术来解决电离层误差加剧问题,使平滑伪距的定位精度得到提高。在完好性方面,引入示警阈值辅助法,能够有效地避免较大偏差卫星伪距修正量的误差估计对接收机的整体剔除。在地面发射VDB报文前,验证了所发射伪距修正量的正确性。实验表明,新算法可有效减少电离层误差和较大伪距修正量误差对星基导航精密进近的精度影响。
关键词:GBAS;定位;精度;完好性
航空导航技术主要分为陆基导航和星基导航2大类。陆基导航由于台站部署难度大、电磁环境要求高、服务容量小等问题,使其发展严重受限。随着我国航空事业的快速发展,新建机场数量增多,空域结构复杂,由于地貌及建筑物的遮挡,可见卫星数量降低,星基导航的可用性和精确性难以满足应用的要求,这已成为导航技术的热点及难点问题。
为满足飞行进程阶段的各方面性能,引入了卫星导航地基增强系统(GBAS,ground-based augmentation systems)[1-2]来提高导航性能。该系统利用卫星导航差分定位技术和完好性技术来增强卫星导航系统信号,提高系统的定位精度和完好性指标,以满足飞机进场导航性能要求。
利用实时的高精度载波相位观测值对测码伪距进行相位平滑,能够有效地抑制接收机测量噪声和多路径效应的影响,大大提高测码伪距的精度[3-4]。载波相位平滑伪距通过伪距观测量和载波相位观测量的组合达到提高伪距观测量精度的目的,然而这种提高受限于多种因素,例如包括电离层延迟误差在内的相关参数的估计精度,平滑时间常数的选取等,使其单点定位精度仍难以满足高精度导航任务的需求,无法达到辅助精密进近的目的。GBAS系统中地面完好性监测[5-6]是系统实现的技术难点。LGF通常采用多台基准接收机的冗余信息进行数据的完好性监测,为交叉冗余校验构造的B值[7],校验量便是对一组基准接收机中的每个独立基准接收机伪距分修正量进行比较,完成多参考一致性监测[8]。但由于B值基于测量域构建,使其难以区别故障点分布于接收机或是卫星,剔除超过阈值接收机的单一接收机,造成可用卫星集合选择性下降。所以,针对定位精度和完好性方面存在的问题,提出了在电离层误差和精密星历改进后,又加入了示警阈值的辅助算法,并在GBAS系统中进行实际运行验证,通过与最小二乘定位算法相比,有效地提升了系统性能。
1定位精度改进算法
GBAS中北斗接收机单点定位算法直接影响到系统性能。针对加权最小二乘算法在定位中误差较大的问题,利用载波相位平滑伪距原理[9]代替纯伪距定位算法来进行单点定位,并引入无码载偏离平滑技术修正电离层误差,可有效地提高定位精度。根据载波相位平滑伪距原理,整周模糊度是不确定量,是影响载波相位平滑伪距的关键因素,所以平滑过程中的周跳和残差问题会直接影响定位的精度,需首先对周跳和残差进行修正和去除。
(1)
将载波相位观测方程和伪距观测方程进行组合,观察其特点,寻找周跳的位置。通过对历元间的差值进行检测,如果历元差是连续的,则不存在周跳;反之,则可检测出周跳及其位置。为了减少偶然性,在同一载波弧段上选取多个历元值。根据载波相位与码伪距观测量的关系:λ(CP1-CP0)≈PR1-PR0,选取相邻的历元,规定M=|λ(CP1-CP0)-(PR1-PR0)|为判决是否发生周跳的依据。这样可检测出两个载波上的周跳差n3=n1-n2。
m1-m2+ε1-ε2
(2)
由于电离层的延迟等影响在连续的历元内变化小,所以可以利用残差组合,这个组合可在周跳的位置出现明显的跳跃,在跳跃的位置前后利用多组差拟合来求出n2。
LID=αλ1N1-bλ2N2+αε1-bε2+αγ1-bγ2
(3)
经过上述步骤,将载波相位观测数据中的大部分周跳和噪声残差等进行清除,然后进一步对电离层误差进行处理,步骤如下:
1)在伪距平滑前,将伪距减去消除电离层偏差影响的相位值;
2)将得到的结果输入到滤波器进行消噪平滑;
3)在平滑后的结果中加上消除电离层偏差影响的相位值;
4)利用得到的无码载偏离影响的载波相位平滑伪距值,此伪距值计算的伪距改正数可将伪距域电离层延迟基本上完全消除干净。
2完好性增强
提高陆基增强系统的完好性是加强该系统导航能力的一个重要举措。在RTCA的LAAS(GPS的局域增强系统)规范中,定义一个参数B来判断地面广播站播送的伪距纠正量误差的正确性。文献[10]介绍了B值的含义及计算方法,并将文献中计算B值时没有考虑区分卫星故障和接收机故障的不足之处引入示警阈值辅助计算法,来监测卫星故障对B值的影响。
将包含某个卫星的伪距误差纠正量的平均值与不包含该卫星的伪距误差纠正量的平均值的差值定义为d。d的计算方法与求B值相似,只是将求B值对M个接收站伪距误差的平均值换成对N颗卫星伪距误差的平均值。卫星之间距离相隔遥远,所以不同卫星的系统误差是不同的。根据文献[11]可以求得此时的示警阈值,计算步骤如下:
1)根据所有的伪距误差纠正量求A值和阈值,并判断A值是否超过阈值;
2)若没有超过阈值,计算B值,并判断B值是否超过阈值;若超过,排除相应的误差纠正量,再计算B值,并判断B值是否超过阈值;
3)若B值没有超过阈值,则广播站播发伪距误差;若超过,排除相应的误差纠正量,再播发伪距误差。
完好性程序部分伪代码如下:
计算伪距修正量double pr,pr1,pr2;
计算B值 bias.bias=(pr+pr1+pr2)/3;
bias.b1=bias.bias-(pr1+pr2)/2;
bias.b2=bias.bias-(pr+pr2)/2;
bias.b3=bias.bias-(pr+pr1)/2;
double b1Abs=Math.Abs(bias.b1);
double b2Abs=Math.Abs(bias.b2);
double b3Abs=Math.Abs(bias.b3);if(b1Abs>=0.5 && b2Abs<0.5 && b3Abs<0.5)
{//b1不符合条件
bias.bias=(pr1+pr2)/2;}
else if(b1Abs<0.5 && b2Abs>=0.5 && b3Abs<0.5)
{//b2不符合条件
bias.bias=(pr+pr2)/2;}
else if(b1Abs<0.5 && b2Abs<0.5 && b3Abs>=0.5)
{//b3不符合条件
bias.bias=(pr+pr1)/2;}
return bias;
3仿真及性能分析
3.1GBAS系统的构建与调试
利用4台参考接收机,以传统的相位平滑伪距值作为参照值,通过数据处理中心,最终形成新的伪距差分修正值。在飞行进场阶段,进场飞机与参考接收机的距离一般不超过50 km,因此可以假设参考接收机的误差和飞机定位误差一致。
采用4台GPS/BEIDOU基准接收机搭建实验平台,放置于实验室顶楼,接收北斗导航系统信号。其中3台接收机作为基准站放置地面并进行单点定位的解算,1台接收机作为机载端定位。采用高动态测量数据,解调出载波相位值和码相位值,采样时间间隔为1 s,观测历元用时2 500 s。将3台基准站收到的卫星相关信息、伪距、实际距离等数据同时传输到中心处理站,中心处理站利用PC机对收到的参考接收机信息进行差分计算并检测其完好性。实验中数据经历载波平滑伪距、差分修正、B值计算等最终实现地面站增强功能。中心处理站将计算的差分值及B值传输给机载端,在机载端将中心处理站收到的差分值等信息与自身定位信息进行差分处理,得到定位结果,测试的运行界面如图1所示。图1中,左侧显示了机载端定位搜到的GPS、北斗信息定位坐标和伪距信息,中间部分为从中心处理站接收到的伪距修正量和计算出的B值,最右侧为利用伪距差分值和完好性信息重新计算的定位信息。

图1 机载端差分定位
3.2仿真与性能分析
对该实验系统进行24 h观测,监测实验系统精度、误差、完好性等各项指标,并进行仿真分析。
当采用基本的伪距定位算法时,定位精度随着空间星座分布的变化情况如图2所示。星座合理分布时,纯伪距定位精度在10 m左右;星座分布结构变化时,接收机的搜星个数无法满足定位算法,进而无法解算定位信息,造成个别时间定位误差很大。当采用载波相位平滑伪距差分定位算法时,定位精度可控制在3~5 m。这是因为载波相位平滑伪距差分定位算法在进行定位时,将收到的伪距差分值加入到算法中,并对伪距信息进行修正,提高了定位精度。
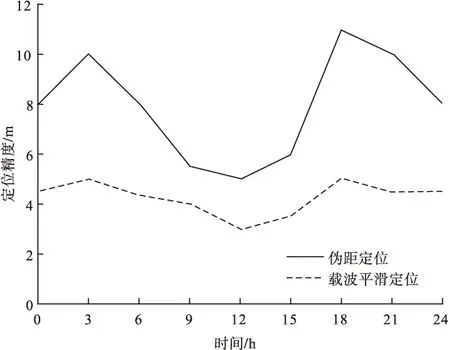
图2 定位精度分析

图3 总体误差分析
不同历元时,总体误差的变化趋势如图3所示。从图中可以看出,采用载波相位平滑伪距差分定位算法的误差明显低于纯伪距定位。这是因为算法中采用无码载偏离平滑技术,减少了电离层误差的加剧问题,使系统总体精度得到提高。
北斗24 h观测d值、示警阈值的变化趋势如图4所示。实验开始于中午卫星观测较好的情况下,人为加入误差,造成卫星不可用,此时可以看出:由于B值定义的缺陷,加入误差时,B值并无较大变化,而d值出现较大波动,超过示警阈值,进行报警,表示卫星故障,算法中去除此卫星重新进行定位。因此,该算法可以有效地进行完好性的监测。
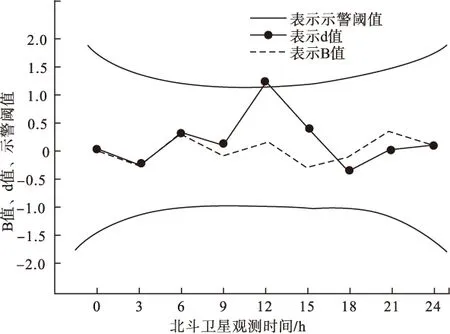
图4 完好性监测
4结语
通过对GBAS地基增强系统的实际运行和仿真分析,在载波相位平滑伪距差分定位算法中,通过对数据的预处理,去除了周跳和残差的影响,并且利用误差修正滤波使电离层误差显著降低,使定位精度有所提升。在完好性方面,该系统加强了基准接收机伪距修正量的一致性监测,新算法对于卫星故障具有更好的监测能力。该算法总体提高了地基增强辅助定位系统的差分修正量的可用性水平和完好水平性。
参考文献
[1]王雷,倪少杰,王飞雪.地基增强系统发展及应用[J].全球定位系统,2014,39(4):26-30.
[2]Murphy T,Imrich T. Implementation and Operational Use of Ground-based Augmentation Systems-A Component of Future Air Traffic Management System[J].Proceedings of the IEEE,2008,96(12):1936-1957.
[3]PRATAP MISRA,PER ENGE.Global Positioning System:Signals,Measurements,and Performance[M].Massachusetts:Ganga-Jamuna Press,2001.
[4]叶世榕.GPS非差相位精密单点定位理论与实现[D].武汉:武汉大学,2002.
[5]Dautermann T,Mayer C,Antreich F,et al.Non-Gaussian error modeling for GBAS integrity assessment.(ground based augmentation)(Technical report)[J].IEEE Transactions on Aerospace and Electronic Systems,2012,48(1):693-707.
[6]Schuster,Wolfgang,Ochieng,et al.Novel Integrity Concept for CAT III Precision Approaches and Taxiing:Extended GBAS(E-GBAS)[J].Journal of Navigation,2011,64(4):695-710.
[7]Li L,Quddus M,Ison S,et al.Multiple reference consistency check for LAAS:A novel position domain based approach[J].GPS Solutions,2012,16(2):209-220.
[8]杨文辉,周保军.LAAS地面系统多基准一致性检测算法的分析[J].电子报,2006,34(3):469-471.
[9]张成军,杨力,陈军.提高GPS载波相位平滑伪距定位精度的算法研究[J].大地测量与地球动力学,2009,29(4):106-110.
[10]Gang Xie.Integrity design and updated test results for the Stanford LAAS integrity monitor tested[C]//ION 57 th Annual Meeting/CIGTF 20th Biennial Guidance Test Symposium.Albuquerque,NM:The Institute of Navigation,America,2001:681-693.
[11]Swider R,Kaser K,Wullschleger V,et al.Technical and Programmatic Features of the FAAs LAAS[J].Journal of Navigation,1999,52(2):217-234.
(责任编辑张凯校对佟金锴魏静敏)
GBAS Experimental System Development with Enhanced Position Accuracy and Integrity
ZHANG Xin-hui,JIANG Shan,LIU Jun,ZHANG Li-li
(College of Information Science and Engineering,Northeastern University,Shenyang 110819,Liaoning Province)
Abstract:An improved algorithm to enhance the position accuracy and integrity of GBAS ground system was put forward.The ionosphere′s intensified error was reduced to solve and improve the positioning accuracy of the smooth pseudo range with the preprocessed carrier phase data by the algorithm revising and the cycle slip and residual error removed and then introducing the non code loading deviation smoothing technology.The entire elimination to the receiving machine because of the large deviation satellite pseudo range correction′s error estimation was effectively avoided by introducing the warning threshold auxiliary method.The correctness of the launched pseudo range correction was verified before the ground launched a VDB message.The experiment shows that the new algorithm can effectively reduce the influence of ionosphere and large pseudo range correction′s error on the satellite based navigation precision approach′s accuracy.
Key words:GBAS; Positioning; Accuracy; Integrity
中图分类号:V556
文献标识码:A
文章编号:1673-1603(2016)02-0163-05
DOI:10.13888/j.cnki.jsie(ns).2016.02.015
通讯作者:刘军(1969-),男,辽宁沈阳人,副教授,博士,主要从事星基导航及增强系统、空间信息网络、移动自组织网络等方面的研究。
作者简介:张新辉(1994-),男,河北张家口人。
基金项目:国家自然科学基金(61401079,61151002,61151002),中国航天科技集团公司卫星应用研究院创新基金(2014-CXJJ-TX-11)
收稿日期:2015-11-30

