基于人均GDP差异的生活用水量模拟及增长潜力分析

马黎华，粟晓玲

(1 西南大学 资源环境学院，重庆 北碚 400715； 2 西北农林科技大学 水利与建筑工程学院，陕西 杨凌 712100)



基于人均GDP差异的生活用水量模拟及增长潜力分析

马黎华1，粟晓玲2

(1 西南大学 资源环境学院，重庆 北碚 400715； 2 西北农林科技大学 水利与建筑工程学院，陕西 杨凌 712100)

[摘要]【目的】 分析城市居民人均生活用水量的增长潜力，为保障城市用水安全提供决策依据。【方法】 以2009-2011年858个中国城市用水及相关数据为研究对象,应用线性回归模型、幂函数模型、对数函数模型和ANN-BP模型，基于人均GDP的差异分别建立人均生活用水量模型,进行人均生活用水量的增长潜力分析。【结果】 在不同的人均GDP水平下，模型对于高收入的数据样本最为敏感；线性回归模型、幂函数模型和ANN-BP模型的模拟效果较为接近，对数函数模型的误差最大。人均生活用水量增长潜力最大的是年人均GDP低于3万元的城市，增长潜力最小的为年人均GDP >3～≤10万元的城市。【结论】 基于人均GDP差异可以进行生活用水量的模拟与预测，人均GDP小于3万元的城市将成为人均生活用水量增加的主要来源。

[关键词]城市用水；用水量预测；用水量增长潜力分析；GDP；ANN-BP模型

随着我国社会经济的迅猛发展，城市需水量增长迅速。城市用水量的增加有很大一部分来自于城市居民生活用水量的增加，居民生活用水量占总供水量的比例由2002年的19.51%上升至2012年的34.4%，因此对居民生活用水量进行模拟与合理预测有积极的现实意义。

对用水量的预测可以由其影响因素进行推求，也可以根据用水量的历史数据通过时间序列分析实现预测，例如修正组合模型[1]、小波分析[2]等。针对居民生活用水量影响因素的分析表明：城市人口的增加是城市生活用水总量增加的主要原因[3]，居民的人均生活用水量与区域经济增长密切相关[4]。同时，不同区域之间的居民用水习惯和气候特征也决定了居民生活用水量的差距，水价、平均工资、人均住房面积以及气候差异也会对居民生活用水量产生不同程度的影响[5-6]。在宏观水资源分析或者对预测精度要求不高时，可由人口与居民人均生活用水定额直接计算求得[7]。目前,根据研究的不同侧重相继提出用线性回归模型[8]、非线性回归模型[9]、计量经济学模型[10]、模糊模型[11]以及神经网络模型[12]等预测用水量，近年来基尼系数[13]和恩格尔系数[14]等也被用于用水量的预测，旨在体现居民生活水平对用水变化的影响程度。以往的研究表明，人均生活用水量往往随着经济水平的发展而变化，但是将GDP指标作为参数进行居民人均生活用水量与人均GDP的关系模拟分析比较少。基于我国GDP高速发展的现状[15]，人均GDP的巨大差异必然导致人均生活用水量的巨大差异，进行城市居民人均生活用水量随人均GDP的变化模拟,可以深入理解城市经济水平与人均生活用水量之间的响应关系，实现对未来用水增长潜力的合理预测。

本研究针对近几年中国城市居民人均生活用水量与人均GDP的关系进行模拟与分析，并对未来中国城市居民用水量的增长潜力进行了探讨，旨在对高速经济增长条件下的城市居民人均生活用水量模型进行比较与选择，有效估计GDP显著差异条件下我国城市居民人均生活用水量的未来增长潜力。

1研究方法

1.1样本数据整理

所采用的样本数据主要来自《中国城市统计年鉴》(2009-2011年)。主要指标包括：市辖区居民生活用水量(万t)、地区生产总值(万元)、年末总人口(万人)。其中2009年共选取287个地区和城市，2010年共选取285个地区和城市，2011年共选取286个地区和城市，共计858个城市的数据样本。在数据的初步处理中，已经剔除了数据不匹配的样本(如只有人口而无国内生产总值数据等)。

1.2人均GDP对生活用水量的影响程度分析

从城市之间人均GDP水平的差异入手，采用相关分析与互信息分析，研究不同收入层次下的人均生活用水量与人均GDP之间的关系。针对本研究中选用的2009-2011年的858个数据样本，为突出不同人均GDP水平的差异，按照>10万元、>5～≤10万元、>3～≤5万元、>1～≤3万元、≤1万元分为5组。

相关系数r的计算公式为：

我左冲右突，从密密的树丛中挤过去摘了两丫桃花，脸上居然划了一道血口子，不留神让一株狗儿刺拉了一下。学着绅士的模样，我毕恭毕敬地献给女友，一脸虔诚，“嫁给我吧，亲爱的。”

(1)

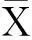
互信息(Mutual Information)的计算原理为：

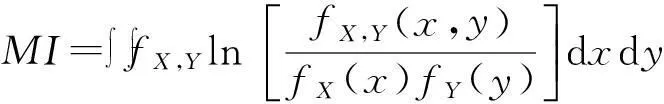
(2)

式中：MI为互信息值，fX,Y(x,y)为X、Y的联合边际分布函数，fX(x)、fX(y)为变量X、Y的边际分布函数。如果X、Y之间没有关系，MI的值为0；反之，如果随机变量X、Y关系紧密，则MI的值会很大。

1.3模型模拟与敏感性分析

采用不同的训练样本和检测样本进行模型模拟与敏感性分析，目的是比较不同类型模型的拟合优度以及对GDP水平差异的敏感程度。以2/3的样本共572组数据为建模样本，以1/3的样本共286组数据为检测样本。在模型模拟对比分析中，分别以2010与2011年为建模样本，2009年为检测样本；2009与2011年为建模样本，2010年为检验样本；2009与2010年为建模样本，2011年为检测样本。在模型敏感性分析中，将所有样本数据按照人均GDP值的大小排序，并按照每组样本数量一致的原则，将所有样本分为低收入、中收入和高收入3组，分别以低收入、中收入为建模样本，高收入为检测样本；中收入、高收入为建模样本，低收入为检测样本；高收入、低收入为建模样本，中收入为检测样本。

在模型模拟效果的评价中采用检测样本的误差比较，误差由预测值与真实值的相关系数R和均方根误差RMSE(Root Mean Square Error)表达，若R值越接近1则模型的模拟效果越好；RMSE的值越小表明模型模拟的效果越好。但由于RMSE与真实值的量纲相同，在模型预测研究中的应用更为广泛。

R的计算公式为：

(3)

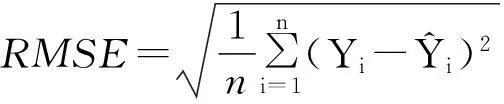
(4)

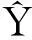
1.4人均生活用水量增长潜力分析

增长潜力分析的数据样本参照人均GDP水平在>10万元、>5～≤10万元、>3～≤5万元、>1～≤3万元、≤1万元的分组情况。基于人均GDP差异的人均生活用水量模型拟采用一元线性回归模型(以下简称为线性回归模型)、幂函数模型、对数函数模型和神经网络模型误差逆传播算法ANN-BP(ArtificialNeuralNetworks-BackPropagation)模型，运用模型求导和MC(MonteCarlo)设计分析GDP不同差异水平下未来我国城市居民人均生活用水量的增长潜力。其中线性回归模型、幂函数模型和对数函数模型的增长潜力计算由已建立的模型公式求导得到。由于ANN-BP模型为数据驱动模型，因此采用MC设计来进行增长潜力分析。按照设定的GDP年增长水平，随机生成新的输入项数据，将新的数据导入已建立的模拟模型中，然后计算模型输出结果的平均增长率，即增长潜力。

2结果与分析

2.1人均GDP对生活用水量的影响程度

将858个数据样本分成5组，这5组数据样本人均GDP范围对应的样本容量以及在这种分组情况下人均GDP与人均生活用水量的相关系数(r)和互信息值(MI)如表1所示。

表 1　人均GDP与人均生活用水量的相关分析与MI分析

注：**表示极显著相关水平，*表示显著相关水平。

Note：** stands for very significant level，* stands for significant level.

由表1可知，根据相关系数r和互信息值MI得到人均GDP与人均生活用水量关系的紧密程度略有差异。经过显著性分析发现，人均GDP与城市居民人均生活用水量的r值在人均GDP为10万元以上和3万元以下时呈显著线性相关。而基于互信息值的分析结果表明：不同的人均GDP水平与人均生活用水量的关系差异不大，>5～≤10万元时的MI值最大，人均GDP≤1万元时MI值最低。

2.2不同模型的模拟效果与敏感性分析

对不同类型模型的模拟效果与敏感性进行分析，得到不同建模数据下线性回归模型、幂函数模型、对数模型和ANN-BP模型检测样本的R值和RMSE值如表2所示。从表2中不同模型的模拟效果来看，对数函数模型的平均RMSE最大，R值最小；线性回归模型的平均RMSE最小，幂函数模型的R值最大；同时，线性回归模型、ANN-BP模型与幂函数模型的模拟效果较为接近。模型类型不同而模拟结果类似，表明人均GDP与人均生活用水量之间有较稳定的数量关系。在增长潜力分析中，可以采用线性回归模型、ANN-BP模型与幂函数模型对人均生活用水量增长潜力进行分析。

根据敏感性分析结果，在不同人均GDP水平下，以低收入和高收入为建模样本、中等收入为检测样本时，所得到的模型误差最小；以低收入和中收入为建模样本，高收入为检测样本时，所得到的模型误差最大。因此认为在不同的人均GDP水平下，模型对于高收入的数据样本最为敏感。

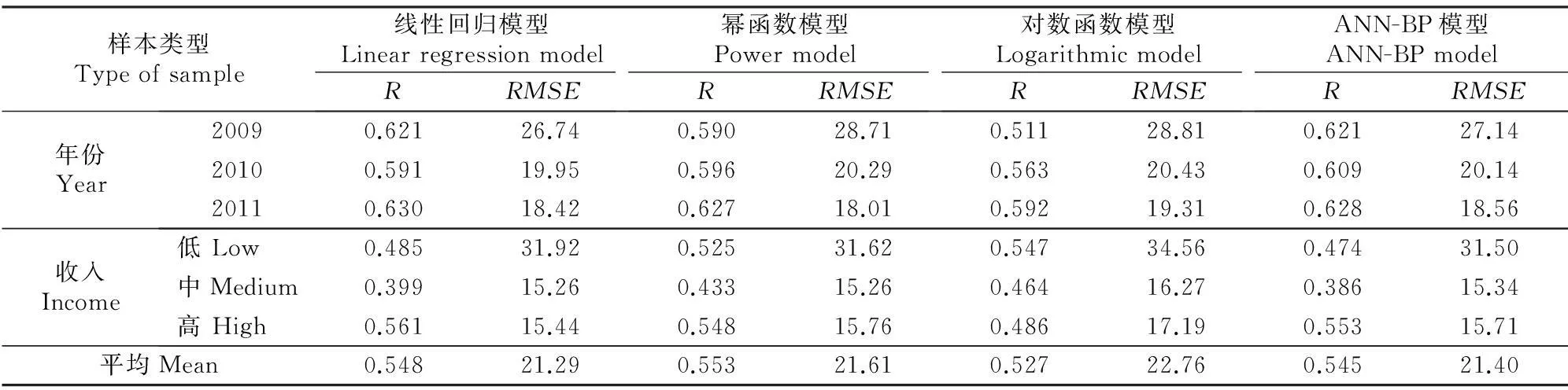
表 2　不同建模数据下多元线性回归模型、幂函数模型、对数函数模型和ANN-BP模型拟合的R与RMSE值

2.3人均生活用水量的增长潜力

2.3.1参数拟合与误差分析在不同人均GDP水平下，采用线性回归模型、幂函数模型和ANN-BP模型进行模拟分析，其中模型拟合的统计结果和误差如表3、表4所示。

表 3　不同人均GDP水平下线性回归模型与幂函数模型的拟合结果

表 4　不同人均GDP水平下线性回归模型、幂函数模型与ANN-BP模型的RMSE值

从模型整体拟合的F检验显著性来看，人均GDP水平在>10万元、>1～≤3万元、≤1万元时均可以达到α=0.05的显著性水平，其中在人均GDP为>1～≤3万元水平下模型的模拟效果最好。在人均GDP水平>5～≤10万元和>3～≤5万元时，模型未通过F检验；这与影响程度分析中相关系数r值的结果相一致(表1)。对原始数据进行再分析后发现，数据样本人均GDP水平在>5～≤10万元和>3～≤5万元时，即人均GDP的差异较大时对应的人均用水量差异却不大，二者一致性变化规律不明显是导致线性回归模型无法通过F检验的主要原因。

表4结果表明，在人均GDP>5～≤10万元和>3～≤5万元水平下各模型的拟合误差(RMSE)与其他人均GDP水平下的模型相比并不是最大，因此认为在人均GDP>5～≤10万元和>3～≤5万元水平下采用拟合系数进行的增长潜力分析仍具有一定意义。根据不同人均GDP水平下线性回归模型、幂函数模型和ANN-BP模型的RMSE值结果，可以认为幂函数模型的误差最大，线性回归模型的误差最小。

2.3.2增长潜力分析根据城市居民人均生活用水量增长潜力计算结果，人均GDP的年平均增长率设为8%，对已建立的线性回归模型、幂函数模型和ANN-BP模型进行增长潜力分析，得到基于上述模型的不同人均GDP水平下人均用水量增长率的变化情况如图1所示。

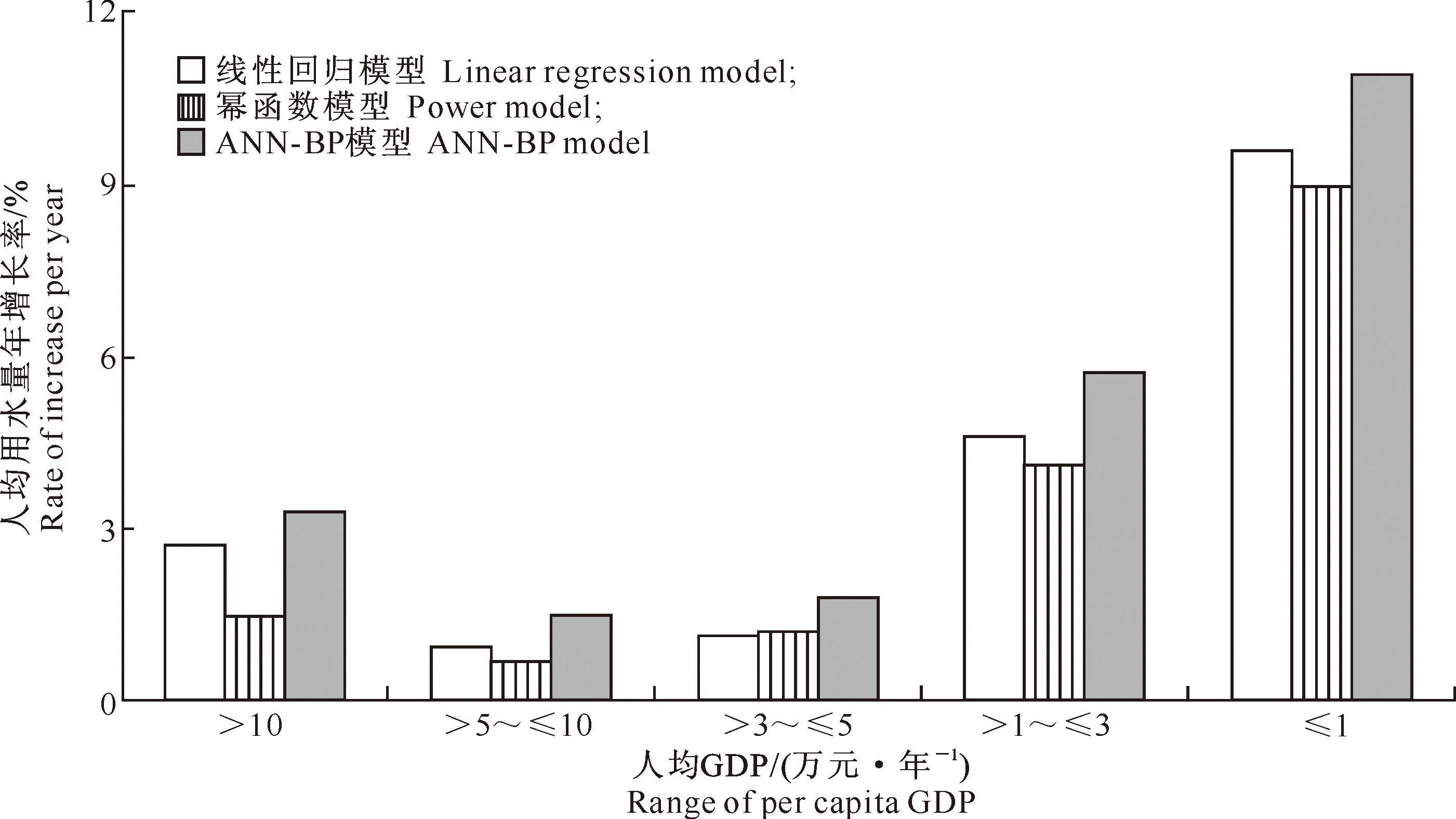
图 1　基于线性回归模型、幂函数模型和ANN-BP模型的不同人均GDP水平下用水量增长率的变化

从3种模型对人均生活用水量增长率的计算结果(图1)可以看出，人均生活用水量年增长率最大的为人均GDP≤1万元的城市，其均值为10.07%；其次是人均GDP为>1～≤3万元的城市，其均值为4.81%；人均GDP为>5～≤10万元、>3～≤5万元的城市人均生活用水量增长率最低；人均GDP>10万元城市的人均生活用水量增长率较人均GDP>5～≤10万元、>3～≤5万元的略高，为2.51%。说明我国城市人均生活用水量增长潜力最大的是低收入城市，即年人均GDP≤3万元的城市，其样本总数为355个，占全国城市样本总数的41.38%，年均用水增长潜力在年均10%左右。

3结论

本研究分别用线性回归模型、幂函数模型、对数函数模型和ANN-BP模型构建城市居民人均生活用水量与人均GDP的关系模型，并对不同人均GDP水平下的人均生活用水量增长潜力进行了进一步分析。结果表明：对数函数模型的误差最大，线性回归模型的误差最小；同时，线性回归模型、ANN-BP模型与幂函数模型的模拟效果较为接近，基于人均GDP差异可以进行生活用水量的模拟与预测。在不同的人均GDP水平下，模型对于高收入的数据样本最为敏感。我国城市人均生活用水量未来增长潜力最大的是年人均GDP低于3万元的低收入城市，较为稳定的是年人均GDP为3万～10万元的中等收入城市，位于二者之间的是年人均GDP大于10万元的高收入城市，占到我国城市比例40%左右的人均GDP小于3万元的城市会成为人均生活用水量增加的主要来源。

[参考文献]

[1]冯天梅,张鑫.基于修正组合模型的包头市用水量预测分析 [J].西北农林科技大学学报(自然科学版),2014,42(3):227-234.

Feng T M,Zhang X.Prediction of water consumption in Baotou based on amended combination model [J].Journal of Northwest A&F University(Nat Sci Ed),2014,42(3):227-234.(in Chinese)

[2]魏津瑜,苏思沁,施鹤南.基于小波分析的城市需水量预测 [J].中南大学学报(自然科学版),2013,44(S2):183-187.

Wei J Y,Su S Q,Shi H N.Urban water demand forecast based on wavelet analysis [J].Journal of Central South University(Science and Technology),2013,44(S2):183-187.(in Chinese)

[3]Alcamo J,Döll P,Henrichs T.Development and testing of the Water GAP 2 global model of water use and availability [J].Hydrological Sciences Journal,2003,48(3):317-337.

[4]Oki T,Kanae S.Global hydrological cycles and world water resources [J].Science,2006,313:1068-1072.

[5]张华丽,董婕,延军平,等.西安市城市生活用水对气候变化响应分析 [J].资源学报,2009,31(6):1040-1045.

Zhang H L,Dong J,Yan J P,et al.Urban domestic water consumption’s response to climate change in Xi’an [J].Resources Science,2009,31(6):1040-1045.(in Chinese)

[6]周景博.中国城市居民生活用水影响因素分析 [J].统计观察,2005(6):75-76.

Zhou J B.Analysis of factors affecting the Chinese city residents water use [J].Statistical Observation,2005(6):75-76.(in Chinese)

[7]王彬,穆瑞林,卜喆芬.城市生活用水预测方法的探讨 [J].中国给水排水,1990(6):32-37.

Wang B,Mu R L,Bu Z F.The method of city living water prediction [J].Chinese Water Supply and Drainage,1990(6):32-37.(in Chinese)

[8]Döll P,Hauschild M.Model-based scenarios of water use in two semi-arid Brazilian states [J].Regional Environmental Change,2002,4(2):150-162.

[9]Zhou S L,McMahon T A,Walton A,et al.Forecasting operational demand for an urban water supply zone [J].Journal of Hydrology,2002,259(3):189-202.

[10]沈大军,陈雯,罗健萍.城镇居民生活用水的计量经济学分析与应用实例 [J].水利学报,2006,37(5):593-597.

Shen D J,Chen W,Luo J P.Econometric analysis and application examples of urban household water [J].Journal of Hydraulic Engineering,2006,37(5):593-597.(in Chinese)

[11]Gato S,Jayasuriya N,Roberts P.Temperature and rainfall th-resholds for base use urban water demand modeling [J].Journal of Hydrology,2007,337(3/4):364-376.

[12]Adamowski J,Karapataki C.Comparison of multivariate regression and artificial neural networks for peak urban water-demand forecasting:evaluation of different ANN learning algorithms [J].Journal of Hydrologic Engineering,2010,15(10):729-743.

[13]李建芳,粟晓玲,王素芬.基于基尼系数的内陆河流域用水公平性评价:以石羊河流域为例 [J].西北农林科技大学学报(自然科学版),2010,38(8):217-221.

Li J F,Su X L,Wang S F.Evaluating the fairness of water use based on the Gini coefficient in inland river basins:a case study on Shiyang River basin [J].Journal of Northwest A&F University(Nat Sci Ed),2010,38(8):217-221.(in Chinese)

[14]张志果,邵益生,徐宗学.基于恩格尔系数与霍夫曼系数的城市需水量预测 [J].水利学报,2010,41(11):1304-1309.

Zhang Z G,Shao Y S,Xu Z X.Prediction of urban water demand based on Engel Index and Hoffmann Coefficient [J].Journal of Hydraulic Engineering,2010,41(11):1304-1309.(in Chinese)

[15]杨充霖,文先明.从传统GDP到可持续发展GDP的历史性转变:可持续发展GDP研究及对中国的意义 [J].北京师范大学学报(社会科学版),2008(1):134-139.

Yang C L,Wen X M.Historical change from traditional GDP to sustainable development GDP:significance of sustainable development GDP research to China [J].Journal of Beijing Normal University(Social Science),2008(1):134-139.(in Chinese)

Simulation and growth potential of domestic water consumption based on difference in per capita GDP

MA Li-hua1,SU Xiao-ling2

(1CollegeofResourcesandEnvironments,SouthwestUniversity,Beibei,Chongqing400715,China;2CollegeofWaterResourcesandArchitecturalEngineering,NorthwestA&FUniversity,Yangling,Shaanxi712100,China)

Abstract:【Objective】 This study analyzed the growth potential of urban residential water use per capita to provide basis for protection of urban water security. 【Method】 Water consumption and relevant data in 2009 to 2011 of 858 cities were analyzed using linear regression model,power model,logarithmic model,and ANN-BP model.Then,the domestic water consumption model was established based on difference in per capita GDP and it was used to analyze the growth of per capita water use.【Result】 The performance of models was most sensitive to high income data group.The error of logarithmic model was the largest while that of linear regression model,power model and ANN-BP model were similar.The cities with per capita GDP of less than 3×104 Yuan had the greatest potential for growth of per capita water use while the cities with per capita GDP of 3×104-10×104 Yuan had the smallest potential.【Conclusion】 Based on the analysis of difference in per capita GDP,the cities with per capita GDP of less than 3×104 Yuan will become the main contributor to the increase of urban residential water use per capita.

Key words:urban water use;water consumption forecasting;growth potential analysis of water consumpeion;GDP;ANN-BP model

DOI：网络出版时间:2016-04-0709:0010.13207/j.cnki.jnwafu.2016.05.018

[收稿日期]2014-09-19

[基金项目]国家自然科学基金项目(51279166；51509214)；西南大学基本科研业务费专项(XDJK2013C153)；西南大学博士基金项目(2120132467)

[作者简介]马黎华(1983-)，女，河南平顶山人，讲师，博士，主要从事水文及水资源相关数据建模研究。

[通信作者]粟晓玲(1968-)，女，四川开江人，教授，博士，博士生导师，主要从事水资源配置及生态需水研究。

[中图分类号]TV212.1

[文献标志码]A

[文章编号]1671-9387(2016)05-0133-06

网络出版地址:http://www.cnki.net/kcms/detail/61.1390.S.20160407.0900.036.html

E-mail：malihua1210@yeah.net

E-mail：suxiaoling17@126.com