基于TDDFT理论的Si8团簇结构及其电子性质的数值分析研究

胡芸莎　刘朝霞　熊 英

(1 塔里木大学机械电气化工程学院，新疆 阿拉尔 843300)(2 现代农业工程重点实验室，新疆 阿拉尔 843300)



基于TDDFT理论的Si8团簇结构及其电子性质的数值分析研究

胡芸莎1刘朝霞1熊 英2*

(1 塔里木大学机械电气化工程学院，新疆 阿拉尔 843300)(2 现代农业工程重点实验室，新疆 阿拉尔 843300)

摘要采用基于广义梯度近似(GGA)的含时密度泛函TDDFT方法对Si8团簇的空间构型与对称性，能隙及电子性质进行了模拟分析，在模拟过程中采用GGA近似方法对Si8团簇的基态能量进行截断处理。结果表明，具有C1和C2v对称性的Si8团簇的化学稳定性相对较好，具有Cs对称性的Si8团簇化学稳定性最差；具有D4d对称性构型和C2v对称性3a构型的Si8团簇的平均结合能最小，团簇的稳定性最差。

关键词Si8团簇； TDDFT理论； GGA近似

1引言

近年来，随着微纳米技术的发展，低维度纳米材料越来越成为研究者们关注的重点，低维度纳米材料的一些特性是未来制造特种光电器件的基础。团簇材料作为微观原子、分子和宏观凝聚态物质的过度介质，其性质随团簇内原子或分子的个数不同而显著差异，因此可以利用这一特性来制作某些特定功能的微观器件。

Si基材料是整个半导体工业的基础材料，有着不可替代的重要性，因而Si基团簇的性质也引人关注[1-5]。学者们基于各种精确程度的理论方法来研究Si团簇的结构和电子性质，其中最为可靠的方法仍然是基于量子力学的第一性原理计算方法，即密度泛函方法(DFT)以及含时密度泛函方法(TDDFT)等[6,7]。

团簇性质不仅随团簇内原子数量的不同而有明显地变化，它也和团簇内原子或分子的空间构型有关[8]，例如对于某一定数量的原子构成的团簇(例如Si8)，其稳定结构就具有至少5种类型的对称性和16种具体的空间构型。目前还没有对于Si8团簇对称性和构型与其性质之间的关系的研究。本文基于TDDFT理论，着重探讨Si8团簇的对称性和空间构型与其电子性质之间的关系。

2计算方法

含时密度泛函理论(TDDFT)目前是研究多粒子系统电子结构的重要方法[9,10]，应用非常广泛，它起源于Thomas-Fermi(TF)模型[11]，在Hohenberg-Kohn定理提出之后得到坚实的理论支持。密度泛函理论最普遍的应用都是通过Kohn-Sham方法实现的[12]，在Kohn-Sham(K-S)框架内多粒子系统的K-S 方程一般写为

(1)

其中vxc(r)、vH(r)和vxc(r)分别是外势、Hartree势和交换关联势。

在Kohn-Sham的框架内，电子的相互作用被简化成一个有效势场中的问题。这个有效势场包括了外部势场以及电子间库仑相互作用的影响，即交换和相关作用。处理交换相关作用是TDDFT理论的难点，最简单的近似求解方法为局域密度近似(LDA近似)[13]，除此而外常见的还有广义梯度近似(General gradient approximation，GGA)泛函理论、和杂化密度泛函(Hybrid Density Functional)理论等。

一般情况在系统的原子结合能不是很高的情况下，LDA 近似可以得出很好的结果，但是当系统内原子结合能较高时，LDA给出的结果就不太理想。为了弥补这种缺陷，在 LDA 近似基础上学者们发展了广义梯度近似泛函理论 (GGA)[14]，在GGA理论中，系统的交换相关势写为

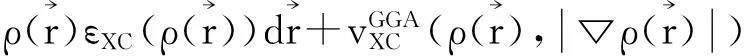
(2)

一般常用的GGA近似方法有两种：Perdew-Wang (PW91)[15]和 Perdew-Burke-Ernzerhof (PBE)[16]。

本文的计算是通过基于含时密度泛函理论(TDDFT)的计算软件Materials Studio (MS)所集成的Dmol3软件包完成的，采用含时密度泛函理论(TDDFT)下的广义梯度近似(GGA)在计算中采用了半局部 PW91交换关联泛函，采用 Gaussian smearing 方法，展宽为 0.005eV。

所有的计算均是在Fine网格下完成的，采用带极化的双数值原子基组(DNP)进行全电子计算，自洽过程以体系的能量和电荷密度分布是否收敛为依据，精度均优于10-5a.u.，梯度和位移的收敛精度优于2.0×10-3a.u./nm和5.0×10-3nm，能量的收敛精度优于1.0×10-5a.u.。

3结果与分析

3.1团簇结构及对称性分析

最低能量结构的Si8团簇的对称性主要有C1，C2，C2v，Cs和D4d等几种，如图1所示，在每一种对称性下，又有几种不同的空间构型。每一种构型对应的能量参数各不相同。C1对称性有4种构型(图1a-图1d)，其中图1a和图1b构型的最小振动频率在100 Hz以上，图1c和图1d构型的最小振动频率在50 Hz-60 Hz范围内；具有C2对称性的Si8团簇的稳定构型有3种，如图2a，2b和2c中所示，不同构型之间最小振动频率差别很大；具有C2v对称性的Si8团簇的稳定构型也有3种，分别是构型3a，3b和3c，同样可以看到构型3a，3b和3c之间的最小振动频率差别很大；具有Cs对称性的Si8团簇的稳定构型有5种，分别是构型5a，5b，5c，5d和5e，具有Cs对称性的稳定构型的最小振动频率相较于其它对称性的构型来说整体偏小；具有D4d对称性的Si8团簇的稳定构型只有1种，如图5a中所示，这种构型的Si8团簇具有类似石墨烯的层状结构。

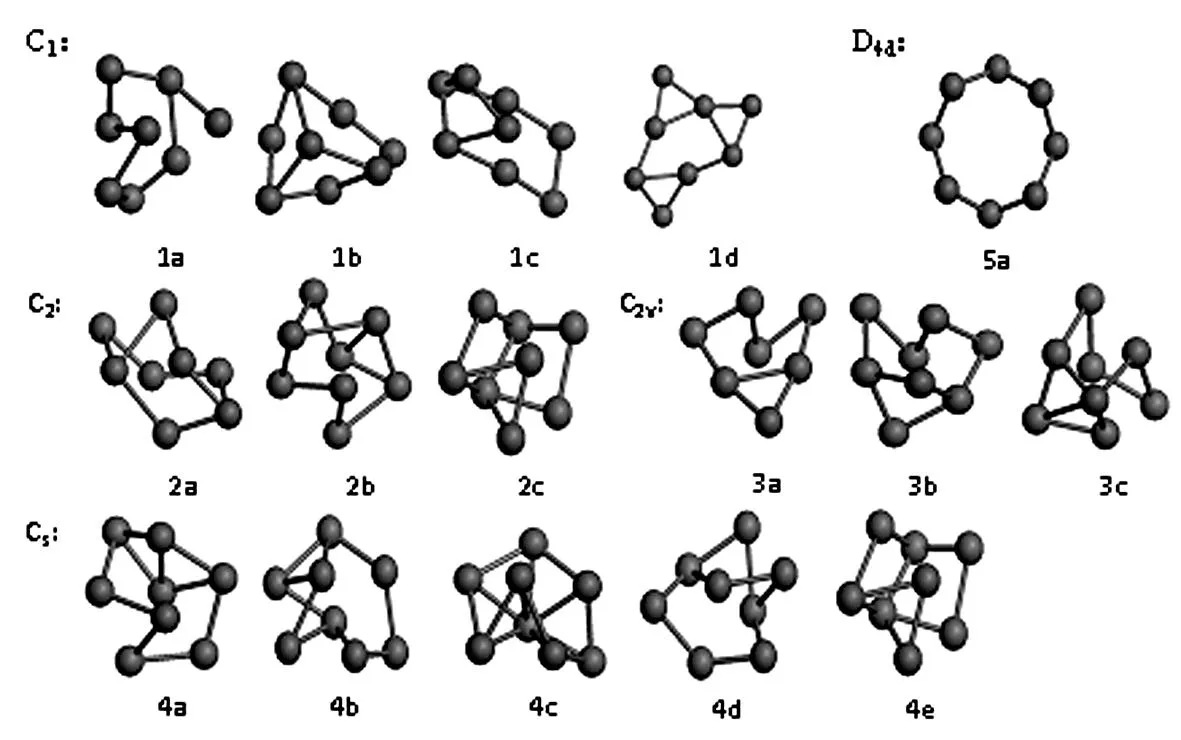
图1　在不同对称性下最低能量结构的Si8团簇的空间几何构型

3.2Si8团簇的电子性质分析

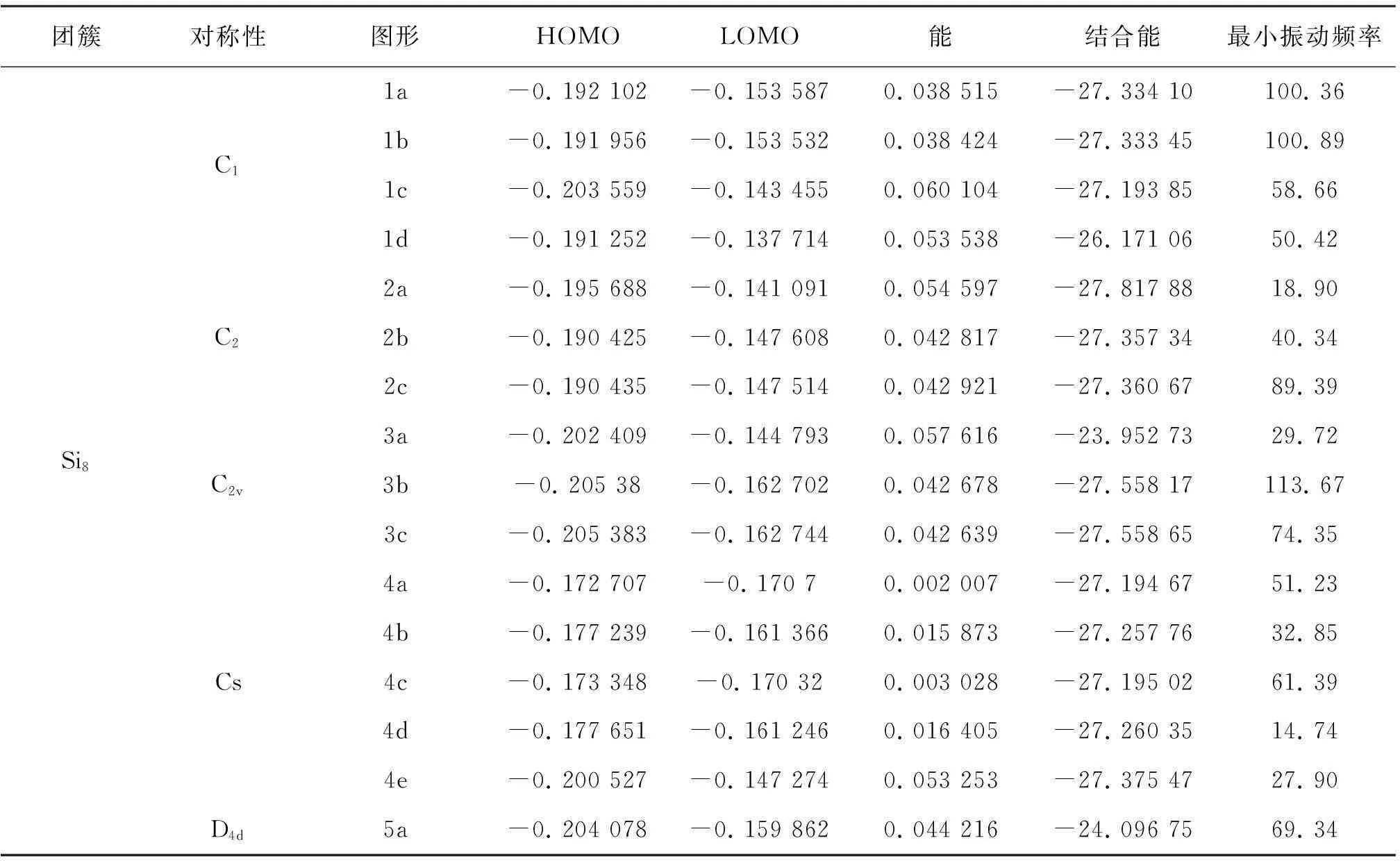
表1　最低能量结构的Si8团簇的结构和电子性质参数

平均结合能是表征原子或分子稳定性的重要参数，结合能数值越大，分子或原子的就越稳定。对于Si8团簇，表1 给出了其不同对称性下的最低能量结构的平均结合能Eb。从表1中不难发现具有D4d对称性构型和C2v对称性3a构型的Si8团簇的平均结合能最小，其它对称性和构型的Si8团簇的平均结合能相差不大。这是因为在D4d对称性以及C2v对称性3a构型下，Si8团簇的Si原子的悬挂键最多，导致其结合能偏小，稳定性最差。

表2　具有不同对称性的Si8团簇的平均能隙

能隙反映了电子从占据轨道向未占据轨道发生跃迁的能力，在一定程度上反映了团簇参与化学反应的能力。为了更进一步研究团簇的相对稳定性，表2给出了不同对称性下最高已占据轨道(HOMO)与最低未占据轨道(LUMO)之间的平均能隙Egap。 从表中可以看出，具有C1对称性的Si8团簇的平均能隙最高，具有Cs对称性的Si8团簇的平均能隙最低，说明具有C1和C2v对称性的Si8团簇的化学稳定性相对较好，具有Cs对称性的Si8团簇化学稳定性最差，最容易失去电子从而参加化学反应。

4结论

采用含TDDFT理论的广义梯度近似(GGA)对Si8团簇的几何结构进行了优化，并对其对称性，空间构型以及电子性质进行了模拟分析。计算中发现，具有D4d对称性构型和C2v对称性3a构型的Si8团簇的平均结合能最小，团簇的几何结构稳定性最差，最易发生变形。对于Si8团簇，其C1和C2v对称性的空间几何结构的化学稳定性相对较好，而Cs对称性的空间几何结构化学稳定性最差。

参考文献

[1]Kaxiras E. Structural model for a covalently bonded Si45cluster[J]. Chemical physics letters, 1989, 163(4): 323-327.

[2]Kanzawa Y, Hayashi S, Yamamoto K. Raman spectroscopy of Si-rich films: possibility of Si cluster formation[J]. Journal of Physics: Condensed Matter, 1996, 8(26): 4823.

[3]Sun Q, Wang Q, Jena P, et al. First-principles studies of the geometry and energetics of the Si36cluster[J]. Physical Review A, 2003, 67(6): 063201.

[4]Watanabe M O, Uchida N, Kanayama T. Impact-energy dependence of hydrogenated Si cluster deposition on Si (111)(7× 7)[J]. Physical Review B, 2000, 61(11): 7219.

[5]Kanemitsu Y, Suzuki K, Kondo M, et al. Luminescence from a cubic silicon cluster[J]. Solid state communications, 1994, 89(7): 619-621.

[6]Gidopoulos N I, Wilson S. The fundamentals of electron density, density matrix and density functional theory in atoms, molecules and the solid state[M]. Springer Science & Business Media, 2003:.

[7]Density functional theory[M]. Springer Science & Business Media, 2013: .

[8]柳福提, 程艳, 羊富彬, 等. Si4团簇电子输运性质的第一性原理计算[J]. 物理学报, 2013, 62(14): 140504-140504.

[9]Marques M A L, Gross E K U. Time-dependent density functional theory[J]. Annual Review of Physical Chemistry, 2004, 55(1): 427-455.

[10]Gross E K U, Kohn W. Time-dependent density functional theory[J]. Adv. Quant. Chem, 1990, 21: 255-291.

[11]Schwinger J. Thomas-Fermi model: The second correction[J]. Physical Review A, 1981, 24(5): 2353.

[12]Tsuneda T. Kohn-Sham Method[M]. Density Functional Theory in Quantum Chemistry. Springer Japan, 2014: 79-99.

[13]Yabana K, Bertsch G F. Time-dependent local-density approximation in real time[J]. Physical Review B, 1996, 54(7): 4484.

[14]Perdew J P, Burke K, Ernzerhof M. Generalized gradient approximation made simple[J]. Physical review letters, 1996, 77(18): 3865.

[15]Burke K, Perdew J P, Wang Y. Derivation of a generalized gradient approximation: The PW91 density functional[M]. Electronic Density Functional Theory. Springer US, 1998: 81-111.

[16]Adamo C, Barone V. Physically motivated density functionals with improved performances: The modified Perdew-Burke-Ernzerhof model[J]. The Journal of chemical physics, 2002, 116(14): 5933-5940.

The Numerical Analysis of the Structural Symmetry and Electronic Properties of Si8Clusters Based on the TDDFT Theory

Hu Yunsha1Liu Zhaoxia1Xiong Ying2*

(1 College of mechanical and electronic engineering，Tarim university，Alar，Xinjiang 843300)(2 Key Laboratory of modern agricultural engineering，Tarim university，Alar，Xinjiang 843300)

AbstractThe space configuration and symmetry，energy gaps and electronic properties of Si8 clusters have been simulated by using TDDFT theory which based on the Generalized Gradient Approximation (GGA) method. The results show that the chemical stability of Si8 clusters with C1 and C2vsymmetry be relatively good than that with Cs symmetry, and the average binding energy of the Si8 clusters with D4dsymmetry and 3A configuration under C2vsymmetry will be minimum.

Key wordsSi8 clusters； TDDFT theory； GGA approximation

中图分类号：G237．5

文献标识码：A

DOI：10.3969/j.issn.1009-0568.2016.02.016

文章编号：①1009-0568(2016)02-0093-05

作者简介：胡芸莎(1983-)，女，实验师，研究方向为凝聚态物理。E-mail：79292006@qq.com*为通讯作者E-mail：65587588@qq.com

基金项目：塔里木大学校长基金青年项目(TDZKQNZK201401)。

收稿日期：①2015-10-05