基于生态位理论的多模型秦岭山区建设用地适宜性评价——以商洛市商州区为例

张 海 龙,郭 彦 龙,高 蓓

(1.商洛学院城乡规划与建筑工程学院，陕西 商洛 726000；2.中国科学院寒区旱区环境与工程研究所,甘肃 兰州 730000；3.陕西省农业遥感信息中心，陕西 西安 710015)

基于生态位理论的多模型秦岭山区建设用地适宜性评价
——以商洛市商州区为例

张 海 龙1,郭 彦 龙2,高 蓓3

(1.商洛学院城乡规划与建筑工程学院，陕西 商洛 726000；2.中国科学院寒区旱区环境与工程研究所,甘肃 兰州 730000；3.陕西省农业遥感信息中心，陕西 西安 710015)

借助生态位理论，利用地形条件、生产条件、生活条件以及生态条件等17个适宜性评价因子构建秦岭局部山区建设用地适宜性评价指标体系，采用广义相加模型(GAM)、人工神经元网络(ANN)、随机森林模型(RF)以及最大熵模型(MaxEnt)，分别对商洛市商州区建设用地适宜性进行评价，最后以AUC值(ROC曲线下面积) 为权重集成4个模型的模拟结果，定量评价商州区建设用地适宜性。结果表明：商州区最适宜建设用地面积为118.32 km2，占研究区总面积的2.47%，说明该区适宜建设用地开发的土地相对较少；低适宜建设用地面积为297.73 km2，占研究区总面积的7.26 %，可以适度进行开发。生态位模型为秦岭山区建设用地适宜性评价提供了新的方法与途径，也可为当前区域建设用地优化布局提供理论基础。

建设用地；生态位理论；集成模型；秦岭山区

0 引言

生态位是指目标种群在其生存的生态系统中的位置，具体是指其与环境以及其他相关种群之间的功能关系与相互作用[1-3]。由于其实用性和可操作性，生态位理论在学界得到了长足的发展，目前其应用逐渐由生态学领域扩展到城市、旅游、企业发展等领域[4-6]。近年来，越来越多的学者将生态位理论用于土地资源利用研究中，一般将土地利用方式比作物种生态位，而土地利用方式适宜性评价目的就是寻找最适宜生物生存的空间位置[7,8]。本文将秦岭山区建设用地对自然条件以及社会经济条件的需求所构成的n维资源空间称为建设用地资源需求生态位;建设用地的现实自然条件以及社会经济条件也构成对应的资源空间，称为现实资源生态位[9]。现实生态位与需求生态位的耦合关系，表达了现实建设用地条件满足其需求条件的程度，在本文中称之为建设用地生态位适宜度[10]。

秦岭山区是我国南北地理与气候分界线[11]，该区面积广阔，地形地貌复杂，气候条件多变，生态敏感而脆弱，同时该区也是生物多样性热点地区之一[11-13]。近年来随着经济的发展，旅游开发和城镇化建设在一定程度上影响了当地自然的生态过程，使野生物种生境日趋破碎化，种群数量下降。相对地形平缓的平原城镇，秦岭山区建设用地条件特殊，受自然地理条件的制约较大，生态环境脆弱，资源承载能力有限[4]。因此对秦岭山区建设用地进行适宜性评价，对科学指导该区建设用地选择和布局以及协调经济社会发展与生态环境保护之间的关系起着重要作用。

目前国内关于山地建设用地分布研究主要采用传统的相关分析、景观分析以及GIS空间分析等方法[7,10,14]。秦天天等借助生态位理论，利用专家打分法确定评价指标权重，对山地农村居民点进行适宜性评价研究[7]；齐增湘等利用遥感和地理信息技术，从自然环境条件、生态限制条件、社会经济条件三方面构建秦岭山区聚落用地适宜性评价指标体系，采用人为定义因子分级标准，并采用层次分析法(AHP)确定各因子权重值[10]，综合评价了秦岭山区聚落用地适宜性；杨子生将山区城镇建设用地适宜性评价因子分为特殊因子和一般因子两类，采用德尔菲法确定因子权重，并结合“极限条件法”与“适宜性指数法”构建新评价方法，对传统的单一的综合指数法有一定的改进[14]。以上研究为本文提供了一定的理论基础，但其人为因素影响较大，在一定程度上降低了评价结果的客观性。本文以商洛市商州区为例，基于生态位理论，利用非线性回归模型——广义相加模型(Generalized Additive Model,GAM)以及3个机器学习模型——人工神经元网络(Artificial Neural Networks,ANN)、随机森林模型(Random Forest,RF)、最大熵模型(MaxEnt)分别对商洛市商州区建设用地适宜性进行评价，最后以曲线下面积(Receiver Operating Characteristic Curve,ROC)为权重集成4个模型的模拟结果，对商州区建设用地适宜性进行评价研究。本研究构建的建设用地适宜性评价模型利用数据驱动，能够最大限度体现研究区建设用地数值特征，避免主观因素对评价结果的影响。本文的研究结果可以为秦岭地区合理利用土地资源、保护耕地、制定村庄发展建设规划提供参考，为实现区域生态环境的协调和可持续发展提供理论依据。

1 研究区概况与数据来源

商洛市商州区位于秦岭东段南侧腹地，陕西省东南部，是秦岭山区人口、资源、环境矛盾相对集中的地区之一，其地理坐标介于北纬33°38′～34°12′、东经109°30′～110°14′之间。区内地貌类型复杂，山地、丘陵、河谷、平原等地貌类型齐全，自然景观和人文景观汇集，经济的快速发展与生态环境保护之间的矛盾不断激化，严重影响了该区的可持续发展。商州区辖30个乡镇办事处，2013年研究区总人口55.39万人，土地总面积为2 644.36 km2，建设用地面积为82.79 km2占土地总面积的3.13%。目前，商州区是陕西省重点生态保护区和南水北调重要水源涵养基地，该区大部分地区属于限制开发区，经济条件较差，生态基础较好，环境保护意义重大。

本文的研究数据来源于：1)2013年商州区土地利用变更调查数据。该数据依照国土资源部2007 年颁布的《第二次全国土地调查技术规程》(TD/T1014—2007)，将全国土地根据其利用现状进行分类。本研究采用权威土地利用现状数据，可以减少以遥感数据作为数据源解译的人为误差，同时也保证了数据的各类土地利用图斑的空间位置以及图斑面积的精度[15]。2)商州区90 m分辨率的 DEM(数字高程模型)和坡度(SLOPE)、坡位指数(Topographic Position Index，TPI)数据以及30 m分辨率TM数据，来源于地理空间数据云(http://www.gscloud.cn/)。3)商州区土地利用总体规划图(2005—2020)、2013年商州区统计年鉴及社会经济统计资料来源于商州区各相关部门。

2 研究方法

建设用地适宜性评价是科学管理建设用地的基础。本研究评价步骤为:建立评价指标体系，测算各指标实际值，构建商州区建设用地资源现实生态位。随机选择多个现有建设用地中符合要求的点位作为I类采样点(存在点)，同时随机选择多个非建设用地的点位作为II类采样点(不存在点)；利用ArcGIS等软件获取每一个采样点所有评价因子信息，利用不同生态位模型分别总结研究区域建设用地在其生态位中的统计特征，构建评价模型，得到区域条件下建设用地的N维空间集合体;最后在整个研究区应用评价结果，评价其建设用地适宜性。

2.1 建设用地分布点位数据获取

本文将整个研究区划分为106 020个200 m*200 m的网格，选择现有建设用地斑块面积大于40 000 m2的区域作为采样点，共获得323个I类采样，随机选择其中150个采样点进行建模，同时在非建设用地区随机选择300个II类采样点进行建模。

2.2 评价指标体系构建

根据相关研究以及本区建设用地特点，遵循方便性、经济性、永续性及可操作性等原则，参考专家意见，从影响该区建设用地的地形条件、生态条件、生产条件和生活条件中选取具有代表性的16个指标，确立商州区建设用地适宜性评价指标体系[7,10,14,16]。根据商州区建设用地自然条件选取海拔、坡度、坡向、坡位指数作为地形条件的评价指标；生产条件选取到河流的距离、工商业用地可达性、500 0m范围内农用地面积(耕地、园地)以及人均纯收入排名作为评价指标；选取到中心城市的距离、到镇级服务中心的距离、已建成居民点密度、已建成居民点面积、到省道和国道距离、到县道距离以及道路通达性作为生活条件评价指标；选取植被归一化指数(NDVI)、地质灾害以及生态保护区和南水北调重要水源涵养基地作为生态条件的评价指标(表1)。

2.3 评价指标体系测算

本研究中X1(海拔)、X2(坡度)、X3(坡向)以及X4(坡位指数)4个地形条件利用 DEM 分析得到；X5(到河流的距离)、X9(到中心城市的距离)、X10(到镇级服务中心距离)、X13(到省道和国道距离)等距离相关因子采用欧式距离量测每一单元到最近要素的距离，生成200 m*200 m的距离栅格图层；根据文献[17]以及《商州区统筹城乡发展规划》等数据绘制得到X16(地质灾害)；利用网格分析法分别以500 m*500 m为网格单位与农用地(耕地和林地)图斑做叠置分析，统计各个网格内的聚落面积值，然后将该数据与200 m*200 m网格叠置分析，统计属性赋予对应网格，生成X7(500 m范围内农用地面积);同理以200 m*200 m为网格单位与建设用地图斑做叠置分析生成X12(已建成居民点面积)，以商州区建设用地数据为基础，采用密度制图得到200 m*200 m研究区建设用地密度栅格图层；从2013年商州区土地利用变更调查数据提取商州区主要道路数据，采用《城镇土地定级规程》定义的通达度模型，由式(1)计算商州区2013年道路通达度。

表1 建设用地适宜性评价指标与商州区现状值

Y3=[100-100(1-ri)]/100

(1)

式中：Y3为道路通达度，ri为道路相对影响半径,ri=d/di(di为缓冲距离，d为影响距离,d=g/2l)，g为商州区总面积，l为商州区主干道路总长。

乡镇人均纯收入数据采用2013年商州区乡镇人均纯收入排名数据，植被归一化指数(NDVI)利用研究区TM卫星影像获取，生态保护区和南水北调重要水源涵养基地来自于商州区土地利用总体规划图，以上数据处理后均转换为200m*200m的栅格数据。

2.4 空间分布模型

2.4.1 广义相加模型(GAM) 广义相加模型是广义线性模型的半参数扩展[18]，其特点是不强行改变数据的自然度量,数据可以具有非线性和非恒定方差结构，通常适用于数据非线性分布的模型拟合。在本研究中单个因子对于建设用地适宜性的响应曲线由数据分布决定，不指定统一的参数模型。本文通过平滑方法(smoother) 绘制变量响应曲线，为每个变量绘制一条平滑曲线，并将结果相加。GAM模型是基于数据的模型(data-driven),而不是基于模型本身(notmodel-driven),数据决定着响应变量和预测因子之间的关系，而不是假设的响应变量与预测因子间的某种参数关系[19]。本研究中依靠参与建模的采样点位置获取相应的评价指标值，构成17个数据序列，依据数据特征，探索评价指标与现有建设用地分布的非线性关系，以此作为训练，进一步计算整个研究区适宜建设用地的分布。从统计上讲GAM不同于本文中其他模型，它可以显式地表达评价指标与现有建设用地分布的非线性关系。

2.4.2 人工神经元网络(ANN) 本研究在R编程环境下利用BIOMOD软件包进行前馈神经网络(一种输入信号向前传播无反馈的神经网络)的相应计算。本文利用连续单层感应器，构建的前馈神经网络包含输入层、隐藏层(中间层)和输出层，每一层都有若干个节点，前一层和后一层之间靠权值连接。本文主要学习过程为信号的正向传播和误差的反向传播[20]，采用Sigmoid函数作为传递函数。本文BP算法中常用的参数设置如下：通过对学习率η、动量因子α的取值进行运算，确定本文神经网络模型的参数为：η=0.7，α=0.9；通过实验不同初始权、阈值的赋值范围对网络收敛速度的影响，在考虑运算成本以及精度的前提下，确定模型的初始权和阈值的随机赋值范围为-0.5～0.5。参照相关研究，本文确定误差界值Emin为0.0001[21]。本研究中通过训练数据的输入，构建研究区建设用地适宜性评价网络，该网络中I类采样与II类采样点对应的建设用地适宜性值分别为1和0，通过网络的自学习以及不同网络节点的权重调整以达到最优拟合。人工神经网络是经典的机器学习模型，其预测结果精确，但计算量很大。

2.4.3 随机森林模型(RF)RF本质上是一个分类算法，决策树是随机森林模型的基础分类器，由一个独立同分布的随机向量决定其组成。研究采用Breiman的随机森林代码(Fortran),其基本思想是利用Bagging(Bootstrapaggregation，自助聚集)及其原理随机生成大量的分类树参与运算[22]。在本文中评价指标是解释变量，建设用地适宜性是被解释变量。在模型运算过程中每次随机从17个评价指标和450个采样点数据中抽取含9个变量以及不小于200个采样点数据作为单个决策树的训练集。综合评估所有单个决策树结果，取评分最高的分类树作为最后结果。RF是目前应用广泛的机器学习方法，模型在运算量没有显著增大的前提下提高了预测精度。RF对多线性不敏感，预测结果对缺失数据和非平衡的数据比较稳健。

2.4.4 最大熵模型(MaxEnt) 最大熵模型是目前应用最为广泛的基于生态位理论的物种分布模型[23],其基本思想是根据不完全的信息进行统计推断，即根据样本信息对其他未知分布进行最优估计，使其满足样本的统计规则和限制条件，并使该分布满足最大熵的条件。最大熵估计以研究区域不同位置目标事物的概率分布描述事物的真实分布，因此，对于研究区所在空间上每一个位置均对应一个非负概率，最后以事物分布点的背景数据作为限制因子对概率分布进行建模[24]。本研究中只采用I类采样点进行建模，依据有限的适宜建设用地采样点分布信息推断研究区适宜建设用地概率分布。本文采用MaxEnt3.3.3版本，选取75%的分布点作为训练集(trainingdata)，25%的分布点作为验证集(testingdata)。相较其他3种模型，最大熵模型在实现上最为复杂，其优势在于可以将不完整的知识转化成简洁且准确的模型。

2.5 模型评价

本研究采用ROC(ReceiverOperatingCharacteristicCurve,受试者工作特征曲线)评价预测模型的精度。ROC曲线基于非阈值依赖判断(threshold-independentevaluation)模型精度,即以预测结果的每一个值作为可能的判断阈值,由此计算得到相应的灵敏度和特异度。然后以1-特异度(即假阳性率)和灵敏度(即真阳性率)分别为横、纵坐标绘制ROC曲线[25]，ROC曲线与横坐标围成的封闭几何图形的面积值即为AUC(theAreaundertheROCCurve)值，AUC值的大小表征着模型的准确性，值越大说明模型准确性越高，取值范围为[0,1]。

2.6 模型综合

为了更加科学准确地评价商州区建设用地适宜性，本研究综合考虑参与建模的4种生态位模型的精度和稳定性，结合各模型的优点，采用加权平均方法对参与建模的4种生态位模型进行综合。各模型权重由其AUC值归一化确定。计算公式为：

(2)

式中：wj为第j个模型的权重，rj为第j个模型的AUC值，h为模型个数，在本文中取4。

研究区建设用地适宜性综合评价模型计算公式如下[12,13]：

(3)

式中：yi是第i个栅格的建设用地适宜性综合评价指数，wj为第j个模型的权重，xij为第j个模型中的第i个栅格的数值。yi的取值范围为[0,1]，yi越接近1，表明该栅格单元代表的地理空间范围越适宜规划为建设用地。

3 结果分析

3.1 不同模型预测结果的精度比较

本文中4种模型各自的AUC值均显著大于0.5且接近于1，表明这4种生态位模型对商州区建设用地的评价结果都可以接受，将研究区实际建设用地与模型结果做相关性分析(表2)，二者相关性较高，说明模型预测是成功的。4种模型中MaxEnt模型的AUC值最大，说明该模型的预测能力最强，但是综合模型的AUC值比任何单一模型都大，且综合模型结果与实际建设用地的结果相关性更强，因此综合模型的结果更为科学、准确。

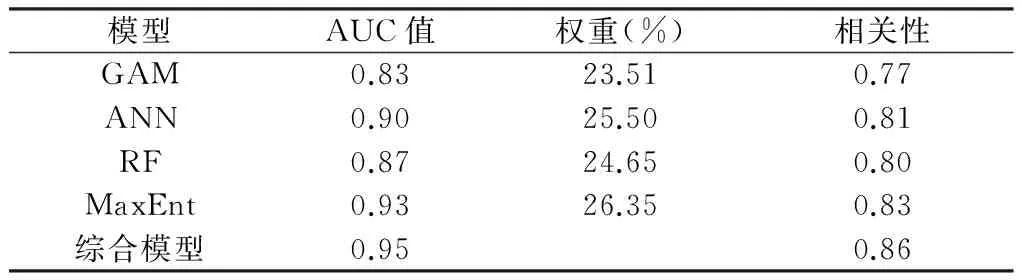
表2 模型AUC值、权重以及与实际建设用地相关性Table 2 The AUC value,weight of the model and correlation with the actual construction land

3.2 评价变量的重要性

根据不同模型的内置算法程序，分别计算了各个评价变量在模型计算过程中的重要性(表3)。综合看4个模型中评价变量的重要性并不相同，但是地形因子(海拔、坡度、坡位指数)在各个模型中均占较大权重。其次是生活条件因子，其中到镇级服务中心距离以及到省道、国道的距离权重普遍较高。研究结果表明，地形以及交通因子是研究区建设用地分布的主要限制条件。

3.3 商州区建设用地适宜性空间格局

本研究中的4种生态位模型对商州区建设用地适宜性评价结果为连续的栅格表面，加权平均后得到的综合模型结果也是连续的栅格表面，其值为 0.03～0.96。按照建设用地适宜性综合评价值从低到高，采用Natural Breaks分级方法将综合模型的结果划分为不适宜建设用地、一般适宜建设用地和高适宜建设用地3类。Natural Breaks[12,13,25]方法基于聚类分析，能较好保持数据统计特性[23]。分级后用地适宜性综合评价指数低于0.328的区域为禁止建设用地，同时在土地利用现状图中提取河流、水库等不适宜建设的区域，也归并为禁止建设用地。适宜指数介于0.328～0.764的地区为一般适宜建设用地，高适宜建设用地的适宜指数等于或大于0.764。同时计算综合模型中各适宜等级的分布面积，得出商州区不同等级建设用地适宜性潜在分布结果(表4)。为便于比较，本文按照相同标准将GAM、ANN、RF及MaxEnt模型结果进行分类，利用ArcGIS 9.3空间分析模块将上述5种模型分级后的结果与研究区行政区域图叠加显示,如图1、图2所示。

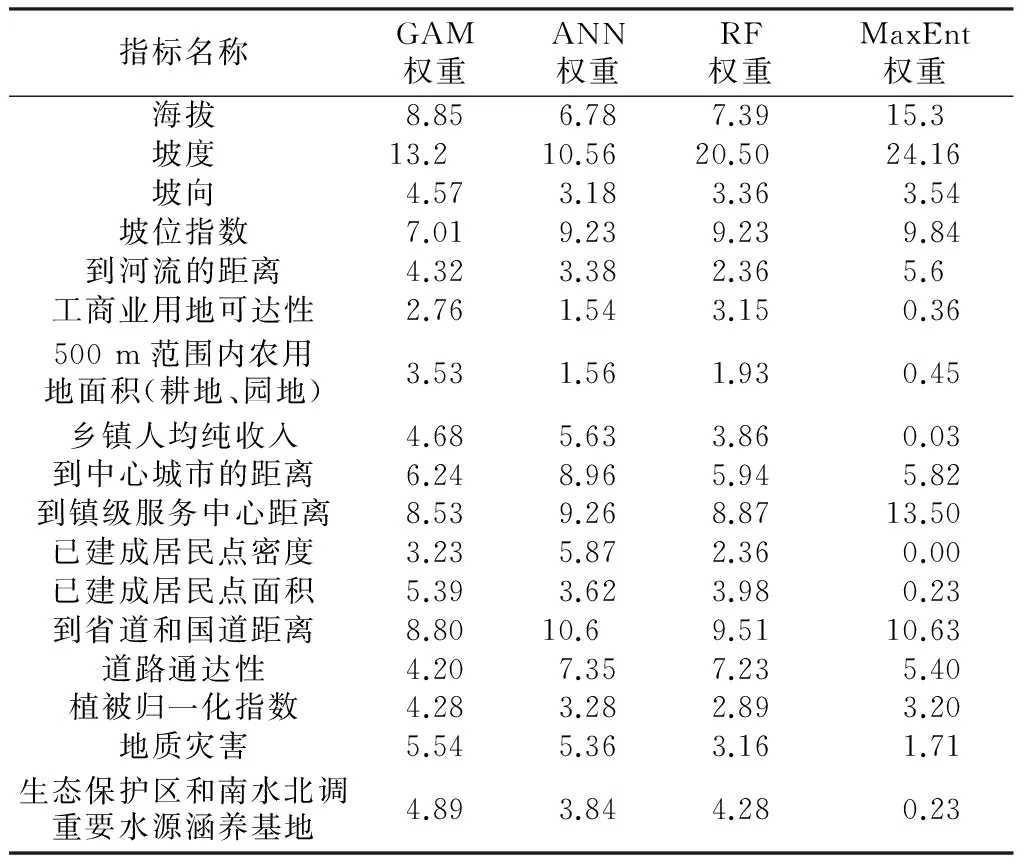
表3 商州区建设用地适宜性评价因子重要性

表4 建设用地适宜性评价综合分析

图1 基于4种生态位模型的商州区建设用地适宜性分级结果

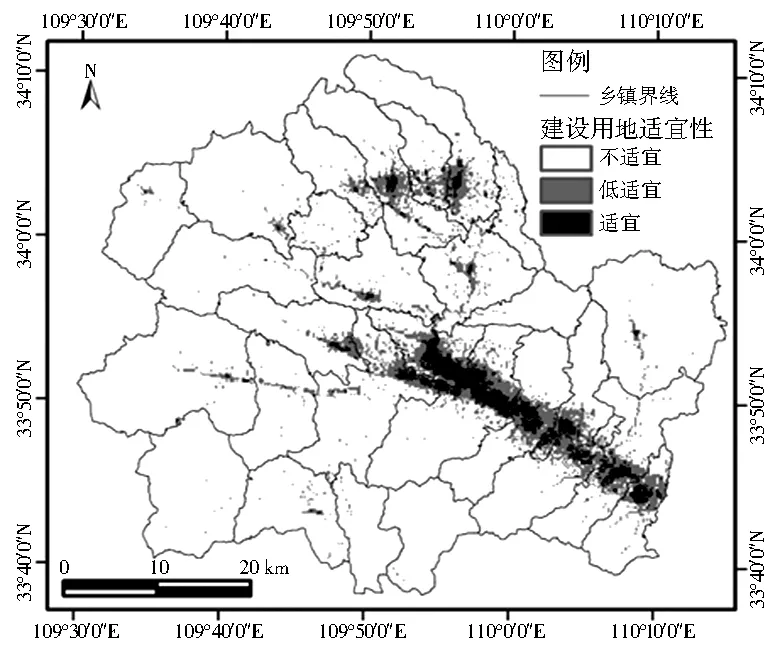
图2 基于综合模型的商州区建设用地适宜性分级结果

结果表明，由于自然条件的制约，商州区最适宜建设用地较少，只占其面积的 2.47%，主要分布于丹江及其主要支流两岸，包括陈塬以东至孝义，以及杨峪河、大荆、腰市、李庙等地的川道和两侧坡塬。该地区地势平坦，交通便捷，自然地理条件优越，同时也是商洛市市区所在地，基础服务设施齐全，人口密集，经济水平较高，是未来商州区建设用地的主要发展方向。一般适宜建设用地面积相对较大，为297.73 km2，主要分布于适宜建设用地周边低山区，同时在研究区北部的腰市镇、大荆镇、李庙乡以及西荆乡也有一定分布，这些地区地形较为平坦，离水源地较近，离较大的乡镇服务中心距离适中，基础服务设施完善，交通便利，生活和生产条件相对优越，建设用地具有一定的发展潜力。

商州地貌是东秦岭山地地貌的组成部分，是一个结构复杂的以中、低山体为主的土石山区，境内地貌复杂、山系纵横，主要山系有位于研究区西北的秦岭主脉，研究区北部的蟒岭，南部的流岭，以及研究区中部的熊耳，构成了北、西、南三面高耸，向丹江河谷倾斜的趋势，因此不适宜建设用地占研究区总面积较大。经计算，商州区90.27%的区域不适合建设用地开发，主要包括以下两种地貌类型：1)低山丘陵地貌区。该区为复合地貌类型，主体位于境内北部和东北部及中部的广大地区;其农业生产条件较差，风化强烈，自然坡面坡度较大，植被稀少，水土碎石流失较为严重。对该区建设用地建议维持现状，同时加强对其周边一般适宜建设用地以及最适宜建设用地社区的基础服务设施，尤其是教育设施的财政投入，引导人口外迁，逐步减少居民点建设面积，使其自然衰退。2)中高山地区。该区分布于境内西北部和西部秦岭南翼，西南部和南部的流岭，东北部的蟒岭;其自然坡面坡度多在30°以上,耕地分布于梁、洼、槽及沟道，陡坡地所占数量很大，是弃耕还林还牧的重点地区。该区地质灾害多发，交通不便，人口稀疏，优质农业资源较少，不适宜居民点建设，应作为重点生态保护区域。

4 结论与讨论

建设用地适宜性评价研究是社会建设的实际需求，也是我国城镇化过程中居民点以及公共设施优化布局的理论基础。本文运用4种生态位模型，以商州区建设用地适宜性评价为切入点，以GIS空间分析技术为支撑，对商州区建设用地适宜性进行了多因素综合适宜性评价，并应用加权平均方法构建综合模型，采用系统聚类方法，将商州区建设用地适宜性划分为3种类型。分析结果表明，受生态条件、生活条件、生产条件限制，商州区建设用地适宜度分布具有明显差异，该区大部分区域不适合建设用地分布，最适宜建设用地主要分布于丹江及其主要支流两岸，该区域应加快最适宜建设用地区域建设和中高山地区居民点搬迁与撤并工作，在此基础上，逐渐开展一般适宜建设用地的集中建设。

科学的建设用地适宜性评价体系与方法，将为地区土地利用总体规划以及村级规划提供理论依据。生态位理论是生态学重要的基础理论，其方法不仅能广泛应用于自然生态系统，而且对于社会、经济生态系统也具有重要意义。本文将其理论与方法引进建设用地适宜性评价中，进行了有益的探索，各种模型在较大程度上规避了主观因素对评价结果的影响，取得了较好的效果，对经典生态位理论的深化和发展具有一定意义。但是，通过生态位理论与多模型相结合的方式进行建设用地适宜性评价尚属尝试，且决策者的主观意愿表现不足，那么如何在评价因子中加入一定的地域特点和政策制度等因素还有待进一步研究。

[1] AUSTIN M P.Spatial prediction of species distribution:An interface between ecological theory and statistical modeling[J].Ecological Modelling,2002,157(2/3):101-118.

[2] SOBERON J,PETERSON A T.Interpretation of models of fundamental ecological niches and specie′s distributional areas[J].Biodiversity Informatics,2005(2):1-10.

[3] HIZEL A H,LE LAY G.Habitat suitability modeling and niche theory[J].Journal of Applied Ecology,2008,45(5):1372-1381.

[4] 欧阳志云，王如松，符贵南.生态位适宜度模型及其在土地利用适宜性评价中的应用[J].生态学报，1996，16(2):113-120.

[5] 瘳红娟，徐建华，岳文泽.城市生态系统适宜度的时空对比分析[J].生态科学，2003，22(4):300-304.

[6] 钱辉，张大亮.基于生态位的企业演化机理探析[J].浙江大学学报(人文社会科学版)，2006,36(2):20-26.

[7] 秦天天，齐伟，李云强，等.基于生态位的山地农村居民点适宜度评价[J].生态学报，2012, 32(16):5175-5183.

[8] 蒙莉娜，郑新奇，赵璐，等.基于生态位适宜度模型的土地利用功能分区[J].农业工程学报,2011，27(3):282-287.

[9] 许仲林，彭焕华，彭守璋.物种分布模型的发展及评价方法[J].生态学报，2015，35(2):557-567.

[10] 齐增湘，廖建军，徐卫华，等.基于GIS 的秦岭山区聚落用地适宜性评价[J].生态学报，2015，35(4):1274-1283.

[11] 康慕谊，朱源.秦岭山地生态分界线的论证[J].生态学报，2007，27:2774-2784.

[12] LU C Y,GU W,DAI A H，et a1.Assessing habitat suitability based on geographic information system (GIS) and fuzzy:A case study of Schisandrasphenanthera Rehd.et Wils.In Qinling Mountains,China[J].Ecological Modelling,2012,242(3):105-115.

[13] 郭彦龙，顾蔚，路春燕，等.基于五味子甲素与乙素的秦岭地区野生华中五味子的潜在空间分布[J].植物学报，2013，48 (4):411-422.

[14] 杨子生.山区城镇建设用地适宜性评价方法及应用——以云南省德宏州为例[J].自然资源学报，2016(1):64-76.

[15] 吴江国，张小林，冀亚哲，等.县域尺度下交通对乡村聚落景观格局的影响研究—以宿州市埇桥区为例[J].人文地理，2013，28:110-115.

[16] 曲衍波，张凤荣，姜广辉，等.基于生态位的农村居民点用地适宜性评价与分区调控[J].农业工程学报，2010，26(11):290-296.

[17] 张晓虎，寇泓.陕西省商州区地质灾害成因及防治研究[J].水土保持通报，2008,28(5):195-200.

[18] HASTIE T J,TIBSHIRANI R J.Generalized Additive Models[M].London:Chapman and Hall,1990.

[19] THOMAES A,KERVYN T,MAES D.Applying species distribution modelling for the conservation of the threatened saproxylic Stag Beetle(Lucanuscervus)[J].Biological Conservation,2008,141(5):1400-1410.

[20] O′HANLEY J R.Neural ensembles:A neural network based ensemble forecasting program for habitat and bioclimatic suitability analysis[J].Ecography,2009,32:89-93

[21] 杨广斌.动态数据驱动的林火蔓延模拟系统关键技术研究[D].北京：中国林业科学研究院，2008.80-120.

[22] BREIMAN L.Random Forests.Machine Learning[M].London:Chapman and Hall,2001

[23] YANGA X Q,KUSHWAHAB S P S,SARANB S，et a1.Maxent modeling for predicting the potential distribution of medicinal plant,JusticiaadhatodaL.in Lesser Himalayan foothills[J].Ecological Engineering,2013,51:83-87.

[24] PHILLIPS S J,ANDERSON R P,SCHAPIRE R E.Maximum entropy modeling of species geographic distributions[J].Ecological Modelling,2013,190(3-4):231-259.

[25] 王运生，谢丙炎，万方浩，等.ROC曲线分析在评价入侵物种分布模型中的应用[J].生物多样性，2007，15(4):365-372.

Multi-model Suitability Assessment of Construction Land in Tsinling Mountains Based on the Niche Theory:A Case Study of Shangzhou，Shangluo

ZHANG Hai-long1,GUO Yan-long2,GAO Bei3

(1.CollegeofUrban,RuralPlanningandArchitecturalEngineering,ShangluoUniversity,Shangluo726000；2.ColdandAridRegionsEnvironmentalandEngineeringResearchInstitute,CAS,Lanzhou730000；3.ShaanxiProvincialRemoteSensingInformationCenterforAgriculture,Xi′an710015,China)

Based on the niche theory,the paper uses 17 suitability evaluation factors:terrain conditions,production conditions,living conditions and ecological conditions to build suitability evaluation system of construction land in Tsinling Mountains.Using GAM,ANN,RF and MaxEnt,the paper evaluates the suitability of construction land in Shangzhou district,Shangluo respectively.Finally,simulation result of four models that is weighted by AUC value (area under the ROC curve) is integrated.And it is quantitatively used to evaluate the suitability of construction land in Shangzhou.The result shows that niche model can better evaluate the suitability of construction land in Tsinling Mountains.In an overall view,the most suitable land for construction area is 118.32 km2in Shangzhou,accounting for 2.47% of the total area,indicating that the area of land suitable for the development of construction land is relatively small.In Shangzhou,then,low suitable land for construction area of 297.73 km2in the area,accounting for 7.26% of the total area.This can be appropriate for development.The paper objectively evaluates the suitability of construction land in Shangzhou,providing new ways for the suitability evaluation of construction land in Tsinling mountains.It provides a theoretical basis for optimizing the layout of construction land as well.

construction land;niche theory;integrated mode;Tsinling Mountains

2016-03-03；

2016-05-17

陕西省教育厅专项科研计划项目(15JK1231)

张海龙(1982-)，男，硕士，讲师，主要研究方向为空间数字模型与GIS 应用研究。E-mail：hlsanfx@sina.com

10.3969/j.issn.1672-0504.2016.04.014

F301.23

A

1672-0504(2016)04-0083-07