有害物品运输网络设计与运输路径优化研究
魏 航,钟智龙,陈 静
有害物品运输网络设计与运输路径优化研究
魏 航,钟智龙,陈 静
(上海财经大学国际工商管理学院,上海 200433)
由于在有害物品运输过程中存在巨大的危害,为了降低有害物品运输风险,政府可以通过设立分流设施对有害物品运输车辆进行分流控制,来约束和控制有害物品运输车辆的行车路径,使其避开事故高发路段和人口密集区域,来达到降低风险的目的。首先,对“多起点”-“多终点”有害物品运输中的分流控制问题进行了描述,建立了以总风险最小化为目标的有害物品运输车辆分流控制双层模型,模型的首层为分流设施的选址与关闭路段的选择问题,第二层为给定关闭路段的运输网络下每辆有害物品运输车辆的路径选择问题。然后,利用KKT条件将双层模型转化为单层整数规划,并将非线性约束转化为线性约束。最后,给出了一个算例,算例表明分流设施的设置能够非常有效地降低有害物品运输带来的风险。
有害物品运输;网络设计;风险;路径控制
0引言
有害物品(hazardous materials) 是一种具有物理、化学或是生物特性的物品,它容易在生产、储存、运输中引起燃烧、爆炸、中毒等灾害事故,对周围的人口、环境和财产会产生一定的危害。有害物品主要包括:爆炸品、氧化剂、压缩气体和液化气体、易燃液体、易燃固体、遇湿易燃和自燃物质、毒害品、放射性物品、腐蚀性物品等[1]。
对于正处于工业化发展的中国来说,有害物品的生产量和运输量均在逐年增加,有害物品对人们和环境危害正在扩大和加深。根据统计,在中国仅液氯的年流动量就已经达到170多万吨,液氨的年流动量达到80多万吨[2][3]。由于有害物品的特殊性状,可能会引发重大事故,使群众生命财产遭受重大损失,仅仅从2002到2004年,我国共发生了1091起有毒气体泄漏事故,累计造成977人死亡,有1477人在事故中受伤,8695人中毒[4]。
因此,在有毒有害物品生产、运输、仓储等环节中,对如何降低事故的发生进行了大量的研究和实践。这些研究主要集中在网络设计[5][6]、路径选择[7][8]、合理选址[9][10]、风险度量[11]、操作规范等方面,以及在发生事故之后的应急疏散[12]。
特别地,由于生产地和使用地点的分离,大多数有害物品往往不是在它们的生产地点被使用,而是需要经过较长距离的运输才被使用或处置,我国95%以上的危险化学品涉及异地运输问题。其次,从运输量来看,有害物品运输占我国年货运总量的30%以上,道路有害物品年运输量约在1~2亿吨,其中剧毒氰化物类就达几十万吨,易燃易爆油品类达到1亿吨错误!未定义书签。。特别地,随着我国经济的发展,有害物品运输并呈上升趋势,长距离、大吨位已成为我国有害物品道路运输的普遍状况[3]。
基于如此巨大的运输量以及众多的运输任务,在有害物品事故中,由交通引起的事故的比例相对较高,有害物品运输中引起的事故约占有害物品总事故数的41%[4]。近年来我国连续发生多起恶性交通运输事故,比如:1 2004年1月13日,河南省西郑高速公路上,一辆液氯槽罐车发生泄漏,约2.4万人紧急疏散。22005年3月29日,在京沪高速公路上,一辆载有约40吨液氯的槽罐车与一辆货车相撞,导致液氯大面积泄漏,中毒死亡者达28人,送医院治疗285人,组织疏散村民群众近1万人,造成京沪高速公路宿迁至宝应段关闭20个小时,受灾农作物面积达20620亩,畜禽死亡15000头(只),总损失近2000千万。32005年3月17日,河南省一辆货车非法偷运6吨黑火药,发生爆炸,造成31人死亡8人受伤。4 2008年11月19日,广州一辆装载约21吨的液化石油气的槽罐车发生侧翻,造成罐体内的液化石油气发生泄漏,并引起大火,火灾持续了42个小时,事故造成高速公路封路,损失估计超过千万元。
因此,如何降低有害物品运输中的风险吸引了众多学者进行了大量的研究,目前大多数研究主要致力于获得同时考虑风险和成本的最优路径。这些研究均假设有害物品的承运商在选择路线时会考虑有害物品运输风险,其选择路径是基于成本和风险权衡之后获得的结果。
然而,在现实中,由于有害物品事故发生率较低(约为10-4.公里~10-5.公里),大多数承运商往往忽略了风险的考虑,主要从成本最小化的目标出发选择运输路径[5]。这种基于最小成本的路径选择方式,可能使得运输车辆选择某些具有较高人口密度的路段,使得大量的有害物品运输车辆通过这些路段,导致这些路段上的风险剧增,进而可能引发恶性事故,导致大量的人员伤亡。因此,需要从这种现实的情况出发,考虑通过对有害物品运输车辆的行车路径进行限制,禁止某些车辆通过风险较高的路段,或是分流一部分有害物品运输车辆到某些低风险的路段,以达到降低风险的目的。
由于对于运输车辆运输过程进行全程监控成本太高,且非常困难。同时,在进行路段控制时,由于起点和终点的多样性,需要针对每辆车设计其具有个性的路段。因此,可以考虑在有害物品运输网络中设立一定数量的分流设施,并通过分流设施对有害物品运输车辆进行分流控制,来约束和控制有害物品运输车辆的行车路径,使其避开事故高发路段和人口密集区域,来达到降低风险的目的。对于有害物品运输车辆分流问题,主要涉及到路线选择、网络设计、设施选址、交通分流等方面,因此,对于有害物品运输车辆分流问题的文献评述也将从这几个方面展开。
首先,对于有害物品运输中路线选择方面,Erkut和Alp错误!未定义书签。在允许有害物品运输车辆暂停的条件下,给出了有害物品运输的路线选择策略,以降低有害物品运输的风险。Nozick, List和Turnquist[8]对有害物品运输中车辆的运输路径和车辆调度问题进行了研究,给出了求解的算法。魏航[13]对时变网络下有害物品运输路径选择进行了研究,分别在多式联运、有宵禁限制和有公平性限制下设计了求解的算法。魏航[14]对时变随机网络下有时时间窗限制的有害物品运输路径进行了研究,利用标号法给出了求解的算法。张敏等[15]研究了危险品物流系统中的选址-选线问题,建立了基于路网危险度瓶颈限制的危险品集成物流系统选址—选线的多目标模型,给出了一种启发式算法。
其次,对于有害物品运输网络设计方面,Kara和Verter[16]从政府角度出发,认为承运商选择的路径是基于成本最小化作出选择,考虑在有害物品运输网络中,通过关闭若干路径来达到降低总风险的目的。Kara和Verter[5]在给定车辆行走的线路的基础上,给出了进行有害物品运输网络设计的模型和方法。Marcotte, et al[17]考虑通过不同的收费来限制和控制有害物品运输车辆的运输线路,给出了求解的启发式算法。
第三,对于离散网络下的设施选址问题,Daskin[18]对与离散网络下设施的选址问题进行了研究,给出了在各种情况下的选址模型以及相应的算法。Drezner[19]对与离散网络和连续平面下设施的选址问题进行了研究和评述,也给出了在各种情况下的选址模型以及相应的算法。ReVelle和Eiselt[20]对目前关于选址问题已有的研究进行了评述,并提出了未来发展的方向。特别地,王刊良,徐寅峰[21]针对有害物品的运输网络中分流设施设置的问题,建立了系统效率模型,从而使得大多数运输有害物品的车辆尽可能早地接受检查。
最后,对于交通分流问题和分流设施设定方面,Merchant和Nemhahuser[22][23]最早对动态网络流分配问题进行研究,将时间划分为若干段的情况下,设计了求解的算法。Yang和Zhou[24]较早提出了在指定分流设施的数目下的选址标准,建立了在运输网络中对所有的流量分流设施选址的模型,这些模型假定分流设施是设立在网络的节点上。之后,在文献[22][23]的基础上,对动态交通流分配问题进行了大量的研究,Peeta和Ziliaskopoulos[25]对已有动态交通流分配问题进行了综述,并提出了未来的研究方向。
但是,关于如何合理选择有害物品运输车辆的分流设施,以及分流设施应该如何控制相应的路段,来减少有害物品运输所造成的风险,这一问题还没有进行深入的研究。因此,本文对“多起点”-“多终点”有害物品运输车辆的分流设施选址与分流控制问题进行了研究,对“多起点”-“多终点”有害物品运输中的分流控制问题进行了描述,建立了以总风险最小化为目标的有害物品运输车辆分流控制双层模型,模型的首层为分流设施的选址与关闭路段的选择问题,第二层为给定关闭路段下每辆有害物品运输车辆的路径选择问题。然后,利用KKT条件将双层模型转化为单层整数规划,并将非线性约束转化为线性约束。最后,给出了一个算例,算例表明分流设施的设置能够非常有效地降低有害物品运输带来的风险。
1基本分析
对于有害物品运输分流控制,包含政府与承运商两个主体。其中,①进行分流设施选址和分流控制的主体为政府管理部门,其主要目标为降低有害物品运输风险;②承运商在给定的允许进行有害物品运输的网络中选择合理的运输路径。因此,有害物品运输分流控制需要解决的基本问题为:给定一个离散的运输网络,在若干起点和终点之间进行有害物品运输,现需要在网络中选择若干节点作为分流设施设定点,并决定有害物品运输中与分流设施点相连的路段的关闭与开放情况,以最小化有害物品运输风险①。为了有效地阐述和分析有害物品运输分流问题,下面将分别对解决问题的基本思路、分流设施的控制机制,以及分流控制模型三个方面进行分析和说明。
1.1 基本思路
在以往大多数有害物品运输的研究中,学者们致力于寻找出同时考虑运输风险、运输成本等多目标的最优路径。通常,如果以降低总风险为目标,一般的做法是将有害物品运输成本的作为限制条件,即通过找到每辆车的最小化风险的行车路径来降低总风险。
而在现实生活中,有害物品的运输存在着两种不同的主体:政府和承运商。其所考虑的目标不同:政府关心的是有害物品运输所带来的(潜在)风险大小;而承运商更加注重运输成本的大小。因此,承运商为了追求成本的最小化,通常会忽视对风险的考虑,选择成本较低的路径,这样往往会带来严重的后果。这样,以往传统的研究中,成本约束下风险最小化的目标就失去了作用。因此,对于政府而言,为了降低有害物品运输对公众和环境的影响,可以对承运商的路径选择进行约束和控制,使其避开事故高发路段和人口密集区域,以达到降低风险的目的。
为了降低有害物品运输风险,Kara和Verter[16]研究了有害物品运输网络设计优化研究,其也考虑从政府的角度,对每一种有害物品选择关闭合理的有害物品运输路段。但是,这样的网络设计需要全程监控有害物品运输车辆、大规模地关闭有害物品运输路段,这给社会带来了巨大的成本②。
然而,若是在网络中设立一定数量的设施,通过这些设施针对每一个“起点”-“终点”之间的运输任务,控制和分流有害物品运输车辆,只需要改变少量的运输路段,就可以有效降低有害物品运输风险。这样,有害物品运输分流的基本思路是:站在政府角度,通过设立分流设施,并对途经分流设施的有害物品运输车辆的进行分流控制,并对不同车辆关闭特定的路径,限制和改变运输有害物品车辆的原有行车路径,达到风险降低的效果。
1.2 分流控制机制
根据有害物品运输分流的基本思路,需涉及到3个方面的问题,分别是:分流设施的设点问题、分流设施的分流控制问题和承运商合理选择路线问题,具体按如下过程进行:①在给定的运输网络中,选择合理数量的分流设施;②分流设施根据分流设施的位置,以及有害物品运输车辆的起点和终点,决定禁止有害物品运输车辆通行的路段;③承运商在开放路段形成的运输网络内,根据自己的利益或偏好做出反应,选择合理的行车线路(在此,假设承运商以成本最小化为目标,即按最短路行车)。显然,不同的设施选址点,以及不同有害物品运输车辆通行路段的关闭情况,均会影响最终有害物品运输的总风险。因此,分流设施的设定与关闭路段的选择,需要根据承运商的对策,调整自己的决策,以最小化有害物品运输风险。
可见,分流控制受到分流设施和承运商的共同影响。但同时,分流设施和承运商也具有相对的独立性,即:①分流设施只能对有害物品运输车辆可能通过的路段加以限制来影响承运商的路径选择,却不能直接干涉承运商在允许通过网络内的具体路径选择;②承运商也只需把分流设施的限制作为参数或约束条件,其可以在可能的范围内自由决策。
1.3 分流控制模型
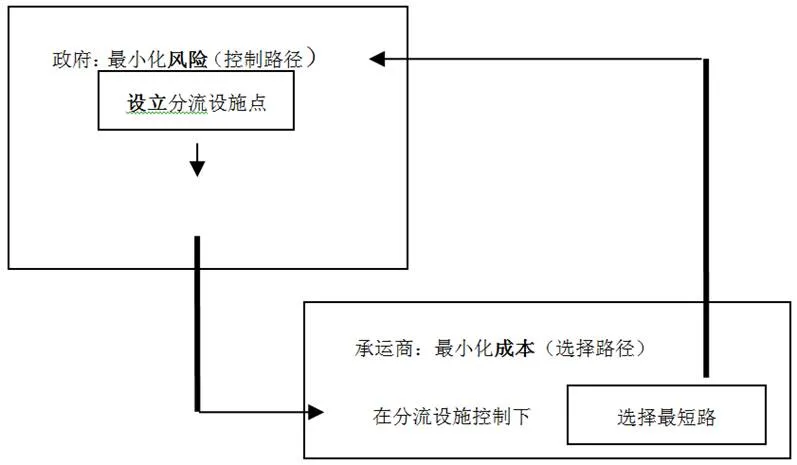
图1 有害物品运输分流控制的双层规划结构模型
因此,有害物品运输分流控制问题是一个典型的双层规划问题。代表政府的分流设施在系统中处于领导地位,其决策属于上层规划问题,需要决定分流设施的选址以及路段的关闭情况。承运商则出于跟随者的地位,其决策属于下层规划问题,需要根据网络的开放情况,选择合理的行车线路,具体如图1所示。
2 问题描述
一般地,对于有害物品运输车辆分流控制问题,可以描述为:设有害物品的运输网络为,其中,为结点集,代表路段(有向边)的集合。设为路段的距离,在路段上运输第种有害物品的风险,。网络中存在辆车进行有害物品运输,其各自的起点与终点分布为与,运输的有害物品种类为,。为了降低有害物品运输风险,可以在网络中选择个节点设置分流设施,为在节点设置分流设施的成本,,设施设立的总成本不能超过。对于存在分流设施的节点,允许分流设施对可能经过分流设施的车辆的下一个路段进行关闭或开放。现需要在网络内选择合理的节点设置个分流设施,并对每辆运输有害物品的车辆选择合理的路段进行关闭,使得有害物品运输风险最小,。
3 数学模型
为了得到有害物品运输车辆分流控制问题模型,定义如下变量:
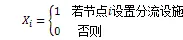
这样,有害物品运输车辆分流控制模型可以描述为:
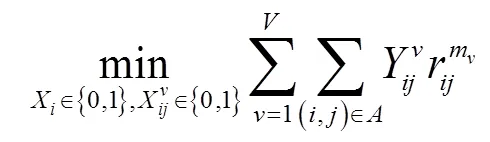
s.t.(2)
(3)
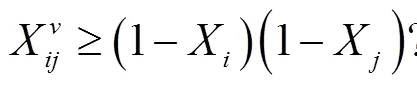
其中,是的解。 (5)
(6)

(8)
其中,约束(2)保证了选择分流设施的数量;约束(3)为成本约束;约束(4)表示政府只能在包含存在分流设施路段中选择是否进行关闭,即当和同时为0时,,即如果节点和都未设分流设施,路段开放,可供车辆任意行驶;而当和不同时为0时,,此时,分流设施可以选择对车辆关闭路段;约束(5)是承运商的最短路目标函数;约束(6)是流量平衡约束,保证选择的路径为起点到终点之间的可行路径;约束(7)表示运输车辆在路段能够通行与否,需要满足政府对此路段的开放与否的约束;约束(8)是0-1约束。
4 模型转换
显然,有害物品运输分流控制问题为双层规划问题,具有较高的计算复杂性。为了方便求解,下面将分别首先对双层规划进行了单层化,然后将非线性约束的线性化,降低问题的求解难度。
4.1 模型单层化
显然,根据给出的数学模型,该模型为一个双层模型。模型下层规划是一个0-1整数规划,上层规划是一个非线性0-1整数规划。如果给定上层决策变量和的值,下层规划就变成车辆的最短路问题,容易求得的值。如果给定下层规划的决策值,即,上层目标函数值也能被确定,但问题的关键是和相互作用,使得该问题的计算复杂性很高。根据Garey, Johnson的研究,一般的选址问题均为NP-难题[26]。本问题的上层问题为一个选址问题,下层问题为一个最短路问题,因此该问题也成为一个NP-难题。
对于双层规划问题的求解方法,Bard对双层规划问题的求解方法进行了总结[27]。一般地,对于线性的双层规划(更一般地,可以只要第二次规划问题为凸包问题就可以),可以利用KKT条件将双层规划转换为单层规划问题。对照KKT条件发现,根据给出的双层规划问题,根据Wolsey的证明[28],一旦给定,那么第二层规划问题就变为幺模问题(unimodular)。因此,约束(8)可以被所替代,且不影响其最优解的获得。因此,第二层问题可以松弛表达为一个线性规划问题,其承运商的目标函数是严格凸函数,约束条件均为线性,故存在最优解,且KKT条件是最优解的充要条件。因此,模型中的下层规划的最优解可由式(6)-(8)和KKT条件求得,其中KKT条件如下:

(9)
(10)
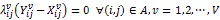
,为自由变量,(12)
这样,原来的双层规划就变为以上层规划目标函数为目标函数,与上层约束条件和下层规划KKT条件为约束条件的单层规划。但是,由于之前进行KKT条件转换的时候,是在一旦给定的情况下具有的幺模性质。而当其为单层规划时和同时作用,使得此时不具有幺模性质。因此,需要把约束(8’)用(8)重新进行替代,保证其整数的约束。由此,有害物品运输车辆分流控制模型可以表示为:

s.t. (2)-(4), (8), (9)-(12) (14)
这样,经过模型转换,得到的模型是一个0-1整数规划。
4.2 约束线性化
由于给出模型中的约束(4)、(10)和(11)为非线性约束,因此,需要对其进行线性化。对于约束(10)和(11),根据Kara和Verter[16]的研究,可以改为:
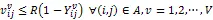
(16)
其中,是一个特别大的数值。
其次,约束(4)也是一个非线性约束,其表达的意义为决策变量需要满足或。由于、和为0-1变量。因此,约束(4)可以简化为线性约束,。对于约束(4),由于和已经存在0-1整数约束,其需要保证的仅仅是当时(不允许车辆通过)在节点或节点上必定存在分流设施。即当时,必定存在或。对于约束(4)存在四种情况且线性约束具有完全的等价性:i) 当且时,可以取0或1,新约束为,等价;ii) 当且时,可以取0或1,新约束为,等价;iii) 当时,新约束为,但是由于有的约束存在,因此,的取值仍然为0或1,等价;iv)当时,的取值为1,表示可以通过路段,新约束为,等价。
这样,模型可以表达为如下形式:
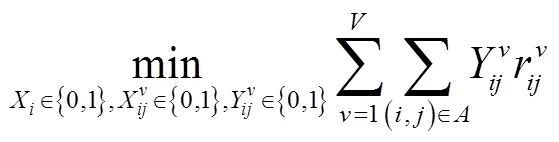
s.t.(18)
(2)-(3), (8), (9),(12), (15), (16) (19)
这样,就可以将有害物品运输分流控制模型转换为线性规划,可以利用CPLEX进行求解。
5 算例
5.1 算例描述
在此,以图2为例来说明分流设施在有害物品运输风险控制中的应用。图2是华北和华东的部分交通图,研究中通过对运输网络的简化,考虑网络中的重点城市,这些城市分别为:济南、济宁、青岛、日照、连云港、徐州、淮安、扬州、盐城、南通、南京、常州、无锡、苏州、蚌埠、合肥、芜湖、湖州、嘉兴、上海。将这些城市和路线进行抽象,可以得到如图3的运输网络图,该运输网络由20个节点,35条路段组成。

图2交通运输体系地图
对于图3中有害物品运输的基本情况,表1给出了各条路段发生事故的概率(10-4.公里)、周围的人口密度(人/公里2)以及路长(公里)①,表2给出了各起点和终点之间有害物品的运输量(万吨),车辆的核定载重为10吨。对于给出的4种有害物品中,盐酸为易制毒品,液氯为剧毒化学品,烧碱、邻甲苯胺都为普通危险品;因此,设各种有害物品发生事故后的致命率分别如下:盐酸为0.0001、液氯为0.0005、烧碱为0.00003、邻甲苯胺为0.00005。同时,设各种有害物品对于路径两侧人口的影响距离为0.5公里。
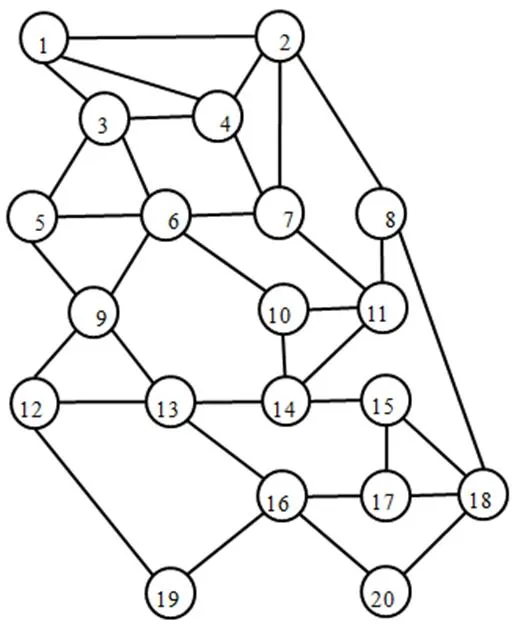
图3交通运输网络图
表1路段发生事故的概率、人口密度以及路段长度

(i, j)(1,2)(1,3)(1,4)(2,4)(2,7)(2,8)(3,4)(3,5)(3,6)(4,7)(5,6)(5,9) 122211333233 300606027013025050100110120140180 6896896896281092628689689689827827689 (i, j)(6,7)(6,9)(6,10)(7,11)(8,11)(8,18)(9,12)(9,13)(10,11)(10,14)(11,14)(12,13) 455631121015122 8013020016050450120130503090140 328868932883288827827387387328810921092387 (i, j)(12,19)(13,14)(13,16)(14,15)(15,17)(15,18)(16,17)(16,19)(16,20)(17,18)(18,20) 15281811712112 2501501708013019090180230130170 30410923041092489489489304489489489
表2 各条路径的有害物品运输

起点-终点o-d盐酸(H)液氯(CL)烧碱(N)邻甲苯胺(C)总计 济南-上海1-202730.512.5 青岛-合肥2-190.2230.24.4 青岛-上海2-200.80.550.36.6 济南-合肥1-1911.5417.5 总计41015231
5.2运算结果
显然,分流设施的数量对分流设施的选择、路线选择以及分流有着重要的影响,下面将分别给出了具有0、1、3、5和20个分流设施下,最优分流设施的位置,以及不同“起点”-“终点”之间有害物品运输车辆的行车路线,并与无分流设施下的行车线路进行了对比。
5.2.1不设置分流设施的方案
当不设施分流设施时,按照承运商以最小成本为选择路线的准则,各个“起点”-“终点”之间运输有害物品的车辆以最短路行驶,各条运输线路分别如图4所示,表示各条行车路径。同时,各“起点”-“终点”之间的距离和风险值,以及完成运输任务所需的总路径与总风险分别如表3所示。显然,不进行分流设施设置的情况,为后面进行分流设施设置方案提供了基础的比较对象。

表3 不设置分流设施的方案的计算结果
5.2.2 设置1个分流设施的方案
1-19/19-1 车辆行驶路径对比图 1-20/20-1 车辆行驶路径对比图 2-19/19-2 车辆行驶路径对比图 2-20/20-2 车辆行驶路径对比图

设有分流设施的节点原行车路径控制后行车路径分流设施选择关闭的路段 图5设1个分流点的情况下有害物品车辆行车路径示意图
表4 设置1个分流设施的方案及计算结
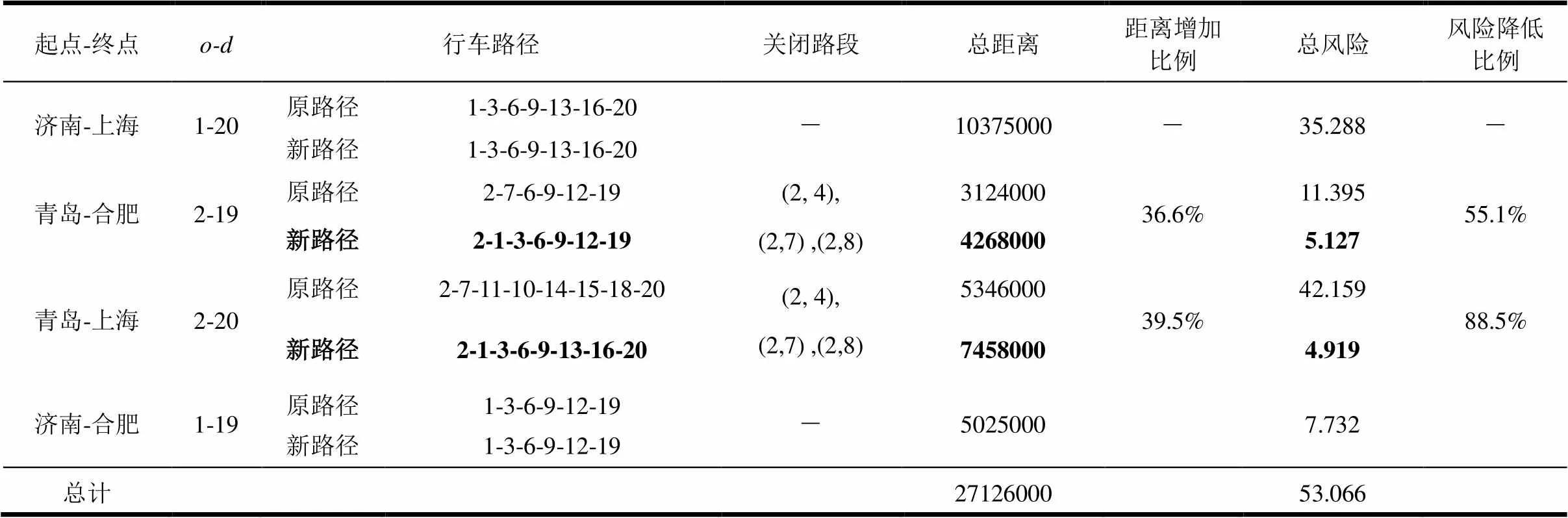
起点-终点o-d行车路径关闭路段总距离距离增加比例总风险风险降低比例 济南-上海1-20原路径1-3-6-9-13-16-20-10375000-35.288- 新路径1-3-6-9-13-16-20 青岛-合肥2-19原路径2-7-6-9-12-19(2, 4), (2,7) ,(2,8)312400036.6%11.39555.1% 新路径2-1-3-6-9-12-1942680005.127 青岛-上海2-20原路径2-7-11-10-14-15-18-20(2, 4), (2,7) ,(2,8)534600039.5%42.15988.5% 新路径2-1-3-6-9-13-16-2074580004.919 济南-合肥1-19原路径1-3-6-9-12-19-50250007.732 新路径1-3-6-9-12-19 总计2712600053.066
在设置1个分流设施的成本约束下,根据给出的模型,可以得到最优的分流设施位置在节点2,各个“起点”-“终点”之间各条运输线路分别如图5所示。同时,分流设施对于相连路段的关闭情况分别如图5所示,分别为(2, 4)、(2,7)和(2,8)。还有,经过设立1个分流设施之后,各个“起点”-“终点”之间有害物品运输的风险与行驶距离分别如表4所示。
5.2.3 设置3个分流设施的方案
在设置3个分流设施的成本约束下,根据给出的模型,可以得到分流设施位置在节点3,6和11,各个“起点”-“终点”之间各条运输线路分别如图6所示。同时,分流设施对于相连路段的关闭情况分别如图6所示。但是,需要注意的是,对于不同的运输线路,各分流设施关闭和开放的路段会有所不同。还有,经过设立3个分流设施之后,各个“起点”-“终点”之间有害物品运输的风险与行驶距离分别如表5所示。
1-19 车辆行驶路径对比图 1-20车辆行驶路径对比图 2-19 车辆行驶路径对比 2-20 车辆行驶路径对比

设有分流设施的节点原行车路径控制后行车路径分流设施选择关闭的路段 图6 设3个分流点的情况下有害物品车辆行车路径示意图
1-19 车辆行驶路径对比图 1-20 车辆行驶路径对比图 2-19 车辆行驶路径对比图 2-20 车辆行驶路径对比图

设有分流设施的节点原行车路径控制后行车路径分流设施选择关闭的路段图7设5个分流点的情况下有害物品车辆行车路径示意图

表5 设置3个分流设施方案及计算结果
5.2.4 设置5个分流设施的方案
在设置5个分流设施的成本约束下,根据给出的模型,可以得到分流设施位置在节点4, 6, 9, 14和17,各个“起点”-“终点”之间各条运输线路分别如图7所示。同时,分流设施对于相连路段的关闭情况分别如图7所示。但是,需要注意的是,对于不同的运输线路,各分流设施关闭和开放的路段会有所不同。还有,各个“起点”-“终点”之间有害物品运输的风险与行驶距离分别如表6所示。
5.2.5 设置20个分流设施的方案
特别地,在没有成本约束的条件下,即所有节点均设置分流设施,总风险应该达到理论上的最小值;根据给出的模型,可以得到各个“起点”-“终点”之间各条运输线路分别如图8所示,各个“起点”-“终点”之间有害物品运输 的风险与行驶距离分别如表7所示。
显然,此时各个起点-终点之间有害物品运输路径为最小风险路径,将所有其他的路段全部关闭。当然,不同起点-终点之前所关闭的路段会有所不同。
表7所有节点设置分流设施的方案的计算结果
1-19 车辆行驶路径对比图 1-20 车辆行驶路径对比图 2-19 车辆行驶路径对比图 2-20 车辆行驶路径对比图

设有分流设施的节点原行车路径控制后行车路径分流设施选择关闭的路段图8设20个分流点的情况下有害物品车辆行车路径示意图
5.3 各方案比较
根据给出的模型,可以得到分流设施数量从0~20之间,给定设施数量下的最优分流设施位置,相应的风险以及行车成本,具体结果如表8所示。特别地,当分流设施的数量超过5个,其最优策略不再改变。因此,表8中略去了设施为6~19之间最优设施的策略与相应数值。
表8 各设点方案的结果比较

设施数量设置的节点总路径距离增加比例总风险风险减少比例 0-23870000-96.577- 122712600013%53.06845% 26,142827700018%43.53855% 33,6,113013600026%23.71475% 41,9,14,163241100035%22.72876% 54,6,9,14,173784900058%19.91079% 6-19-3784900058%19.91079% 201,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,203784900058%19.91079%
特别地,通过比较总风险和总路程相对原方案变化的比例可知:相对于总路程的增加比例,总风险降低的比例更加显著,如图10所示。相对于原方案(不设置分流设施),设立1个分流设施的方案使得总路程增加不到13%,而总风险下降了45%;设立2个分流设施的方案使得总路程增加18%,总风险却降低了55%;而设立3个分流设施的方案使得总路程增加26%,总风险却降低了75%。
由此可见,仅仅少量的分流设施的设定,尽管带来较少总路程上升,但是可以非常有效地降低有害物品运输给区域人口带来的风险。因此,对于政府而言,通过设立较少的分流设施就以有效降低有害物品运输风险,值得政府部门进行和推广这样的工作。
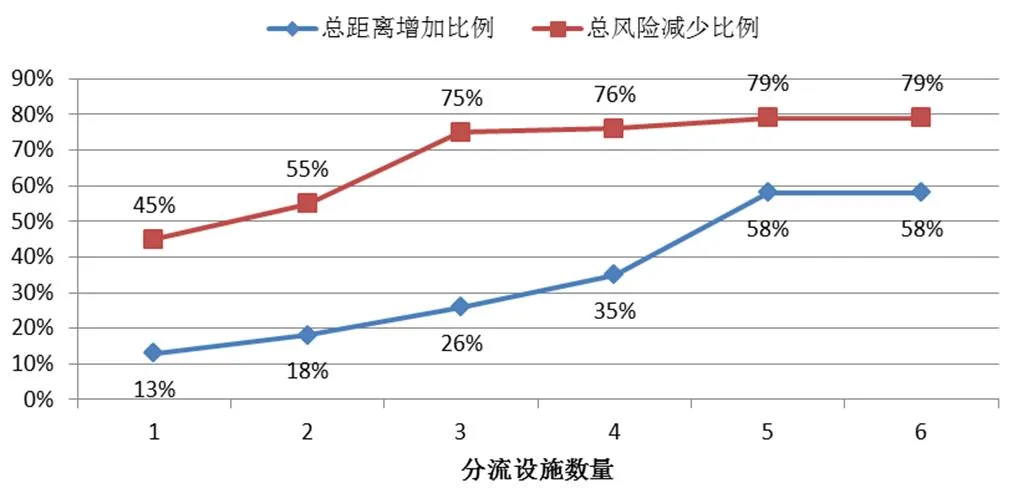
图10 设点方案与原方案相比的风险与距离改变情况
6 结论
现实生活中,运输有害物品的承运商为了追求成本的最小化,一般以成本最小的最短路来选择路径行驶车辆;而另一方面,由于有害物品的危害性,政府希望降低有害物品运输对公众和环境的影响,可以通过设立分流设施,对途经有害物品运输的车辆进行分流控制,即对于不同车辆关闭特定的路段,限制和改变运输有害物品车辆的原有行车路径, 使其避开事故高发路段和人口密集区域,达到降低风险的效果。
对以风险最小化为目标的有害物品运输网络中分流设施选址以及车辆分流问题进行了研究。首先,对有害物品运输中的分流控制问题进行了描述,建立了以总风险最小化为目标的有害物品运输车辆分流控制双层模型,模型的首层为分流设施的选址问题,第二层为每辆有害物品运输车辆关闭路段的选择问题。然后,利用KKT条件将双层模型转化为单层混合整数规划,并将非线性约束转化为线性约束。最后,以华北-华东地区的运输图为例,说明了分流设施的总风险最小化模型在实际中的应用,算例表明分流设施的设置能够非常有效地降低有害物品运输带来的风险。
[1] List G, et al. Modeling and analysis for hazardous materials transportation: risk analysis, routing scheduling and facility location [J]. Transportation Science, 1991, 25(2): 100-114.
[2] 魏国, 杨志峰, 李玉红. 城市危险化学品事故统计分析与对策[J]. 环境污染与防治, 2006, 28(9):711-714.
[3] 吴宗之,孙猛. 200起危险化学品公路运输事故的统计分析及对策研究[J]. 中国安全生产科学技术, 2006, 2(2): 3-8.
[4] 魏国, 杨志峰, 李玉红.非爆炸品类危险化学品事故统计分析及对策[J]. 北京师范大学学报(自然科学版), 2005, 41(2): 209-212.
[5] Verter V, Kara B. A path-based approach for hazmat transport network design[J]. Management Science, 2008, 54(1): 29-40.
[6] Erkut E, Gzara F. Solving the hazmat transport network design problem[J]. Computers & Operations Research, 2008, 35: 2234-2247.
[7] Erkut E, Alp O. Integrated Routing and Scheduling of Hazmat Trucks with Stops En Route[J]. Transportation Science, 2007, 41(1):107-122.
[8] Nozick L, List G, Turnquist M. Integrated routing and scheduling in hazardous materials transportation[J]. Transportation Science, 1997, 3: 200-215.
[9] George F. Routing and Emergency-response-team sitting for high-level radioactive waste shipments[J]. IEEE Transactions on Engineering Management, 1998, 45(2): 141-152.
[10] Nozick L, Turnquist M. Inventory, transportation, service quality and the location of distribution centers[J]. European Journal of Operational Research, 2001, 129(2): 362-371.
[11] Fabiano B, et al. A framework for risk assessment and decision-making strategies in dangerous good transportation[J]. Journal of Hazardous Materials, 2002, 93: 1-15.
[12] 张江华,刘治平,朱道立. 多源点突发灾害事故应急疏散模型与算法[J]. 管理科学学报, 2009, 12(3): 111-118.
[13] 魏航. 时变条件下有害物品运输的路径选择研究 [D]. 成都: 西南交通大学博士论文, 2006.
[14] 魏航. 时变随机网络下有时间窗的有害物品运输路径选择研究[J]. 中国管理科学, 2009, 17(3):93-100.
[15] 张敏, 等. 危险品集成物流管理系统选址—选线模型研究[J]. 管理科学学报, 2008, 11(1): 59-67.
[16] Kara B, Verter V. Designing a Road Network for hazardous materials transportation[J]. Transportation Science, 2004, 38(2): 188-196.
[17] Marcotte P, et al. Toll Policies for Mitigating Hazardous Materials Transport Risk[J]. Transportation Science, 2009, 43(2): 228-243.
[18] Daskin S. Network and Discrete Location: Models, Algorithms and Applications[M]. New York: John Wiley, 1995. 1-121.
[19] Drezner Z, Hamacher W. Facility Location: Applications and Theory[M]. Berlin: Springer-Verlag, 2001. 1-38.
[20] ReVelle S, Eiselt A. Location analysis: A synthesis and survey[J]. European Journal of Operational Research, 2005, 165:1-19.
[21] 王刊良,徐寅峰.有害危险品运输网络中的分流点选址问题[J]. 管理工程学报, 1999, S1:21-25.
[22] Merchant D, Nemhahuser G. A Model and An algorithm for the Dynamic Traffic Assignment Problmes[J]. Transportaion Science, 12: 183-199.
[23] Merchant D, Nemhahuser G. Optimality Conditions for a Dynamic Traffic Assignment Model[J]. Transportaion Science, 12: 200-207.
[24] Yang H, Zhou J. Optimal Traffic Counting Locations for origin-destination matrix estimation[J]. Transportation research Part B: Methodological, 1998, 32(2): 109-126.
[25] Peeta S, Ziliaskopoulos A. Foundations of Dynamic Traffic Assignment: The Past, the Present and the Future[J]. Networks and Spatial Economics, 2001, 1(3-4): 233-265.
[26] Garey M, Johnson D. Computers and Intractability: A Guide to the Theory of NP-Completeness[M]. New York : W. H. Freeman and Co., 1979. 36-138.
[27] Bard J. Practical Bilevel Optimization: Algorithms and Applications[M]. Amsterdam: Kluwer Academic Publishers, 1998. 65-98.
[28] Wolsey L. Integer Programming[M]. New York: John Wiley and Sons, 1998. 89-156.
Network Design for Route Control of Hazardous Materials Transportation
WEI Hang, ZHONG Zhi-long, CHEN Jing
(International Management for Business School, Shanghai University of Finance & Economics, Shanghai 200433, China)
As China is developing its economy, hazardous materials have been increasingly produced and transported. These materials pose potential risks to the environment and people. People have great concerns in areas where hazardous materials are produced, transported, stored, and used. In the process of transporting hazardous materials, transporters often pass through areas with dense population, and cause potential risks to them. This paper developed an approach to address this special problem. By using the traffic assignment facility, government can reduce risks by controlling the routes of vehicles that carry hazardous materials in order to avoid populated areas. This paper wants to optimally select the locations of assignment facility and assign vehicles to the right path with the objective of achieving the lowest risk.
The introduction section reviewed literatures related to the transportation of hazardous materials in four aspects: route choosing, transportation network design, facility locating in discrete network, and traffic assigning. The current literature lacks of study about reducing risks by the means of traffic assignment facilities. To narrow the research gap, this paper adopts “multi-origin and multi-destination” approaches to study the transportation of hazardous materials. These approaches emphasize on the locations of facilities on one hand and the selections of links for shut down on the other hand.
The analysis section discusses the mechanism of overall assignment systems. In general, government aims to minimize the total risk and logistics providers try to minimize the total cost. The bi-level mechanism is evident because government decides the locations and function of traffic assignment facilities. In contrast, distributors try to minimize the cost of routes according to government policy.
Based on the analysis, a general math description and a bi-level model are established. The upper level of the model is a non-linear integer programming, and the lower level is a constrained shortest path model. A combination of non-linear integer programming with bi-level programming results in a NP-hard model. The model is further improved with two transformations. The first transformation is to replace the lower level with a series of constraints based on the KKT condition. As a result, the bi-level model was transformed into a single model. The second transformation is to replace non-linear constraints with linear ones by introducing a big R or changing original constraints. Hence a single-level 0-1 linear model is established as the result of the two transformations.
In the section of numerical calculation, a simplified network is developed out of east- and- north China’s road networks, and the numerical outcomes of traffic assignment facilities in number from 1 to 20 are respectively given and further compared with each other. The results show that the larger the number of facilities the greater the reduction of the total risk and the increase of the total transportation distance. In addition, when the number of facilities is 5, the total risk and transportation distance do not change even if the number of facilities continues to increase. In conclusion, even relatively small number of traffic assignment facilities would significantly reduce the total risk of hazardous materials transportation in spite of increase in total distance.
hazardous materials transportation; network design; risk; route control
中文编辑:杜 健;英文编辑:Charlie C. Chen
U116.2
A
1004-6062(2016)02-0233-10
10.13587/j.cnki.jieem.2016.02.029
2012-06-24
2014-01-03
国家自然科学基金资助项目(71272016);浙江省自然基金资助项目(LY12G02003)
魏航(1976-),男,浙江绍兴人。上海财经大学国际工商管理学院副教授,博士,研究方向:运输管理,应急管理。
① 由于其他与分流设施不相连的路段分流设施是无法影响其路线选择,因为也无法进行分流控制。因此,在此假设分流设施能够进行分流控制的路段为与分流设施相连的路段,即能够选择关闭的路径必定包含分流设施。
② 特别地,若是只有单起点-单终点的情况,其需要将除了最小风险路径之外的所有路段进行关闭。显然,这种方式不是很符合实际情况。

