曲率半径对小半径曲线梁桥的内力影响研究
代征军
(安徽省交通规划设计研究总院股份有限公司,安徽 合肥 230088)
曲率半径对小半径曲线梁桥的内力影响研究
代征军
(安徽省交通规划设计研究总院股份有限公司,安徽 合肥 230088)
为了研究曲率半径对曲线梁桥结构受力的影响,文章以某预应力混凝土曲线梁桥作为研究对象,采用有限元计算法,通过设置三种不同曲率半径的弯桥方案,分别分析结构在恒载、活载及组合作用下的受力规律,找出最不利的影响因素,提出相应的解决方案,为曲线梁桥结构的设计提供一定的参考。
曲率半径;预应力混凝土;曲线梁桥;有限元
0 引 言
由于曲线梁桥的适应性较强,能够满足各种弯曲路线总体的需求,该桥型在城市道路及高速公路建设中得到越来越广泛的应用[1-3]。研究表明,曲线梁桥在曲率半径的影响下,会产生较为明显的弯扭耦合作用[1-10],从而导致该桥型出现各种不利的结构病害。
曲率半径是曲线梁桥受力的最主要的控制因素之一[1,6-7],随着曲率半径的增大,结构出现的不利作用越来越明显,为了详细研究曲率半径在结构受力中的影响,本文以某五跨预应力混凝土连续梁桥作为研究对象,设置三种不同的曲梁半径方案,以单纯扭转理论[1,6,9-10]为基础,建立空间梁元[5,7]模型,分别计算恒载、活载及组合作用下的结构扭转效应及变形大小,从而找出不同曲率半径下的最不利受力影响因子,提出一定的解决方案,为曲线梁桥设计提供指导。
1 工程概况及研究方案
本文以某一互通匝道桥的第一联为研究对象,该联为预应力混凝土现浇箱梁结构,跨径布置为5×25 m,梁高为1.5 m,单箱双室结构,桥梁的跨中横断面如图1所示。
为了有效反映曲率半径对结构受力的影响,对该桥梁拟定了三种曲梁半径,即:方案一:R=180 m;方案二:R=120 m;方案三:R=90 m。
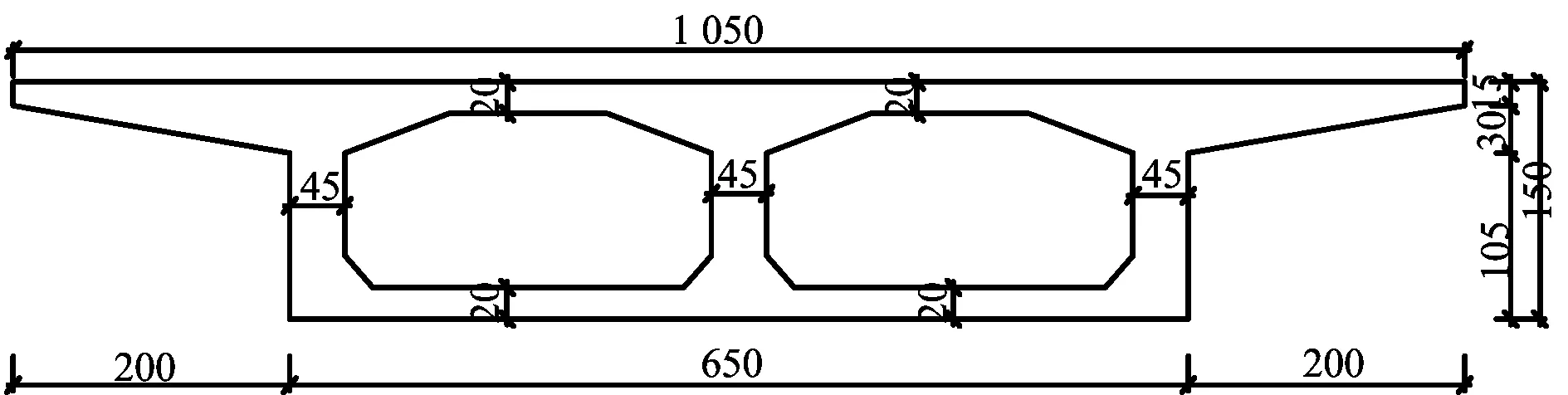
图1 曲线梁桥跨中横断面
2 计算结果
研究表明,在采用单纯扭转理论中的平截面假定[1,6,8]时,曲率变化对结构的竖向弯矩影响不大,因此,本次计算重点研究各种工况下不同半径的曲梁结构扭转作用、横向弯矩效应及支座反力变化规律,找出各种效应的最不利影响因子,提出一定的解决措施。
2.1 扭矩计算结果
三种半径的曲梁结构在恒载、活载、预应力及基本组合作用等工况下的扭矩计算结果如图2所示。
由图2可看出,在活载作用下,曲梁结构的曲率半径变化对结构所受的扭矩大小影响很小,其值基本不变;在恒载、预应力荷载及组合作用下,曲梁结构所受到的扭转作用随曲率半径的增加而增大;在组合作用下,曲梁结构的梁端及支点处受到的扭转作用最大。由以上可知,在设计时应注重曲梁端部及支点的设计,可采取加大横梁尺寸等措施来减少结构端部及支点的扭转作用。
2.2 扭转变形计算结果
三种半径的曲梁结构在不同荷载工况下的最不利扭转位移计算结果如图3所示。
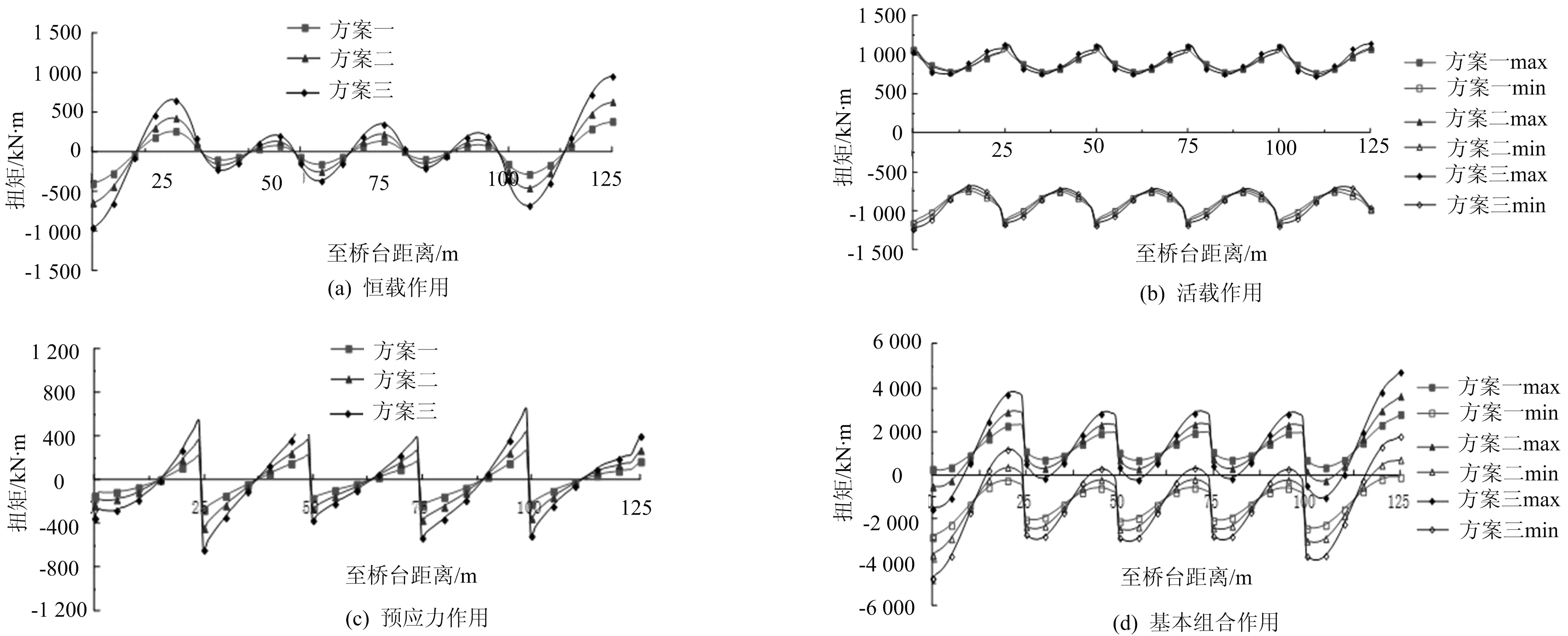
图2 不同曲率半径下的曲梁结构扭转图

图3 不同曲率半径下的曲梁结构横向弯矩图
由图3可以看出,几种曲率半径条件下,各主梁的扭转变形作用随着曲率半径的增大而增加,主梁结构在不同荷载工况作用下,边跨的扭转变形最大,因此设计中要着重考虑到曲梁结构边跨的扭转效应。
2.3 横向弯矩计算结果
本次研究仅对三种方案在各种荷载工况下的结构横向弯矩进行计算,其计算结果如图4所示。

图4 不同曲率半径下的曲梁结构横向弯矩图
由图4可看出,曲梁结构在几种荷载工况下的横向弯矩随着曲率半径的增加而逐渐变大,通过对比图4(a)、图4(b)、图4(c)可发现,预应力荷载对曲梁结构的横向受弯影响最大,活载与恒载影响相对较小,但变化趋势均相同。由此可知,预应力荷载在主梁的横向蠕变中起到关键作用,在对结构进行设计时需要着重考虑该因素的不利作用,必要时可减小跨径,取消预应力,采用普通钢筋混凝土曲梁结构。
2.4 支承反力计算结果
本次研究仅分析三种方案在基本组合作用下的支承反力变化规律,其计算结果如表1所列。

表1 不同曲率半径下的结构支承反力计算 kN
由表1可知,随着曲率半径的增加,曲梁结构各个墩台的支座反力均出现内侧变小、外侧变大的趋势,且变化趋势较为明显,由此可知,在曲率半径达到一定极限值时,结构内侧支座反力有可能出现负值,最终导致结构向外侧翻。为避免结构产生侧翻,设计时需根据实际计算结果设置一定规格的抗拉支座。
3 结 论
(1) 随着曲率半径的增加,曲梁结构的扭转效应逐渐增大,其中,梁端及支点的扭转效应相对于其他部位更为不利,在设计时,可采取加大横梁尺寸等措施来减少结构端部及支点的扭转作用。
(2) 曲梁结构的预应力荷载是导致梁体横向蠕变中起到关键作用的因素,设计时需要着重考虑该因素的不利影响,必要时可采取减小跨径,将梁体设计为普通钢筋混凝土结构。
(3) 随着曲率半径的增加,支座反力呈现内侧减小、外侧增大的趋势,当达到一定程度时,会导致结构产生侧翻,为避免该类问题的出现,设计时需根据实际计算情况设置一定规格的抗拉支座。
[1] 姚玲森.曲线梁[M].北京:人民交通出版社,1989.
[2] 刘云飞.曲线梁桥的设计理论与工程应用[D].天津:天津大学,2004.
[3] 方诗圣,肖 兵,张吉烁,等.支座布置形式对曲线梁桥力学性能的影响[J].世界桥梁, 2011(4):49~52.
[4] 邵容光,夏 淦.混凝土弯梁桥[M].北京:人民交通出版社, 1996.
[5] 陈华有.城市桥梁中小半径曲线梁桥设计分析[J].中国水运(理论版),2008(1):147~148.
[6] 孙广华.曲线梁桥计算[M].北京:人民交通出版社,1997.
[7] 朱 琳.预应力混凝土曲线梁桥抗扭设计分析[D].武汉:武汉理工大学,2006.
[8] 李国豪.桥梁与结构理论研究[M].上海:上海科学技术文献出版社,1983.
[9] 李明昭.断面可变形的矩形箱式薄壁圆弧曲杆静力分析法[J].同济大学学报,1982(2):39~42.
[10] 高岛春生.曲线梁桥[M].张德礼译. 北京:中国建筑工业出版社,1979.
2016-10-10;修改日期:2016-10-12
代征军(1975-),男,安徽含山人,安徽省交通规划设计研究总院股份有限公司高级工程师.
U448.42
A
1673-5781(2016)05-0589-03

