基于Copula的东江流域丰枯遭遇及洪水频率分析*
张正浩,张 强,史培军
(1.中山大学水资源与环境系∥华南地区水循环与水安全广东省普通高校重点实验室∥广东省城市化与地理环境空间模拟重点实验室,广东 广州510275;2.北京师范大学环境演变与自然灾害教育部重点实验室∥地表过程与资源生态国家重点实验室∥减灾与应急管理研究院,北京100875)
基于Copula的东江流域丰枯遭遇及洪水频率分析*
张正浩1,张 强2,史培军2
(1.中山大学水资源与环境系∥华南地区水循环与水安全广东省普通高校重点实验室∥广东省城市化与地理环境空间模拟重点实验室,广东 广州510275;2.北京师范大学环境演变与自然灾害教育部重点实验室∥地表过程与资源生态国家重点实验室∥减灾与应急管理研究院,北京100875)
利用Copula函数分析了东江流域径流量边缘分布,分析各水文站点洪水频率,得出水库建成前后流域上中下游丰枯遭遇变化。研究表明:① 广义极值分布与对数分布为东江流域洪水过程研究的最优分布。Gumbel Hougaard Copula函数对所有站点丰枯组合拟合效果较优;② 三大水库对6组丰枯组合遭遇的影响有显著差异性:下游水库削峰填谷作用对丰枯组合影响明显,博罗-岭下组合平平遭遇概率增大最多,为4%;中上游水库削峰填谷作用对丰枯组合遭遇影响不明显,但其平平遭遇概率均有增大趋势,东江流域径流整体趋于平坦化;③ 龙川、河源、岭下、博罗4个水文站点水文过程皆受水利工程影响,洪峰流量与洪水总量在1974年后不再同时出现最大值,有效减小了洪灾威胁;④ 水库建成后不仅能通过削峰填枯作用降低洪峰流量与洪水总量,更能提高其联合重现期与同现重现期,减少洪水极大值分别或同时出现的概率,对流域的防洪有利。
边缘分布;Copula函数;丰枯遭遇;重现期
流域地表水文过程受气候变化与人类活动强烈影响而发生显著变异[1]。其中,洪水对社会经济发展和人们生产生活安全有重要威胁[2]。随着经济发展、人口增长及不合理的土地利用,洪水产生的经济损失逐年增大[3]。丰枯遭遇的研究对了解流域间同时发生丰或枯水的可能性、进一步认识水资源的区域再分配过程[4]以及城市联合防洪等提供科学依据[5]。
东江流域地处我国亚热带,气候温和,多年平均雨量为1 750 mm,年径流量较丰沛且年内变化较大,流域70%~80%的年降雨量和年径流量集中在每年4-9月。东江流域为河源、惠州、东莞、广州、深圳以及香港3 000余万人口的水源地。香港年淡水需求量的80%通过粤港供水工程从东江获取。东江水利水电开发强度极大,目前流域内兴建了大中小型水电站700余座,包括流域3大控制性水库(新丰江水库、枫树坝水库、白盆珠水库)和干流12座梯级电站,显著影响地表水文过程。
以往的研究主要集中于使用Copula函数单独分析区域丰枯遭遇或洪水频率[4,6-8],并没有结合二者进行系统分析,而进行丰枯遭遇的研究可为城市联合防洪提供关键依据。因此,选取龙川、河源、岭下和博罗四个水文站的日径流数据,结合水利工程对站点的影响,研究两两站点的丰枯遭遇,同时根据各站点洪峰流量和7 d洪水总量建立联合重现期与同现重现期,系统研究东江流域地表水文过程及其水利工程的影响,该研究对于流域防洪、流域供水安全等具有重要科学与理论意义。
1 数 据
1954-2009年龙川、河源、岭下、博罗4个水文站的实测日径流量数据,数据完整性好,无缺测值(图1)。20世纪50-60年代初,东江流域内综合治理及人类活动影响很少,近似于天然状态,虽然新丰江水库于1962年竣工,水库对东江流域上中下游的影响并不大,径流受水库影响较少[9]。通过前人的研究,使用Mann-Kendall 趋势检验、水文变异系统分析、小波分析、扫描式t检验法等方法,得出龙川、河源、岭下和博罗变异时间为1973年[10-11]。综上所述,本文选取东江流域的变异点为1973年。选取1954-1973年为水库建成前时期,1974-2009年为水库建成后时期。
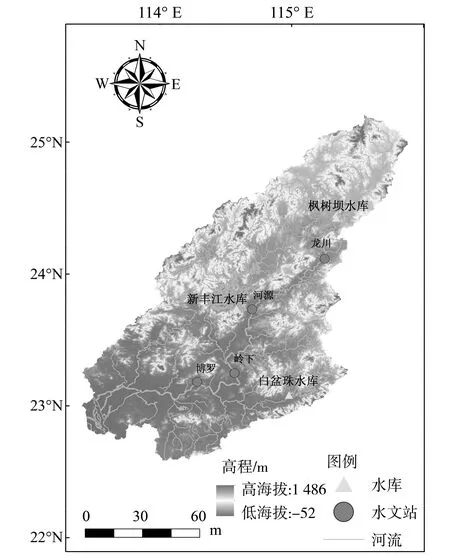
图1 东江流域水系图Fig.1 The locations of the hydrological and precipitation stations within the East River basin
2 研究方法
2.1 边缘分布选择和参数估计
水文频率计算的2个基本问题是分布线型选择和参数的估计[12]。本文使用对数皮尔逊三型、广义极值分布(GEV)[13]、对数正态分布(LOGN)等10种分布对水文变量进行边缘分布拟合,并采用Kolmogorov Smirnov(K-S)检验、Anderson Darling(A-D)检验对拟合优度进行综合检验。
2.2 二维Copula联合分布函数和非参数估计
本文采用此类型二维Copula函数中的Gumbel-Hougaard、Clayton和Frank Copula函数构建径流联合分布函数,通过Genest和Rivest提出的非参数估计方法计算3种Copula函数[14],再根据OLS方法选取最优Copula函数进行东江流域水文站间丰枯遭遇分析和洪水频率分析。
2.3 丰枯遭遇情况划分
丰枯指标分为丰、平、枯3级,取丰、枯水划分的累积概率分别为pf=62.5%和pk=37.5%[4],通过最优二维Copula模型可对水库与水库丰枯的遭遇性进行研究,2个水库的丰枯遭遇可以分为丰丰、丰平、丰枯、平丰、平平、平枯、枯丰、枯平、枯枯共9种情况[4]。
2.4 两变量联合概率分布
通常联合事件(x,y)的联合概率分布记为F,表达式如下:
(1)
联合重现期是指变量中至少有一个超过某一特定值时事件发生的重现期,计算公式为:
(2)
同现重现期是指2个变量同时超过特定值时事件发生的重现期,其公式为:
(3)
2.5 离差平方和最小准则[15]
离差平方和最小准和常用于评价Copula函数拟合好坏,最佳的Copula函数对应最小的OLS,OLS准则公式为
(4)
3 结 果
3.1 最优Copula函数模型的确定
3.1.1 边际最优分布函数的确定 以龙川水文站建库前径流序列(1954-1973年)和建库后序列(1974-2009年)为例,选用上述两种检验方法对10种分布函数进行拟合优度分析,综合检验结果表明广义极值分布为龙川站水库建成前后水文序列最优概率分布函数(表1),由于篇幅所限,省略了河源、岭下以及博罗的概率分布函数拟合优度检验表,采用相同方法对其它各水文站日流量序列进行拟合优度检验分析,求出建库前河源、岭下和博罗的最优分布函数皆为广义极值分布,水库建成后河源、岭下和博罗的最优分布分别为广义极值分布、对数分布和对数分布。对于下文选择洪峰流量与洪水总量的最优分布,其结果相似,在此不再详述。
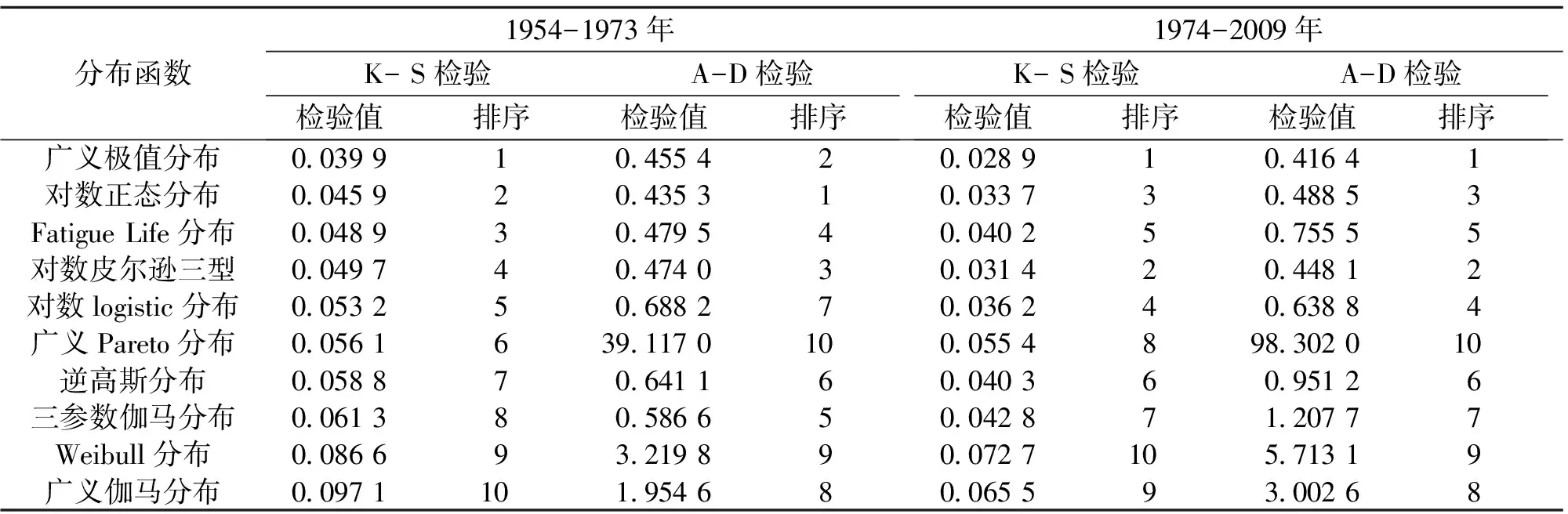
表1 龙川年径流量的10种概率分布函数拟合优度检验表
3.1.2 最优Copula函数的确定 本文采用离差平方和最小准则(OLS)评价Copula方法的有效性,并选取OLS最小的Copula为最优Copula。
从表2看出,无论水库建成前(1954-1973年)或建成后(1974-2009年),GumbelHougaardCopula函数在东江流域水文站与水文站间具有基本通用性,且对所有站点组合拟合效果较优。对于下文选择洪峰流量与洪水总量的最优Copula函数,其结果相似,在此不再详述。

表2 二维Copula联合分布函数OLS评价结果
3.2 丰枯遭遇趋势分析
从图2-4看出,龙川、河源、岭下和博罗4个水文站丰枯同步的概率在水库建成前从68%到88%,水库建成后从73%到88%,而水库建成后(1974-2009年)的平平遭遇概率均高于建成前(1954-1973年),主要是由于水库的削峰填谷的水文调节作用[16]。另外,丰丰遭遇概率除龙川-河源,龙川-岭下外,其余各组丰枯遭遇概率均下降,河源与岭下虽受水利工程影响,但由于龙川离新丰江水库与白盆珠水库距离均较远,径流变化仅受枫树坝水库调节的影响,丰丰遭遇概率变化不大。同时,除博罗-岭下水库建成后平平遭遇概率比建成前增加4%外,其余组合丰枯遭遇概率增加3%,而博罗水文站地处东江下游,受3大水库共同影响,岭下与河源水文站均受新丰江水库与白盆珠水库影响,岭下地处东江中下游,河源水文站接近新丰江水库,而新丰江水库是东江流域最大的水利工程,其影响程度较大,因此博罗-岭下组合和博罗-河源组合除平平遭遇概率增加外,丰丰遭遇概率下降5%和4%,枯枯遭遇概率下降2%和1%,水库对博罗-岭下组合削峰填谷作用大于其他组合。
综上所述,6组组合受3大水库影响程度不同,下游水文站丰枯遭遇受水库削峰填谷作用明显,而中上游丰枯遭遇受水库削峰填谷作用不明显,但其平平遭遇概率皆增加,表明水库同样作用于中上游水文站,使4个水文站点的径流过程趋于平坦化[16-18]。值得注意的是,6组水文站丰丰遭遇概率在水库建成前后皆高于29%,水文站间发生同丰可能性较大,在同丰遭遇下,容易导致水文站周边区域同时发生洪水,因此,有必要先研究两两水文站间水库建成前与建成后径流量联合分布概率,再分别考虑各个水文站水库建成前和建成后洪水频率及其重现期变化,为东江流域4个水文站点周边区域整体防洪排涝规划设计提供了科学依据与理论支持。
3.3 联合频率趋势分析
为进一步研究水库建成前后4个水文站点两两间径流联合遭遇情况,使用GumbelHougaardCopula函数建立4个水文站水库建成前和建成后的两两联合分布。以东江中上游组合(龙川-河源)与中下游组合(博罗-岭下)为例,由图5看出,相同概率情况下,建库后联合分布流量低于建库前联合分布流量,且东江中下游组合(如博罗-岭下)变化幅度大于中上游组合(龙川-河源),如1954-1973年龙川低于6 000m3/s且河源低于7 000m3/s的概率约为0.9,而1974-2009年概率为0.9时,龙川仅低于3 000m3/s,河源仅低于4 000m3/s,其下降幅度达到50%和43%;对于博罗岭下而言,1954-1973年博罗低于18 000m3/s且岭下低于10 000m3/s的概率为0.9,而1974-2009年同等概率下已经降为博罗低于8 000m3/s且岭下低于5 000m3/s,下降幅度约为56%与50%,这主要是由于龙川地处上游,新丰江水库影响不大,仅受枫树坝水库影响;博罗地处下游,同时受枫树坝水库与新丰江水库影响,径流变化幅度强于龙川[19-20]。龙川-岭下、龙川-博罗、岭下-河源、博罗-河源4个组合的联合分布分析结果类似,在此不再详述。
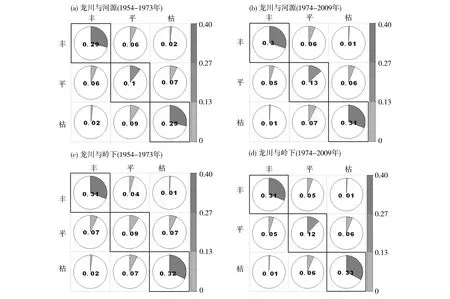
图2 水库建设前后东江流域水文站丰枯遭遇图Fig.2 The synchronous and asynchronous occurrence of high and low flow regimes before and after the construction of reservoirs

图3 水库建设前后东江流域水文站丰枯遭遇图Fig.3 The synchronous and asynchronous occurrence of high and low flow regimes before and after construction of reservoirs
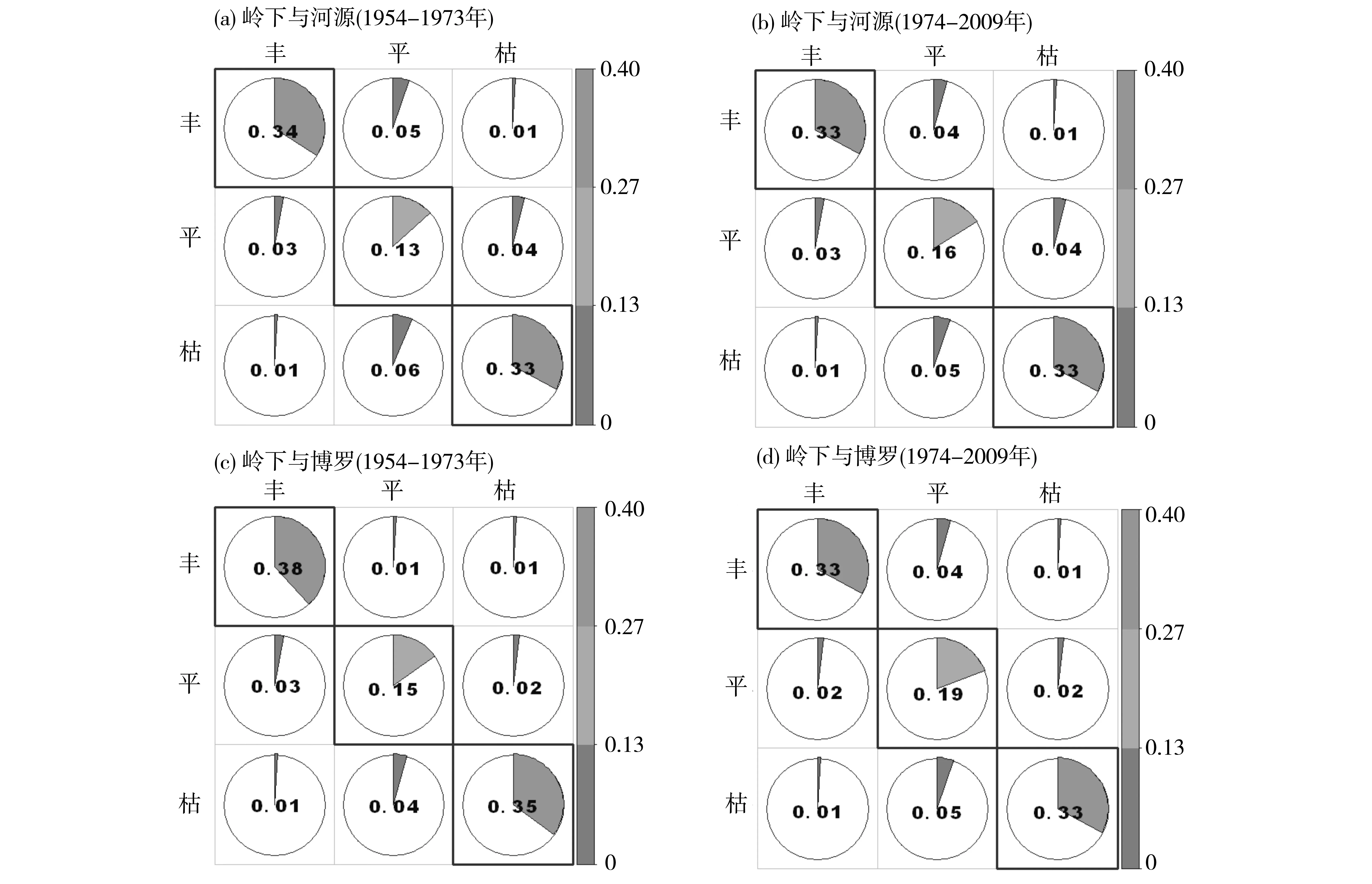
图4 水库建设前后东江流域水文站丰枯遭遇图Fig.4 The synchronous and asynchronous occurrence of high and low flows before and after the construction of reservoirs
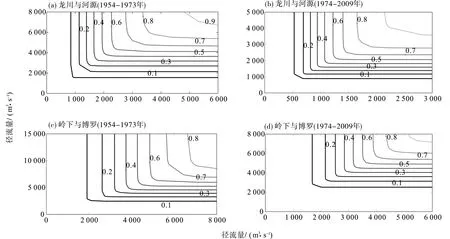
图5 水库建设前后东江流域水文站径流联合概率等值线图Fig.5 Joint probability contours of the streamflow before and after the construction of reservoirs
3.4 洪峰流量与洪水总量变异趋势分析
由图6看出,龙川、河源、岭下和博罗水库建成后洪峰流量有所降低,年际洪水总量变化幅度更小,4个水文站点洪峰流量与洪水总量最大值从上游到下游逐渐增大,其中,龙川、博罗水文站建成前洪峰流量最大值分别为6 860m3/s、18 000m3/s,年际洪水总量为16.7亿m3、65.7亿m3,水库建成后洪峰流量最大值分别为3 810m3/s、8 610m3/s,年际洪水总量为11.4亿m3和36.8亿m3,洪峰流量下降45%与52%,年际洪水总量下降32%与44%,这与前文论述水库对4个水文站点的不同影响观点吻合。

图6 水库建成前后水文站两变量洪水特征分析Fig.6 Characteristics of observed bivariate flood flows before and after construction of reservoirs
水库建成前,龙川在1964年,河源、岭下和博罗在1959年洪水总量最大,而龙川、河源在1964年,岭下和博罗在1959年洪峰流量最大,推测新丰江水库建设开始期(1958年)开始影响岭下与博罗,而新丰江水库建成后(1962年)影响龙川,河源最接近新丰江水库,因此1959年影响其洪水总量,1964年影响其洪峰流量。水库建成后,1974-2004年间,新丰江水库与枫树坝水库均已竣工,4个水文站洪峰流量与洪水总量较水库建成前趋于平坦化,1983-1984年4个水文站均发生突变,推测与白盆珠水库建设有关;2005-2009年间,由于2005年6月东江流域发生特大暴雨,致使4个水文站点2005年洪峰流量和洪水总量发生突变,2007年后恢复正常水平。
综上所述,水库建成前水文站洪峰流量和洪水总量明显高于建成后,且除河源外,其余3个水文站洪峰流量与洪水总量同时达到最大,而水库建成后仅岭下一个水文站洪峰流量与洪水总量同时达到最大,其余三者有所不同,这表明,龙川、河源、岭下、博罗4个水文站点皆受到水利工程建设的影响,洪峰流量与洪水总量在1974年后不再同时出现最大值,有效减小了灾害的威胁。
3.5 联合重现期与同现重现期
由图7可知,等高线越密集,表明径流变量增加较少重现期就增加较多,有利于防洪。整体上看,龙川受水库影响不大,水库建成前后等高线变化不明显,例如,在洪峰流量范围不变前提下,如0~2 500m3/s,水库建成前洪水流量范围从15亿m3到16亿m3联合重现期变化了20a,而1974年后从11亿m3到12亿m3变化了30a。水库作用对龙川影响较少,只起到削峰填枯作用,却没有提高联合重现期变化率。博罗水文站地处东江下游,受3大水库共同影响,水库建成前等高线稀疏,水库建成后等高线密集,洪水总量在20亿~30亿m3的范围下,水库建成前洪峰流量从10 000~15 000m3/s联合重现期仅增加了50a,而水库建成后从500~8 500m3/s即增加50a,水库不仅使博罗水文站洪水总量和洪峰流量大幅度降低,更使其洪峰流量与洪水总量的联合重现期大幅度提高,有效防止洪峰或洪量极值的发生。对于其他几个水文站联合重现期也有相似结论,在此不再详述。
由图8可知,虽然龙川水文站地处东江上游,但是由于位于东江流域上游的枫树坝水库于1973年建成后水库蓄水,导致龙川流域地表径流受到水库调节的影响[21],因此建库后洪峰流量与洪水总量的同现重现期明显大于建库前,如建库前洪峰流量大于3 000m3/s且洪水总量大于10亿m3的重现期低于20a,建库后其重现期接近100a;岭下水文站水库建成前同现重现期较小,洪峰流量大于9 000m3/s且洪水总量大于35亿m3的同现重现期仅为40a,岭下周边地区防洪压力较大;水库建成后,洪峰流量大于6 000m3/s且洪水总量高于30亿m3的同现重现期达到300a,与1954-1973年相比,不仅在水库影响下洪峰流量与洪水总量有所下降,同现重现期更是大幅度提升,推测龙川地处上游,新丰江水库影响不大,仅受枫树坝水库影响;岭下地处下游,同时受枫树坝水库与新丰江水库影响,因此同现重现期变化程度较大。这与前文论述水库对水文站点的不同影响观点吻合。

图7 东江流域水文站联合重现期等值线Fig.7 Contours of the joint return periods of peak flood volume and total flood volume
综上所述,同现重现期从龙川到博罗变化幅度逐渐增大,由于龙川地处东江流域上游,径流量较少,因此水库建库前与建库后同现重现期变化幅度不大并不影响其防洪防汛目标;岭下地处中下游,水库建成前其洪峰流量最大可达10 000m3/s以上,1954-1973年洪水总量达40亿m3以上,因此水库建成后不仅能通过削峰填枯作用降低其洪峰流量与洪水总量,更能提高其同现重现期,减少它们两者极大值同时出现时的概率,从而有利于防洪防汛的开展。对于河源、博罗水文站同现重现期有相似结论,在此不再详述。
4 结 论
1)采用KolmogorovSmirnov(K-S)检验、AndersonDarling(A-D)检验对4个水文站点径流量、洪峰流量和洪水总量分布拟合优度进行综合检验。结果显示,建库前河源、岭下和博罗的最优分布函数皆为广义极值分布,水库建成后的分布为广义极值分布、对数分布和对数分布。3种Copula函数在东江流域水文站与水文站间具有基本通用性,GumbelHougaardCopula函数对所有站点组合拟合效果较优。洪峰流量与洪水总量的最优分布及其最优Copula函数,其结果相似,在此不再详述。
2)6组组合受3大水库影响程度不同,下游水文站组合水库削峰填谷作用明显,中上游水文站组合虽然水库削峰填谷作用不明显,但是其平平遭遇概率皆有所提升,表明水库同样作用于中上游水文站,使4个水文站点的径流趋于平坦化。
3)水库建成前水文站洪峰流量和洪水总量明显高于建成后,且除河源外,其余3个水文站洪峰流量与洪水总量同时达到最大,而水库建成后仅岭下一个水文站洪峰流量与洪水总量同时达到最大,其余三者有所不同,这表明,龙川、河源、岭下、博罗4个水文站点皆受到水利工程建设的影响,洪峰流量与洪水总量在1974年后不再同时出现最大值,有效减小了灾害的威胁。
4)水库作用对龙川影响较少,只起到削峰填枯作用,却没有提高联合重现期变化率。水库不仅使博罗水文站洪水总量和洪峰流量大幅度降低,更使其洪峰流量与洪水总量的联合重现期大幅度提高,有效防止洪峰或洪量极值的发生。同现重现期从龙川到博罗变化幅度逐渐增大,由于龙川地处东江流域上游,径流量较少,因此水库建库前与建库后同现重现期变化幅度不大并不影响其防洪防汛目标;岭下地处中下游,水库建成前其洪峰流量最大可超过10 000m3/s,洪水总量达40亿m3以上,因此水库建成后不仅能通过削峰填枯作用降低其洪峰流量与洪水总量,更能提高其同现重现期,减少它们两者极大值同时出现时的概率,从而有利于防洪防汛的开展。
[1]MILLYPCD,BETANCOURTJ,FALKENMARKM,etal.Stationarityisdead:whitherwatermanagement?[J].Science, 2008,319: 573-574.
[2] KEYANYASH J A, DRACUP J A. An aggregate drought index: Assessing drought severity based on fluctuations in the hydrologic cycle and surface water storage[J]. Water Resource Research, 2004, doi: 10. 1029/2003WR002610.
[3] ZHANG Q, CHEN Y D, CHEN X, et al. Copula-based analysis of hydrological extremes and implications of hydrological behaviors in the Pearl River basin, China[J]. Journal of Hydrology, 2011, 16 (7): 598-607.
[4] 郑红星, 刘昌明. 南水北调东中两线不同水文区降水丰枯遭遇性分析[J]. 地理学报, 2000(5): 523-532.
[5] KAO S C, CHANG N B. Copula-based flood frequency analysis at Ungauged Basin confluences: Nashville, Tennessee[J]. Journal of Hydrology, 2011, 17(7): 790-799.
[6] 闫宝伟, 郭生练, 肖义. 南水北调中线水源区与受水区降水丰枯遭遇研究[J]. 水利学报, 2007,10: 1178-1185.
[7] ZHANG L, SINGH V P. Bivariate flood frequency analysis using the copula method[J]. Journal of Hydrology, 2006, 11(2): 150-164.
[8] REDDY M J, GANGULI P. Bivariate flood frequency analysis of upper Godavari River Flows using Archimedean copulas[J]. Water Resources Management, 2012, 26(14): 3995-4018.
[9] 石教智, 陈晓宏, 吴甜. 东江流域降雨径流变化趋势及其原因分析[J]. 水电能源科学, 2005, 23(5): 8-10.
[10] 涂新军, 陈晓宏, 张强. 东江径流年内分配特征及影响因素贡献分解[J]. 水科学进展, 2011, 23(4): 493-501.
[11] 张强, 崔瑛, 陈永勤. 水文变异条件下的东江流域生态径流研究[J]. 自然资源学报, 2012, 27(5): 790-800.
[12] 陈永勤, 孙鹏, 张强, 等. 基于Copula的鄱阳湖流域水文干旱频率分析[J]. 自然灾害学报, 2013(1): 75-84.
[13] 陈子燊, 刘曾美, 路剑飞. 广义极值分布参数估计方法的对比分析[J]. 中山大学学报(自然科学版), 2010, 49(6): 105-109.
[14] GENEST C, RIVEST L P. Statistical inference procedures for bivariate Archimedean Copulas[J]. American Statistical Association, 1993, 88(423): 1034-1043.
[15] 关帅, 林颖妍, 查悉妮, 等. 基于 Copula 函数的韩江流域干支流洪水遭遇分析[J]. 中山大学学报(自然科学版), 2015, 54(5): 130-137.
[16] 张强, 崔瑛, 陈晓宏, 等. 基于水利工程影响下的东江流域河流生态径流估算[J]. 珠江现代建设, 2012:1-9.
[17] ZHOU Y, ZHANG Q, LI K, et al. Hydrological effects of water reservoirs on hydrological processes in the East River (China) basin: complexity evaluations based on the multi-scale entropy analysis[J]. Hydrological Process, 2012, 26:3253-3262.
[18] ZHANG Q, JIANG T, CHEN Y D, et al. Changing properties of hydrological extremes in south China: natural variations or human influences?[J]. Hydrological Process, 2010, 24:1421-1432.
[19] CHEN Y D, YANG T, XU C Y, et al.Hydrologic alteration along the middle and upper East River (The East Riverr) basin, South China: a visually enhanced mining on the results of RVA method[J]. Stoch Environ Res Risk Assess, 2010, 24: 9-18.
[20] ZHOU Y, ZHANG Q, LI K, et al. Hydrological effects of water reservoirs on hydrological processes in the East River (China) basin: complexity evaluations based on the multi-scale entropy analysis[J]. Hydrological Process, 2012, 26:3253-3262.
[21] 谭莹莹, 谢平, 陈丽, 等. 东江流域径流序列变异分析[C]∥变化环境下的水资源响应与可持续利用.中国水利学会水资源专业委员会2009学术年会论文集, 2009: 98-104.
Copula-based flood frequency analysis with consideration of synchronous occurrence of wet/dry events in the East River basin
ZHANGZhenghao1,ZHANGQiang2,SHIPeijun2
(1.Department of Water Resources and Environment ∥Key Laboratory of Water Cycle and Water Security in Southern China of Guangdong High Education Institute∥School of Geography and Planning, Guangdong Key Laboratory for Urbanization and Geo-Simulation, Sun Yat-sen University, Guangzhou 510275, China;2. Key Laboratory of Environmental Change and Natural Disaster of Ministry of Education ∥ State Key Laboratory of Earth Surface Processes and Resource Ecology ∥Academy of Disaster Reduction and Emergency Management,Beijing Normal University, Beijing 100875, China)
As the critical water source of large cities such as Hong Kong and Guangzhou, the East River is influenced significantly in the hydrological processes by the Xinfengjiang, Fengshuba and Baipenzhu reservoirs. Copula functions are used to analyze the possibly-synchronous occurrence of high- and low- flow regimes in the East River. The results indicate that: ① The marginal distribution with the highest goodness-of-fit is log-normal distribution and generalized extreme value distribution. Meanwhile, the Gumbel Hougaard Copula has the best fitting efficacy for the inflow series of the hydrological stations; ② Three water reservoirs have great impact on the synchronous occurrence of high and low flow events at 6 pairs of hydrological stations in the downstream, the reservoirs have the filling valley and modulating peak effects which cause flattened hydrological processes when compared to those in the upper and middle East River basin. Besides, the synchronous occurrences of normalvs. normal flows in the upper and the middle East River basin show an increasing trend, causing flattened hydrological variation of the East River basin; ③ The hydrological processes at the Longchuan, Lingyuan, Lingxia and Boluo stations are heavily influenced by hydraulic facilities and scare occurrences can be observed for the peak flood flow and flood discharge, which greatly reduced the flood risks; ④ The construction of water reservoirs can flatten the hydrological processes and reduce the occurrence frequency of high and low flows, being beneficial for flood mitigation.
marginal distribution; Copula functions; synchronous occurrences; return period
10.13471/j.cnki.acta.snus.2016.06.002
2015-10-14
国家杰出青年科学基金资助项目(51425903),香港特别行政区研究资助局资助项目(CUHK441313)
张正浩(1990年生),男;研究方向:径流模拟与模型模拟分析;通讯作者:张强;E-mail: zhangq68@bnu.edu.cn
TV123;P467
A
0529-6579(2016)06-0010-10

