大口径分光计中棱镜色散光谱线弯曲的测定

李镇业，李培哲，周怡然，白在桥

(北京师范大学 物理学系，北京100875)



大口径分光计中棱镜色散光谱线弯曲的测定

李镇业，李培哲，周怡然，白在桥

(北京师范大学 物理学系，北京100875)

摘要：利用几何光学方法分析了大口径分光计光中的光谱线弯曲现象,发现不平行于棱镜主截面的光线引起了光谱线的弯曲. 如果采用与光线的倾角有关的等效折射率，不平行于主截面的光线在主截面内的投影也可以看成在按折射定律传播的光线,在此基础上得到了光谱线曲率的计算公式. 用照相法实测了光谱线的曲率，修正像差导致的误差后的测量结果与理论值符合较好.

关键词：大口径分光计；曲率；棱镜

分光计是大学物理实验传统的光学仪器，随着技术的进步与教学理念的转变，分光计的结构设计也一直在发生变化[1]. 在学习分光计的调节方法时，由于望远镜的视角很小，学生寻找“+”字反射像(或谱线)有一定的难度. 为了解决这个问题，近年来有些教学仪器厂家设计了大口径分光计. 相比普通分光计，大口径分光计视野开阔，调节和测量都比较方便. 但增大视场角也带来了问题：观察到的光谱线存在明显的弯曲. 对于这个现象，已有文献从几何光学的角度进行了分析，定性上与实验结果相符. 但由于涉及到三维空间中比较复杂的几何学，文献中并没有对谱线弯曲给出简单的物理解释和计算公式，也没有定量的测量结果[2-4]. 本文将推导谱线弯曲曲率的计算公式，并与实际测量相比较.

1现象描述与初步分析

实验使用长春禹衡时代光电科技公司生产的JJY-2型分光计(视场角为8°) 观察汞灯经过玻璃三棱镜分光后的光谱. 按要求将分光计调整完毕后，使用相机对望远镜的视野进行拍照，得到接近肉眼观察效果的照片. 使用的相机是佳能600D，镜头型号为EF-S 18-55mm f/3.5-5.6 ISII，在拍摄过程中采用手动对焦. 在所拍照片中可以发现光谱线有明显的弯曲，而且弯曲的方向为偏向角增大的方向，如图1所示.

图1　光谱线弯曲现象

为了确定导致谱线弯曲的原因，移开望远镜，用相机对三棱镜出射光线拍照(见图2)，结果发现谱线依旧弯曲，只是弯曲方向与望远镜中的图像左右相反. 去除三棱镜，将望远镜直接对准准直管时，看到的狭缝像是直线，只在视野边缘有稍许因畸变导致的弯曲. 因为整个光路分为准直管、三棱镜和望远镜3个部分，排除了望远镜和准直管的因素，可以肯定光谱线是经过三棱镜折射后产生弯曲的.

图2　三棱镜直接出射光线

2理论分析

照亮的狭缝可以认为是线光源，它位于准直管透镜的焦面上. 狭缝上给定一点发出的光经过准直管后的出射光线相互平行. 狭缝上不同点发出的光线，经过透镜后传播方向各不相同，但在同一平面内，如图3所示.

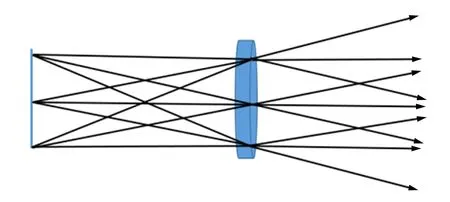
图3　准直管光路图

这些光线入射到三棱镜的前表面，如果仪器调整到位，所有入射光的方向矢量都在垂直于三棱镜主截面的一个平面内. 这些光线经过三棱镜折射后，方向矢量将不再处于同一平面内，而是发生弯曲变形，从而在望远镜的分划板上形成弯曲的光谱线. 入射光与主截面的夹角越大，光线偏离得越厉害，最终成像为谱线中越靠近边缘的部分，这与实验观察到的现象符合. 事实上，这个现象很早就被发现并讨论，不过并没有很好地解决. 文献[2]根据几何光学仔细计算了出射光线的弯曲情况，但没有得到曲率的解析表达式. 文献[3]定性分析了现象产生的原因，但没有定量计算，文献[4]计算了出射光线方向的表达式，但其形式比较复杂且不能直接与实测结果比较.

我们采用矢量分析方法分析光线在三维空间的传播. 如图4所示，光线从准直管射出，从棱镜的前表面进入棱镜，然后从棱镜的后表面射出，进入望远镜. 记棱镜前后表面的法向单位矢量分别为nf和nb,为方便起见，定义nf指向棱镜内部，nb指向棱镜外部，如图4所示.

图4　折射光路图

由几何关系有

nf·nb=cosA, nf×nb=sinAnh,

(1)

其中A为棱镜的顶角,nh为与棱镜的侧棱平行的单位矢量. nf和nb在棱镜的主截面内，nh与主截面垂直. 用光学动量表示折射定律非常方便. 光学动量定义为光线传播方向单位矢量与介质折射率的乘积. 设光线在进入棱镜之前、棱镜中和出棱镜后的光学动量分别为p1，p12和p2. 由定义有p1·p1=p2·p2=1以及p12·p12=n2，其中n为棱镜材料的折射率，而折射定律可写为[5]：

(p12-p1)×nf=(p12-p2)×nb=0,

(2)

由(p12-p1)×nf=0和nf·ph=0，可得

0=[(p12-p1)×nf]×nh=[(p12-p1)·nh]nf,

(3)

即(p12-p1)·nh=0. 同理，由(p12-p2)×nb=0和nb·nh=0可得

(p12-p2)·nh=0.

综合以上2个等式，有

p1·nh=p12·nh=p2·nh≡sinγ,

(4)

其中γ的含义是入射光线(出射光线)与棱镜主截面的夹角，γ=0对应在主截面内的光线. 任意矢量u总可以分解为垂直于主截面的分量u⊥=(u·nh)nh和平行于主截面的分量u∥=u-u⊥，(4)式说明p1⊥=p12⊥=p2⊥，所以p12∥-p1∥=p12-p1，p12∥-p2∥=p12-p2，而(2)式等价于

(p12∥-p1∥)×nf=(p12∥-p2∥)×nb=0 ,

(5)

即光线在主截面内的投影也符合折射定律，可以看成在主截面内传播的光线，它们与三维空间中真实光线唯一的区别是

p1∥·p1∥=p2∥·p2∥=1-sin2γ=cos2γ≠1,

p12∥·p12∥=n2-sin2γ≠n2,

(6)

(7)

由于棱镜折射率越大偏向角越大，而从(7)式容易知道，当γ≠0时，有ρ(γ)>n，这就是光谱线会向偏向角大的方向弯曲的原因. 为了对等效折射率的变化有数量级上的了解，考虑n=1.5情况，对于JJY-2分光计，γ最大可取到4°，ρ可增大到1.502 0. 折射率改变0.002会引起光谱线相当明显地移动，因此可以看到明显的光谱线弯曲. 而如果γ=1°，则ρ=1.500 1，改变量与折射率测量的不确定度相当，现象就不明显.

下面利用等效折射率计算光谱线弯曲的曲率. 设投影光线在棱镜前表面的入射角为θ1，在后表面的出射角为θ2，棱镜引起的光线偏转角为δ.θ2,δ都是θ1和ρ的函数，即θ2=θ2(θ1,ρ)，δ=δ(θ1,ρ)，它们由以下方程决定

(8)

实验对应的问题是固定θ1，γ改变引起ρ改变，从而引起δ的变化. (8)式求对ρ的偏导数，可得

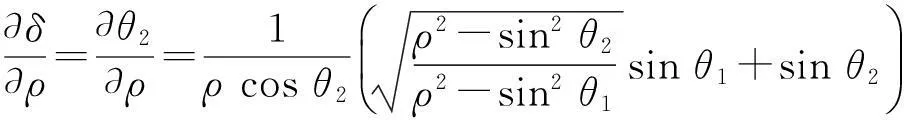
(9)

将(7)式在γ=0附近展开，可得

(10)

联合(9)式和(10)式可以得到光谱线弯曲的函数形式：

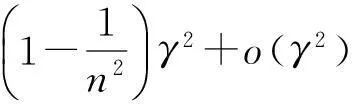
(11)

其中δ0为主截面内光线的偏向角. 当δ0为最小偏向角时，θ1=θ2=(A+δ0)/2，(11)式可简化为

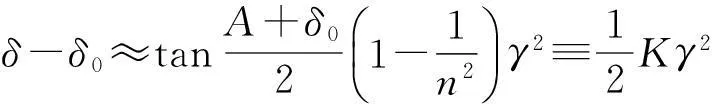
(12)

其中

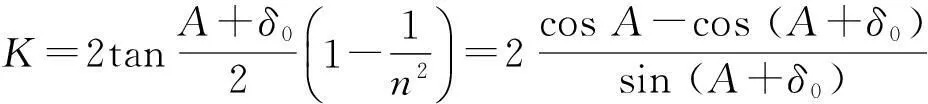
(13)

光谱线在分划板上的横纵坐标分别与tan (δ-δ0)和tanγ成比例，由于δ≈δ0,γ≈0，tanγ≈γ，(13)式就是最小偏向角时光谱线在顶点处的曲率.

3实验测定及数据处理

3.1三棱镜参量的测定

首先，按照常规实验方法测定三棱镜的参量，包括三棱镜的顶角和各条谱线的最小偏向角δ0. 然后根据公式计算出对应的n和曲率K，结果见表1,三棱镜顶角A=1.052 6 rad.

表1　三棱镜参量测定

3.2曲率实验值

以绿光光谱线为例说明曲率的测定过程：将绿色光谱线移动至最小偏向角位置，调整望远镜使其位于分划板右侧(为避免谱线被分划板挡住影响测算)尽量靠近中心的位置(减小像差)，使用相机进行对焦，得到清晰的谱线，该状态下得到的照片如图5所示.

图5　绿色谱线在最小偏向角(分划板右)

为了得到实际的曲率以便和理论公式比较，必须对照片定标，即确定相机底片像素点距离与角度变量的比例系数. 为此，保持相机位置和焦距不变，取下三棱镜，换上平面镜并转动载物台，使狭缝的反射像从左到右扫过分划板，拍下若干张照片并记录对应狭缝像的角度读数. 经过多次实验，发现照片比例尺的线性很好，因此后期实验的数据中只记录了3个位置，这已经足够保证实验的准确度. 图6是合并到同一张照片中的狭缝像.

图6　照片比例尺的确定

注意到实际狭缝反射像角度的改变量是平面镜转动的角度的2倍，从图6中读出3条光线对应的像素，结果见表2，表中平面镜角度为θ1,出射光角度为θ2.

表2　照片定标数据

将像素与出射光角度改变量进行线性拟合(已知它们具有好的线性相关性)，得到比例系数为5.194×104，即出射光角度改变1 rad，相当于在相片上移动5.194×104个像素点. 确定了照片的比例尺后，可以开始对处于最小偏向角下的绿色谱线进行处理. 处理的方式是通过Photo-shop截取绿色谱线，然后利用事先编写好的Matlab程序扫描图片亮度，将谱线所在位置点出，最后用二次函数拟合(见图7). 拟合结果为

y=1.442×10-5x2-0.034 2x+48.95,

相关系数R2=0.987. 对于二次函数，其顶点处的曲率是其二次项系数的2倍, 由此可知，实验测得的绿色谱线曲率为2.884×10-5pixel-1，由照片比例尺计算得到K绿右=1.497 rad-1，与理论值1.340 rad-1接近，但仍存在较大的偏差.

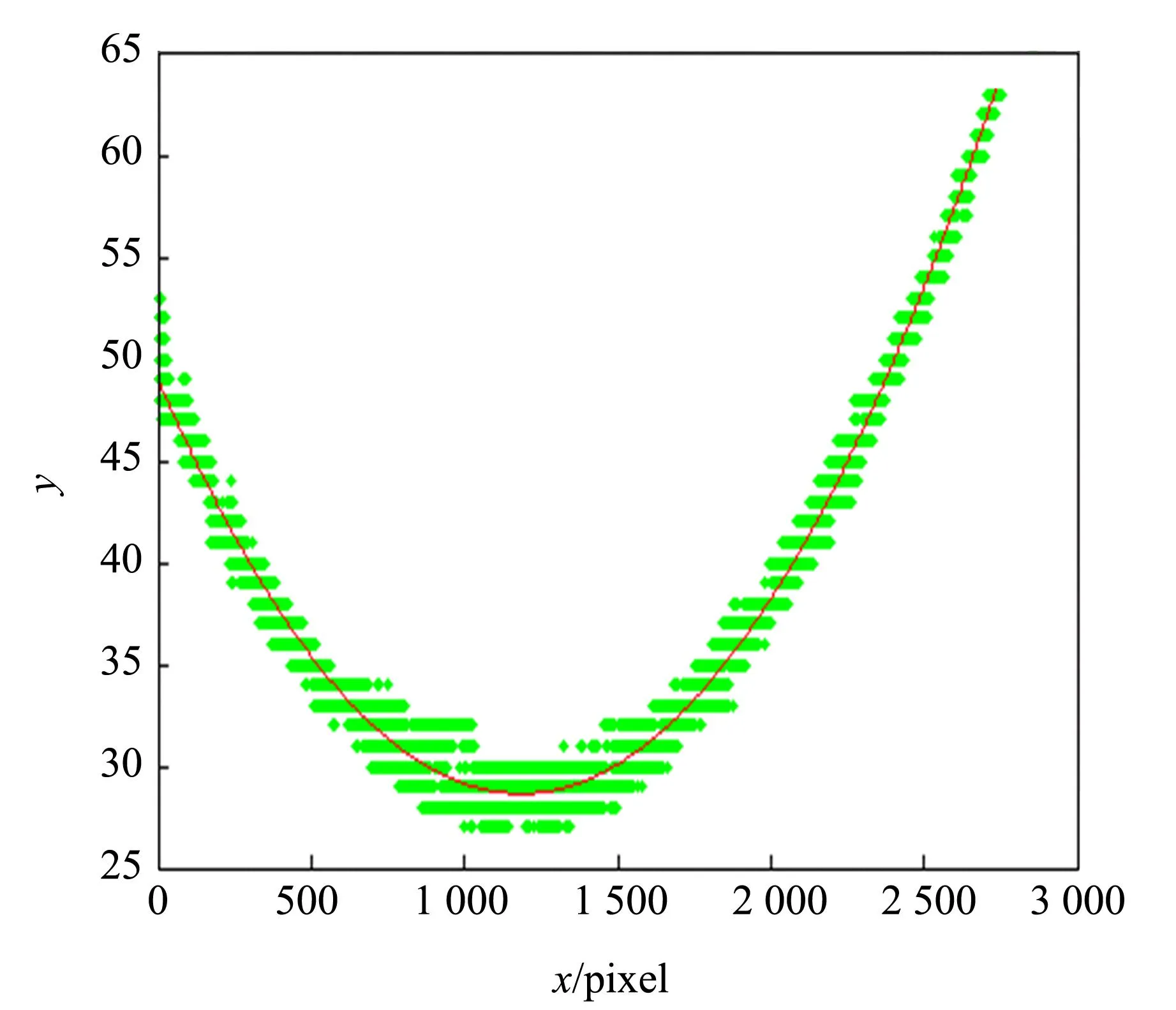
图7　谱线的二次曲线拟合

经过反复实验，考虑到调节精度，分析了产生误差的原因，最终确定望远镜产生的像差是最主要的影响因素为：为了避开分划板中下部的黑色窗口，拍到完整的谱线，照片中的谱线不可避免地偏向一边. 为消除像差造成的影响，转动望远镜，将处于最小偏向角下的绿色谱线在黑色窗口左侧靠近中央的位置成像，重复上述过程(因为望远镜移动了，相机需要移动和重新对焦，因此照片比例尺也需要重新测定，数据详见表3)，得到另一个实测绿色谱线曲率K绿左=1.202 rad-1，比理论值偏小，可见像差确实造成了很大的影响. 取2次测量值的平均值作为谱线曲率的测量值，即

与理论值的偏差仅在1%.

对于黄色和紫色谱线，同样采用上述方法得到的数据如表3所示. 由表3可见，实测值与理论值符合得很好.

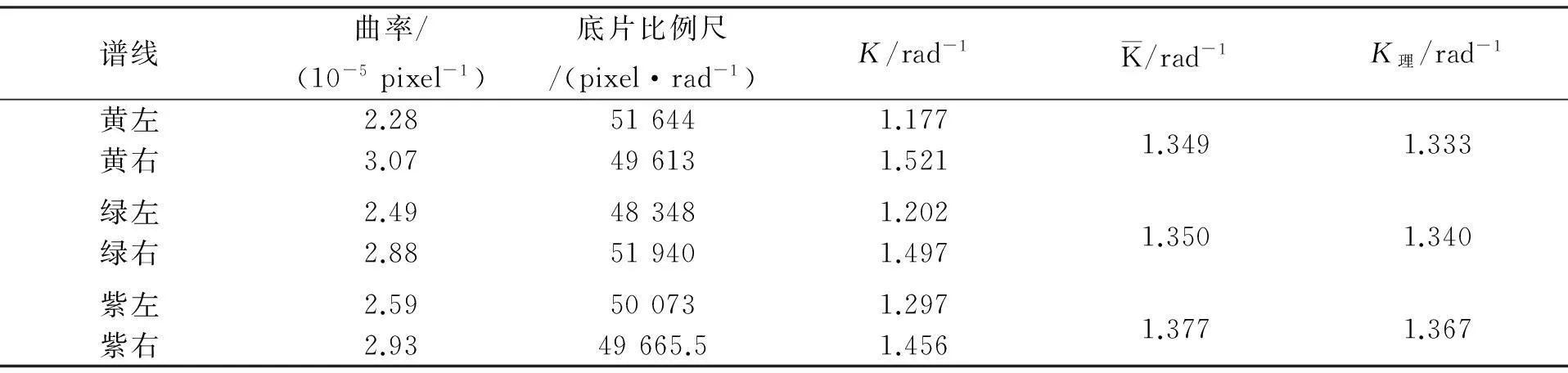
表3　实测谱线曲率与理论曲率的比较

4结论

利用几何光学原理分析了大口径分光计中光线的传播规律，定性地解释了谱线的弯曲现象，并得到了谱线顶点处曲率的计算公式. 利用照相法实测了该曲率，在修正了成像系统的像差后，所得结果与理论值符合得较好. 经分析，如果按照要求调整分光计，特别是能够保证棱镜的主截面和望远镜的光轴都与仪器的转轴垂直，准直管的狭缝方向与转轴平行，而且使用谱线的中心位置测量角度，那么谱线弯曲对实验结果的影响是可以忽略的.

参考文献：

[1]杨之昌,马世红. 漫谈教学用分光计[J]. 物理实验,2006,27(2):40-45.

[2]隋吉动,李天和. 用三棱镜测光谱时谱线弯曲的分析[J]. 黑龙江八一农垦大学学报,1986(2):97-105.

[3]卢杰,张瑛. 棱镜光谱线弯曲的分析[J]. 物理实验,1999,19(4):43.

[4]陈杰,刘国营,李文胜,等. 用分光计测量三棱镜折射率实验中的光谱弯曲现象[J]. 大学物理,2013,32(12):21-23.

[5]马科斯·玻恩,埃米尔·沃耳夫. 光学原理[M]. 7版. 杨葭荪译. 北京:电子工业出版社,2006:112.

[责任编辑：郭伟]

Measurement of the bending of spectrum lines in large aperture prism spectrometer

LI Zhen-ye, LI Pei-zhe, ZHOU Yi-ran， BAI Zai-qiao

(Department of Physics, Beijing Normal University, Beijing 100875, China)

Abstract:The bending of spectrum lines in large aperture optical spectrometer was analyzed based on geometric optics. The bending was caused by the incident rays that were not parallel to the major plane of the prism. The projection of these off-plane rays could be treated as in-plane rays if an inclination-dependent effective index of refraction was used. From this point of view, the curvature of the spectrum line was measured by the photographic method. After the error due to aberration was carefully eliminated, the measured curvature agreed with the calculated value quit well.

Key words:large aperture spectrometer; curvature; prism

中图分类号：O436.3

文献标识码：A

文章编号：1005-4642(2016)05-0029-05

作者简介：李镇业(1995-),男,山东淄博人,北京师范大学物理学系励耘实验班2013级本科生.指导教师：白在桥(1971-)，男，重庆人，北京师范大学物理学系副教授，博士，从事理论物理方面的研究工作.

收稿日期：2015-12-30；修改日期：2016-03-16