一种基于多层次方法的快速仿射谱聚类算法

苏州高等职业技术学校 李志伟



一种基于多层次方法的快速仿射谱聚类算法

苏州高等职业技术学校 李志伟

【摘要】快速放射谱聚类具有运行速度快，效率高的优点，目前受到各领域研究人员的普遍关注。本文联合使用局部距离定义、FAP算法、表征样本相似度的密度-权值矩阵构造方法，构建一种多级快速彷射谱聚类算法。最后对算法进行有效性分析，并突出本文算法的优势，为提高彷射谱聚类算法提的研究供参考。

【关键词】快速彷射谱聚类；相似度矩阵；谱聚类

1 快速仿射传播谱聚类

仿射传播聚类（AP）［1］是由 Frey 等人提出的一种新的聚类算法，其优势体现在处理类数很多的聚集时运算速度快、聚类结果有效。在人脸图像的聚类、“基因外显子”发现、搜索最优航线等方面得到了应用。该算法首先将数据集的所有样本点都视为候选的聚类中心，并为每个样本点建立与其他样本点的吸引程度的信息，即任意样本间的相似度或吸引度。然后在循环迭代过程中，各样本点竞争出最终的聚类中心。在每一轮更新的迭代过程中，若一个样本点处于其相邻样本点的中心位置，则该点与其它样本点的吸引度之和较大，在竞争中胜出的可能性也较大；反之，处在边缘位置的样本点，其吸引度之和较小而胜出的可能性也较小。这样，在竞争中胜出的聚类中心具有较大的吸引度，则属于聚类的样本点到其聚类中心的误差和比较小。因此，算法的迭代过程使得聚类的适应度函数最大化。当迭代过程收敛时，聚类中心也随之确定（即类数自动确定），再将每个样本点分配给最近的聚类中心所属的聚类，算法结束［3，4］。

从上述可知，AP算法选取了全连接图的相似矩阵用于样本的信息传播，且迭代次数较多。鉴于此，文献［2］提出了一种快速的仿射传播聚类方法（简称FAP），FAP同时考虑数据集中包含的局部和全局结构信息，是一种高特性多层图分割方法，可以应实现基于矢量和基于图的数据分割。首先，在FAP中提出了一种快速取样算法（简称FS），FS用于粗化输入的稀疏图并选择少量的具有代表性的样本作为样标，且每个样标标识一个类簇，然后基于一种定义的密度-权值的矩阵得出一种新的谱聚类方法，该方法采用全局距离对每个类簇划分成最终具有代表类簇的聚类结果，也即对类簇的合并。最后，通过样本各自对应的类标（最终的样标又称为类标）来完成所有样本点的类别划分。

由于在任何一种谱聚类算法中，相似矩阵的构造是个很重要的问题，且该矩阵构造好之后才能进行下一步的谱分解和聚类。而如文献［2］中所述，密度-权值矩阵也能够反映出样本的这种相似程度，且该矩阵的构造步骤如下：

步骤1. 定义样本点间局部长和全局距离

步骤2. 计算类簇间的距离

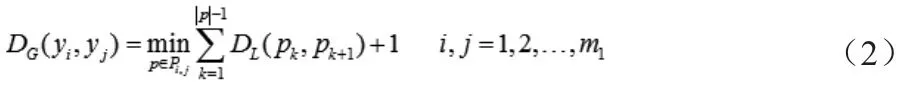
步骤3. 构造密度-权值矩阵

该矩阵被定义为：

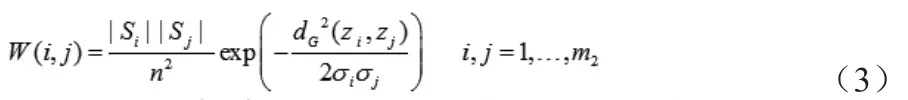
我们将由上述步骤得到的能够度量样本相似程度的密度-权值矩阵视为相似矩阵A，则基于密度-权值相似度度量的谱聚类算法实现步骤如下：

Step3.找出L的最大的K个特征向量构造V矩阵。

Step4.将V矩阵的每一行单位化，构造成Y矩阵，单元元素yij为：

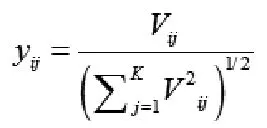
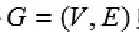
2 结束语

首先，定义出的全局距离能够相应地放大不同类样本间的距离，缩小同类样本间的距离。该距离对于噪声点和极值点具有较好的鲁棒性。能够克服文献［5］中最短路径算法中的短路问题。其次，FAP 算法不仅能够实现对稀疏图的粗化，而且能够对具有代表性标识的样本点进行提取，且在计算速度上要比AP算法快的多。这是因为AP算法选取了样本的全连接图得到的相似矩阵用于信息传播，且迭代次数较多。而FAP算法选取了有边-权值信息存在的样本构造稀疏图。这样，FAP算法不需要每次都计算所有样本的信息传播，只需要计算部分有边--权值存在的样本间的信息进行传播。另外，FAP算法在样本点间信息传播过程中能够同时考虑数据集中样本点间的局部和全局结构信息，对多层次图分割性能较高，且能够处理大规模聚类问题。

最后，将能够表征样本相似度的密度-权值矩阵视作样本的相似矩阵，得出一种基于密度-权值的谱聚类算法，该算法对标准UCI数据集、MNIST手写字和人工数据集均具有较好的聚类性能，且加速了运算速度。

参考文献

［1］Frey B， Dueck D. Clustering by passing messages between data points ［J］. Science， 2007，305（5841）﹕972-976.

［2］Shang F H，Jiao L C，Shi J R，etal.Fast affinity propagation clustering﹕A multilevel approach［J］.Pattern Recognition， 2012，45（1）﹕474-486.

［3］Kaijun Wang，Junying Zhang，Dan Li，Xinna Zhang，Tao Guo. Adaptive Affinity Propagation Clustering［J］.Acta Automatica Sinica，2007，33（12）﹕1242-1246.

［4］王开军，李健，张军英，涂重阳.半监督的仿射传播聚类［J］.计算机工程，2007，33（23）﹕197-198.

［5］Tenenbaum J， Silva V， Langford J. A global geometric framework for nonlinear dimensionality reduction［J］.Science，2000，290（5500）﹕ 2319-2323.