基于FPGA的高速高阶FIR数字滤波器的设计

胡安民 鲁少轲 邢玉鹏 李瑞 王宇

摘 要：在数字滤波器设计与应用当中，相比于以牺牲线性相位频率特性为代价的无限冲击响应（IIR）数字滤波器，有限冲击响应（FIR）数字滤波器不仅保证了精确严格的线性相位特性，并且结构简单稳定。但在实现相同的设计指标时，有限冲击响应需要更高的阶数，为满足高速高阶数字滤波器设计，文章提出一种改进的分布式算法。该算法利用主流现场可编程逻辑门阵列（FPGA）芯片的多相分解结构和流水线技术，采用多路复用加法器对数据进行预相加，减少传统分布式结构的查找表规模。利用Matalb仿真设计，Quartus II编译测试，并下载到现场可编程门阵列（FPGA）中进行运行分析，结果显示文章的方法有效地减少了滤波器对硬件资源的消耗，能够较好地实现高阶的FIR滤波器。

关键词：FIR数字滤波器；分布式算法；现场可编程门阵列；数字信号处理

数字滤波器[ 1 ]在数字信号处理中有着信号分离和信号重建的功能，是数字信号处理的重要组成部分，随着现代信号处理的高速发展，对数字滤波器的要求也越来越高，其中通过卷积实现的滤波器称为有限冲击响应（FIR）滤波器，它是一种结构简单且总是稳定的滤波器，严格意义上也只有FIR滤波器可以实现线性相位，满足了大部分线性系统的需求。

诞生于20世纪80年代的现场可编程逻辑门阵列（Field Programmable Gate Array， FPGA）和数字信号处理技术密切相关，特别是在需要大量乘累加运算的滤波器实现中有着一定的优势，分布式算法[3]（Distribute Algorithm，DA）因其充分利用了FPGA内部丰富的组合逻辑资源，能将乘积运算转换为查表操作而得到了广泛的应用。

本文对比传统的DA算法提出一种改进的分布式算法，完成高速高阶FIR数字滤波器设计，并对比给出测试结果。

1 FIR滤波器基本理论

FIR滤波器[4 - 6]，其脉冲响应由有限个采样值构成。抽头数为N，阶数为N-1的FIR系统转移函数、差分方程和单位脉冲响应如下：

由表达式可以看出乘累加运算由N次乘法运算和N-1次加法运算构成。因此常规的数字滤波器设计都是将乘累加运算分解为乘法运算和加法运算，数字滤波器的效率由硬件加法器乘法器的性能所决定，实现结构如图1所示，其中：×为硬件乘法器，+为硬件累加器，D为硬件流水线寄存器。

在使用FPGA芯片实现FIR滤波器时直接使用硬件乘法器十分耗费资源，一般是借助分布式算法利用FPGA丰富的存储资源进行查表不直接使用硬件乘法器。

2 分布式算法原理

分布式算[7- 8]（Distributed Algorithm，DA）广泛应用在数字滤波器傅里叶变换的乘累加运算之中，它的主要特点是将需要进行乘累加运算的数据进行二进制位分解，构成新的查找表（DALUT），而查找表中按地址索引存储着相应的乘积结果，用此方法完成乘累加中的乘法运算，通过移位、累加等操作得到最终的结果。分布式算法的优势在于充分利用FPGA芯片内部丰富的存储资源，如分布式的查找表内部的嵌入式RAM等，不必直接使用硬件乘法器，这对资源的折中是行之有效的。

对于线性系统乘累加结构可以简单描述为：

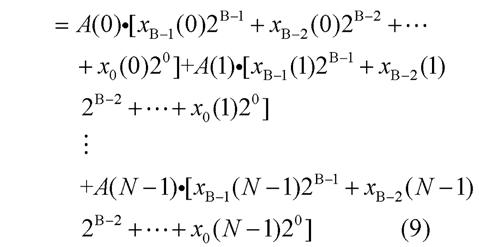
其中xb（n）表示二进制数表示的x（n）的第b位，为0或者1，为了进一步计算提取式（9）中的公因子并进行位重组：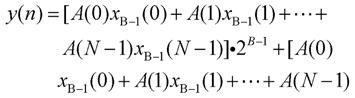

对于有输入信号为有符号数，则同理x（n），y（n）可以表示为：

传统分布式算法以速度优先实现全并行分布式FIR数字滤波器[10]，可以在一个时钟周期内实现一次滤波，硬件结构原理图如图2所示。

3 基于FPGA特性改进分布式算法

传统分布式算法的实现结构，虽然并行结构不需要通用乘法器，加快了处理速度，但查找表（DALUT）的规模深度会随着阶数的增高而变大，如实现一个32阶的数字滤波器，深度为232（4294967296），对于存储资源有限的FPGA芯片可实现的滤波器最高阶数就受到了限制。

为了提高FPGA芯片的利用率，实现高速高阶的FIR数字滤波器，本文提出如下的改进分布式算法：

将滤波器系数进行分组，利用查找表分别进行部分查表，并将结果相加，同时利用FPGA流水线寄存器，极大的减小了设计规模。

设将线性系统乘累加结构的系数分为C组则公式7可以表示如下：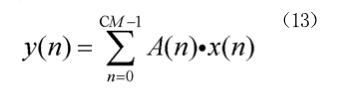

其中N=C*M。

由此将可以将一个N阶数字滤波器用C个M阶并行的查找表（DALUT）实现。因此如公式10和12可以将与y（n）表示为如下的公式（14）：

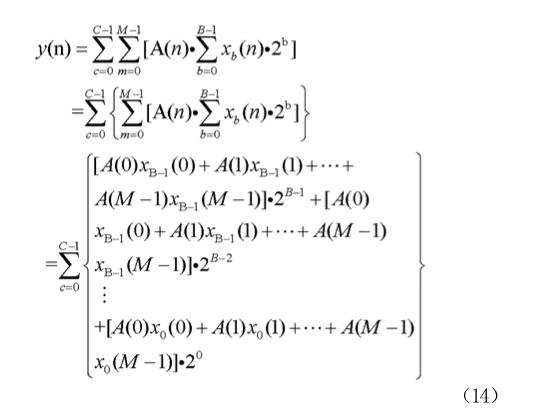
由公式（14）可知要实现C个M阶分布式乘累加结构，需要C-1个辅助加法器。

相比于传统分布式算法，假设输入信号A（0）的量化位宽为Bqua则传统分布式实现一个N阶数字滤波器查找表的大小需要（Bqua+log2N）·2N bit的RAM来存储二进制数据，并且传统的全并行分布式算法需要多个查找表，而改进的分布式算法结构对查找表的结构进行了分组优化，实现结构如图3所示，该结构与传统并行分布式算法有着的区别，为了具体说明可作如下的举例：

利用改进的分布式算法设计一个32阶数字滤波器，由32=2×16=4×8可以将32阶拆分为C=16组2阶乘累加或者C=8组4阶乘累加：C=8时，需要的查找表LUT个数8×24=128，C=16时，需要的查找表LUT个数16×22= 64。

由此可知改进的分布式算法分组越多，所需的查找表个数就越少，每个查表所占的存储资源也越少，但同时需要增加辅助加法器，在实际的工程应用中需要根据实际情况进行分组。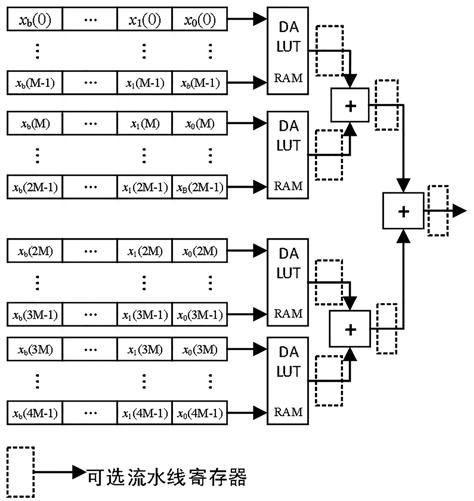

4 高速高阶FIR滤波器仿真与测试

首先借助Matlab工具箱Fdatool采用等波纹逼近法设计一个32阶低通滤波器，仿真分析后，编译VHDL语言下载到Altera公司的FPGA仿真平台（采用Cyclone IV代的EP4CE75）进一步验证本文改进的分布式算法，同时和传统分布式算法形成对比（见表1）。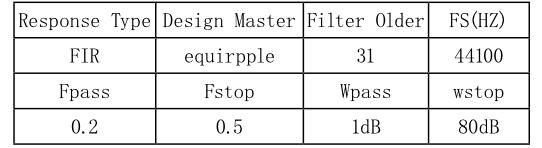

数字滤波器等波纹最佳逼近法是一种优化设计方法，它克服了窗函数法和频率采样法的缺点，使最大误差最小化并且整个逼近频段上均匀分布。用等波纹最佳逼近法设计的FIR数字滤波器的幅频响应在通带和阻带都是等波纹的如图4所示。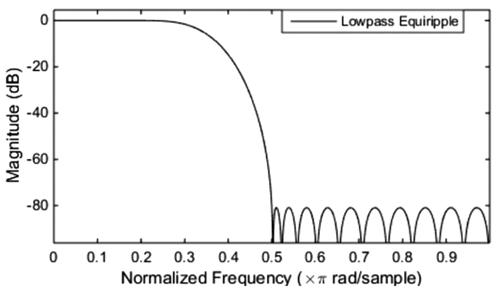

通过FDAtool获取32阶滤波器系数，并转换位定点整数，利用仿真软件Quarus II 编译VHDL程序仿真滤波器同时将MATLAB 产生的需要仿真数据量化为32bit的补码数据后下载到平台仿真测试。借助Quarus II的时序仿真工具modelsim仿真分析。其仿真结果如图5所示。从图中可以看出FPGA的运行结果与MATLAB结果相符。

同上改进VHDL语言下载到芯片实现不同的阶数，通过对Quartus II编译结果报告可以得到如表1所示的硬件资源消耗情况，本文提出的改进分布式的算法占用更少的硬件资源，在Cyclone IV EP4CE75平台下更高阶的FIR数字滤波器。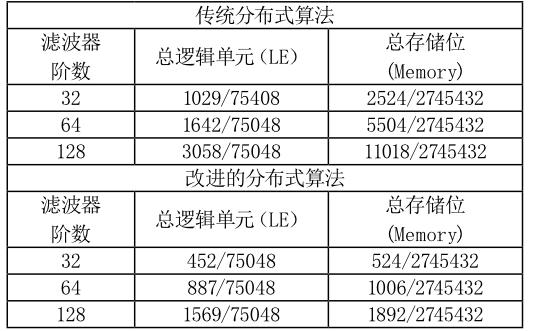

5 结论与总结

从FPGA芯片仿真运行的结果分析，本文所提出的改进的分布式算法相比传统全并行分布式算法结构更加节省内部存储器资源，在超大规模集成电路和高阶滤波器的要求下更加有效地提高硬件效率，但本文的算法只对无符号定点数的分布式算法进行了重点改进和仿真测试，对于有符号浮点数出现的更大的FPGA资源功率的消耗仍需更进一步的研究。

[参考文献]

[1]周先春，石兰芳.数字信号处理[M].北京：清华大学出版社，2015.

[2]Uwe Mary-Baese.数字信号处理的FPGA实现[M].刘凌，译.3版.北京：清华大学大学出版社，2011.

[3]曲仕茹，彭纪昌.一种在FPGA上实现的FIR滤波器的资源优化算法[J].电子设计工程，2013（14）：147-150.

[4]赵岸，颜毅华，陈林杰，等.基于FPGA高速FIR数字滤波器设计的改进方法[J].天文研究与技术，2015（1）：109-116.

[5]李泽明，李锦明，杨燕姣.基于FPGA的高阶FIR滤波器设计[J].科学技术与工程，2013（23）：6903-6906.

[6]崔亮，张芝贤.基于FPGA设计的FIR滤波器的实现与对比[J].电子设计工程，2012（20）：168-170.

[7]MEHER P K.Hardware-efficient systemization of DA-based calculation of finite digital convolution[J].IEEE Transactions on Circuits-Ⅱ：Express briefs，2006（8）：707-711.

[8]朱武，张佳民，张智明.基于并行结构分布式算法的FIR滤波器设计[J].电子测量与仪器学报，2007（4）：87-92.

[9]袁江南，徐敏.基于DSP Builder的LMS自适应滤波器设计[J].计算机应用，2009（12）：2100-2104.

[10]王法栋，刘宇.高阶数字滤波器分布式算法结构比较[J].声学技术，2009（3）：307-311.

Design of High-Speed and High-Order Digital FIR Filter Based on FPGA

Hu Anmin， Lu Shaoke， Xing Yupeng， Li Rui， Wang Yu

（College of Computer and Information Engineering， Henan Normal University， Xinxiang 453007， China）

Abstract：Compared with the expense of the linear phase frequency characteristic of Infinite Impulse Response （IIR） digital filter， Finite Impulse Response （FIR） digital filter not only ensures the accurate strict linear phase characteristic， simple structure and stable in the design and application of digital filter. But the FIR need higher order when complete the same design index， this paper proposes an improved distributed algorithm in order to meet the design of high-speed and high-order digital FIR filter. The algorithm uses the Polyphase decomposition and pipeline technology and multiplexing adder pre-add the data to reduce the Look up Table （LUT） size of the traditional distribute algorithm of mainstream Field Programmable Gate Array （FPGA） chip . The paper makes use of Matlab simulation design， Quartus II compile testing and downloads to the Field Programmable Gate Array（FPGA） to analysis， the results show that the method effectively reduces the filter to the consumption of hardware resources， can realize the high-order FIR filter in a more appropriate way.

Key words：finite impulse response filter； distribute algorithm； field programmable gate array； digital signal processing