一个(2+1)——维非线性微分方程的精确解

□张瀚文 吕 娜 隋佳辰

（大连民族大学理学院 辽宁 大连 116600）

一个(2+1)
——维非线性微分方程的精确解

□张瀚文 吕 娜 隋佳辰

（大连民族大学理学院 辽宁 大连 116600）

本文主要研究一个(2+1)——维非线性微分方程精确求解的问题。借助于符号计算软件Maple，分别利用Ricaati方程法，Exp函数法以及Tanh函数方法求得了一个非线性微分方程的精确解。

精确解；孤子理论；非线性微分方程

在非线性科学领域中的各种动态数学模型，往往可以归结为非线性微分方程。由于这些非线性微分方程能够合理地解释相关的自然现象和性质，因而一直备受数学家和物理学家的青睐。目前非线性微分方程被广泛应用于自然科学的各个领域，包括流体力学、海洋冲击波、非线性光学、离子体物理、分子生物学等等，所以对于非线性微分方程的研究无疑将会推动科学的发展。

本文将利用三种方法，Ricaati方程法 [1]，Exp函数法[2,3]和Tanh函数法[4]对以下方程进行求解

其中u=u(x,y,t),b是常数，下标表示偏导数。

1 基于 Ricaati方程法求解

首先我们利用Riccati方程法来求解方程（1），设方程（1）的行波解为

其中k,m,n是常数。将（2）式代入方程（1），则得到如下的非线性常微分方程

现在寻找方程（3）具有如下形式的解：

其中αi是稍后确定的任意常数，Φ满足Riccati方程：

其中r是常数。平衡方程（3）中最高阶线性项v""与最高阶非线性项v'2，易知m=2，因此

将（5）和（6）式代入方程（3），使得φi(i=0…6)的系数等于零，可以得到关于α0,α1,α2,k,m,l的方程组，借助Maple可以求得该方程组的解：

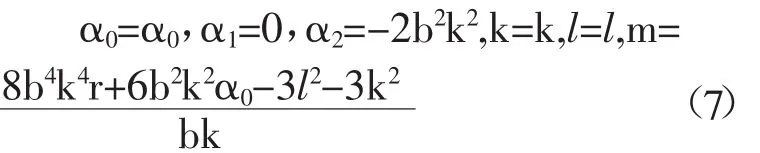
在文献[1]中，Riccati方程（5）具有如下形式的解：

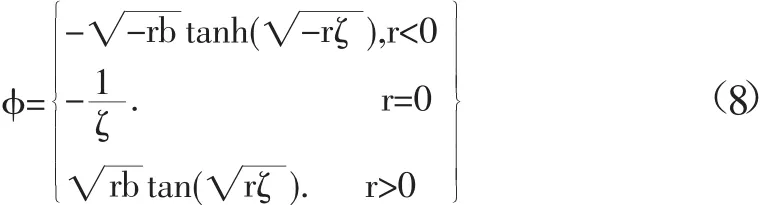
其中ζ=kx+ly+mt。

结合（7）和（8），我们得到方程（1）的精确解为：

2 基于Exp函数方法求解

将方程（1）化为方程（3），考虑方程（3）具有如下形式的精确解

其中αi,bi(i=0,1,2)是稍后确定的任意常数，基于文献[5]，经过直接的计算我们可以得到，

将（11）式代入方程（10）中即可得出方程（1）的精确解。

3 基于Tanh函数方法求解

考虑方程（3）具有如下形式的精确解：

将（12）式代入方程（3）中，利用Maple求得：

将（13）式代入方程（3）中，得到原方程的解为：

结束语

本文基于Ricaati方程法，Exp函数法和Tanh函数法研究了一个(2+1)——维非线性微分方程，并给出了该方程丰富的精确解。这三个方法对于求解非线性微分方程十分有效，能够帮助科学家们研究波的传播规律，同时为检验数值解提供了思路。

[1]X.Q.Zhao,D.B.Tang,A new note on a homogeneous balance method,Phys.Lett.A 297(2002),59-67.

[2]J.H.He,L.N.Zhang,Generalized solitary solution and compacton-like solution of the Jaulent-Miodek equations using the Exp-function method,Phys.Lett. A372(2008)1044-1047.

[3]J.H.He,X.H.Wu,Exp-function method for nonlinear wave equations,Chaos Solitons and Fractals 30(2006) 700-708.

[4]范恩贵.可积系统与计算机代数[M].科学出版社，2004.

[5]N.Lv,J.Q.Mei,H.Q.Zhang,New Explicit Solutions for(3+ 1)-dimensional Kadomtsev-Petviashvili(KP)Equation, 11(2011)506-512.

1004-7026（2016）17-0079-01

O572.23

A

10.16675/j.cnki.cn14-1065/f.2016.17.062

大学生创新创业训练计划项目（编号：S201612026051）；中央高校基本科研业务费专项资金资助项目（D C201502050403）。