多重线性回归模型在公立医院职工总人数影响因素分析中的应用
姚苏娟
多重线性回归模型在公立医院职工总人数影响因素分析中的应用
姚苏娟
目的 运用多重线性回归模型分析影响医院职工总人数的主要因素。方法 根据2013年武汉市公立医院工作量相关数据,采用逐步回归的方法,建立多重线性回归方程,进行职工总人数影响因素分析。结果 医院职工总人数受实际开放床位数和门急诊人次数影响(F=49.498,P<0.05)。从标准回归系数可知,实际开放床位数对医院职工总人数的影响最大。从R数值可知,两个自变量解释结果变量变异的70.7%,说明模型的拟合效果较好。结论 利用加权最小二乘法剔除方差因素影响后建立的多重线性回归模型在分析医院职工总人数因素中有较好的效果,结果比较准确,可以为医院相关工作者提供方法和模型参考。
多重线性回归; 逐步回归; 医院职工总人数
医院职工总人数是一项衡量医院规模、人力资源数量的重要指标,是体现和评价医院人员储备的数量指标,通过对其分析找出影响医院职工总人数的主要因素,能给医院领导或卫生行政主管部门进行相关抉择提供依据。
1 资料来源和方法
1.1 资料来源
本研究样本来源于2014武汉卫生计生年鉴所收录的武汉市地区44家公立医院职工总人数、实际开放床位数、门急诊人次数、出院病人数、住院病人手术人次数据,数据真实可信。
1.2 方法
采用逐步回归法建立多重线性回归模型对医院职工总人数进行分析。运用SPSS 21.0软件进行数据处理。
2 模型构建
2.1 模型介绍
本组选择线性回归模型,对自变量的相对重要性进行衡量[1],采用逐步回归法,以医院职工总人数(Y)为因变量,实际开放床位数(X1)、门急诊人次数(X2)、出院病人数(X3)、住院病人手术人次(X4)为变量建立多重线性回归模型(各变量具体特征见表1)。
Y=b0+b1X1+b2X2+b3X3+b4X4

表1 2013年武汉市44所公立医院指标的统计描述
2.2 检验多重线性回归的提前条件
多重线性回归模型要求数据资料满足线性、独立性、正态性和等方差性四个前提假设[2]。①用SPSS 21.0统计软件计算公立医院职工总人数影响因素数据:以职工总人数(Y)为目标,实际开放床位数(X1)、门急诊人次数(X2)、出院病人数(X3)、住院病人手术人次(X4)为预测变量进行自动线性建模,建模结果显示目标值与预测变量间具有线性相关性,准确为79.5%。②判断因变量Y(职工总人数)是否具有独立性:因变量取值若相互独立,则残差间相互独立,不存在自相关,否则不能运用多元线性回归。运用Durbin-Watson统计量判断因变量Y(职工总人数)独立性。Durbin-Watson统计取值结果(DW值)一般在0-4之间,当取值结果越接近2,则残差间越无相关性,即因变量Y越具独立性;当取值结果越接近4,则残差间负相关越强,即因变量Y不满足独立性;当取值结果越接近0,则残差间正相关越强,即因变量Y不满足独立性。用SPSS21.0统计软件计算DW值为1.507,接近2,因变量职工总人数(Y)满足独立性要求。③判断因变量Y(职工总人数)是否具服从正态分布:自变量X的任何一个线性组合,因变量Y均应服从正态分布,检验的方式是绘制标准化残差的直方图、茎叶图、正态概率分布图。本样本数据通过绘制残差直方图(Histogram)判断因变量Y(职工总人数)服从正态分布。④运用SPSS 21.0统计软件计算方差,样本数据不满足等方差性前提条件。
2.3 建立模型
SPSS21.0统计软件检验样本数据显示,样本数据满足多重线性回归模型需要满足的条件(即样本数据具备线性、独立性和正态性),但存在异方差。要得到理想的回归模型,首先要消除异方差的影响[3-4]。本组用加权最小二乘法估计偏回归系数来消除异方差的影响。

表2 检验回归模型意义方差分析表
从表2得F=49.498,P<0.05,可以判断多重线性回归模型具有统计学意义。
根据加权最小二乘法原理(即对原模型进行加权,使之成为一个新的不存在异方差性的模型,然后采用普通最小二乘法估计其参数),本样本数据运用SPSS 21.0统计软件进行逐步回归分析,得到一个包含两个自变量(实际开放床位数X1、门急诊人次数X3)的模型,模型中自变量间不存在共线性问题(见表3):方差膨胀因子VIF=3.955<4(VIF值越大多重共线性越严重,当0
从表4可以看出,自变量——实际开放床位数(X1)和门急诊人次数(X2)对因变量——职工总人数(Y)的影响具有统计学意义(P<0.05),从标准偏回归系数的大小发现,实际开放床位数(X1)对职工总人数(Y)的影响最大,其次是门急诊人次数(X2)。
综上,本样本数据多重线性回归模型可写成
Y=520.586+0.392X1+0.000X2
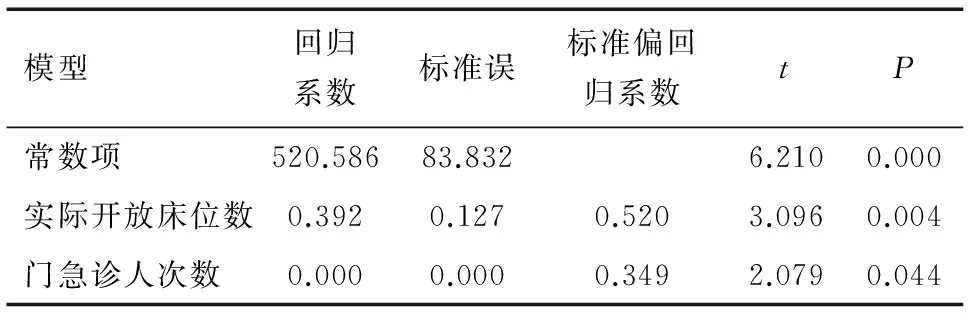
表4 回归模型的参数估计结果
3 讨论
从相关性方面看,自变量实际开放床位(X1)、门急诊人次数(X2)、出院病人数(X3)、住院病人手术人次(X4)均与因变量职工总人数(Y)有较强的正相关性,相关性程度从强到弱分别是实际开放床位数(X1)(r=0.822,P<0.05)、出院人数(X3)(r=0.817,P<0.05)、门急诊人次数(X2)(r=0.799,P<0.05)、住院病人手术人次(X4)(r=0.784,P<0.05)。经逐步回归分析,最终确定了实际开放床位数(X1)、门急诊人次数(X2)是影响医院职工总人数的两个主要因素。实际开放床位数是评价医院医疗业务量的重要指标,门急诊人次数是衡量医院诊疗工作数量的重要业绩指标之一。说明以实际开放床位数和门急诊人次数所体现的医疗业务工作量直接影响医院职工总体数量。通常实际开放床位数与医院职工总人数之间,存在线性关系,实际开放床位数增加,医院职工总人数增加;门急诊人次数与医院职工总人数之间也存在线性关系,门急诊人次数增加,医院职工总人数增加。运用多重线性回归模型分析本样本数据,显示和验证了开放床位数、门急诊人次数是影响医院职工总人数的主要因素。通过多重线性回归模型量化分析了开放床位数和门急诊人次数对医院职工总人数的影响权重,可以为医院领导或卫生行政主管部门进行相关决策提供可靠的理论依据。
多重线性回归模型可以估计自变量与因变量之间的线性关系,确定哪些自变量对因变量有影响,分析各自变量对因变量的影响程度,运用自变量预测因变量,或在控制某些自变量的前提下,进行因变量预测。该模型是应用广泛的统计分析方法,具有较高应用价值。
[1] 孙红卫,王 玖,罗文海.线性回归模型中自变量相对重要性的衡量[J].中国卫生统计,2012(12): 900-902.
[2] 方积乾.生物医学研究的统计方法[M].北京: 高等教育出版社,2007,6,170-210.
[3] 何晓群,刘文卿.应用回归分析[M].第二版.北京: 中国人民大学出版社,2007:86-95.
[4] 郭毓鹏,郭毓鹍,等.一元加权最小二乘估计处理异方差性及SAS实现[J]. 数理医药学杂志,2009,22(4): 445-446.
[5] 黄 娟.多重线性回归模型在出院人次影响因素分析中的应用[J].中国卫生统计,2014(12):1035-1036
.[6] 方积乾.卫生统计学[M].7版.北京:人民卫生出版社,2012:243-251.
R197
A
10.3969/j.issn.1671-332X.2016.10.047
姚苏娟 : 华中科技大学同济医学院医药卫生管理学院/湖北第三人民医院 湖北武汉 430030/430033
——与非适应性回归分析的比较

