计算含无关项布尔c-导数的K图方法

厉晓华， 赵建华

(1. 浙江大学 信息中心, 浙江 杭州 310027； 2. 丽水市住建局 地理信息中心， 浙江 丽水 323000)



计算含无关项布尔c-导数的K图方法

厉晓华1， 赵建华2

(1. 浙江大学 信息中心, 浙江 杭州 310027； 2. 丽水市住建局 地理信息中心， 浙江 丽水 323000)

摘要：为简化与-或-非代数系统中含无关项逻辑函数布尔c-导数的计算过程，从逻辑函数布尔c-导数的定义出发，提出了计算含无关项一阶布尔c-导数和二阶布尔c-导数的K图方法．该方法通过折叠映射K图中的填入格值，并对相应格值进行“或”运算以计算含无关项布尔c-导数．应用实例表明，该方法直观有效，且能直接得到布尔c-导数的最简与/或式．

关键词：K图；无关项；布尔c-导数；逻辑函数

LI Xiaohua， ZHAO Jianhua

(1.CampusInformationCenter,ZhejiangUniversity,Hangzhou310027，China; 2.GeomaticsCenter,HousingConstructionBureau,Lishui323000,ZhejiangProvince,China)

布尔代数系统中存在布尔减、布尔差分、布尔e-导数等特殊运算[1-2]，其中布尔c-导数在密码学函数构造[3-4]、组合电路故障检测[5]等领域应用广泛．计算布尔c-导数是各类应用的基础．文献[6]讨论了计算布尔c-导数的K图和降维K图方法，尚缺少对含任意项布尔c-导数计算方法的研究．本文从逻辑函数布尔c-导数的定义出发，提出了计算含无关项的一阶布尔c-导数和二阶布尔c-导数的K图方法．应用实例表明，该方法直观有效，且能直接得到布尔c-导数的最简与/或式．

1相关定义

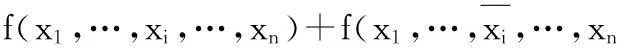
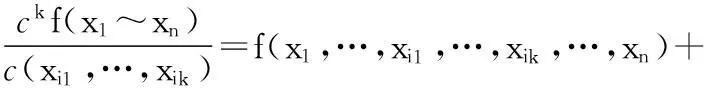
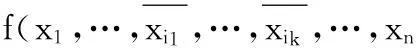
当k=2时，

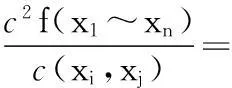
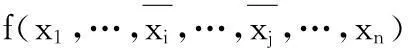
定义3逻辑函数的输入变量在某些取值下，输出函数值可以是任意的，或者这些输入变量的取值根本不会出现，其对应的最小项称为无关项．任一包含无关项的布尔函数表示为：

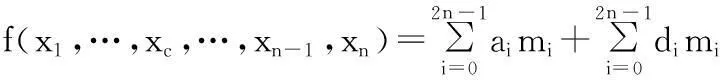
其中，∑为“或”运算，mi表示最小项，ai为最小项系数，ai∈{0,1}表示mi是否在展开中出现，di为无关项系数，di∈{0,1}表示mi是否为无关项．

2计算含无关项一阶布尔c-导数的K图方法

2.1原理

由K图特点得到计算含无关项一阶布尔c-导数的步骤如下：

(1)画出逻辑函数f(x1,…,xi,…,xn)的K图；

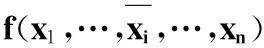
2.2实例

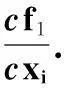
图1　一阶布尔c-导数的K图计算过程Fig.1　The calculating process of the first-order c-derivative based on K-map

cf1/cx1=∑m(0,2,3,5,7,8,10,11,13,15)+

∑d(14)+∑d6(14).

化简后得

3计算含无关项二阶布尔c-导数的K图方法

3.1原理

与计算含无关项一阶布尔c-导数的K图方法类似，计算含无关项二阶布尔c-导数的步骤如下：

(1)画出逻辑函数f(x1,…,xi,…,xj,…,xn)的K图；

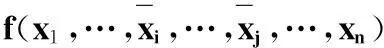
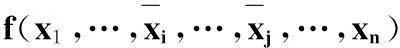
若变量xi、xj同为K图的行变量或列变量，则进行折叠映射；若一个变量为列变量，另一个为行变量，则以xi、xj轴的交点为中心进行旋转映射[7]．

3.2实例

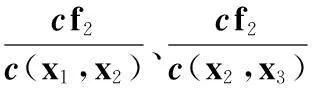
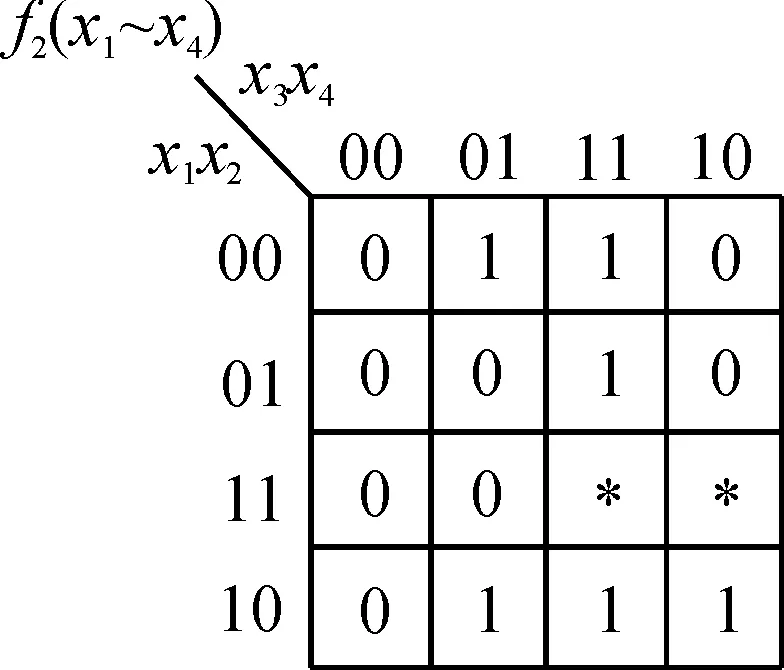
图2　逻辑函数f2(x1～x4)的K图Fig.2　The K-map of Boolean function f2(x1～x4)

图3　二阶布尔c-导数的K图计算过程Fig.3　The calculating processes of the second-order c-derivative based on K-map

∑d(14)+∑d2(14).

化简后得

c2f2/c(x1,x2)=x3+x4.

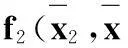
c2f2/c(x2,x3)=∑m(0,1,3,7,9,10,11,13)+

∑d(14,15)+∑d4(14)+∑d5(15).

化简后得

4结论

含无关项逻辑函数是布尔代数系统中普遍存在的一类函数，文献[8]讨论了含无关项逻辑函数布尔差分的图形化算法，文献[9]提出了含无关项布尔e-导数的新算法．本文在分析逻辑函数布尔c-导数定义的基础上，提出了计算含无关项一阶布尔c-导数和二阶布尔c-导数的K图方法，并举例说明了计算过程．虽然文中只讨论了计算含无关项一阶和二阶布尔c-导数的K图方法，但该方法亦适用于高阶布尔c-导数的计算．

参考文献(References)：

[1]陈偕雄，沈继忠. 近代数字理论[M]. 杭州：浙江大学出版社，2001.

CHEN Xiexiong, SHEN Jizhong. Modern Digital Thoery[M]. Hangzhou：Zhejiang University Press, 2001.

[2]温巧燕，钮心忻，杨义先. 现代密码学中的布尔函数[M]. 北京：科学出版社，2000.WEN Qiaoyan，NIU Xinxin，YANG Yixian. Boolean Function in Modern Cryptology[M]. Beijing: Science Press, 2000.

[3]赵美玲，陈偕雄. 布尔函数的c-导数及其在揭示H-布尔函数性质中的应用[J]. 浙江大学学报：理学版，2015，42(2):153-156.ZHAO Meiling, CHEN Xiexiong. c-derivative of Boolean functions and its application in revealing the properties of H-Boolean function[J]. Journal of Zhejiang University: Science Edition, 2015, 42(2):153-156.

[4]马汝星，陈偕雄. 布尔特殊运算c-导数及其在Bent函数研究中的应用[J]. 浙江大学学报：理学版，2015,42(2): 157-161.

MA Ruxing，CHEN Xiexiong. Boolean special operation c-derivative and its application in studying Bent function[J]. Journal of Zhejiang University: Science Edition, 2015, 42(2):157-161.

[5]王芳，应时彦，肖林荣. 布尔函数的c-导数及其在组合电路故障检测中的应用[J]. 浙江大学学报：理学版，2014, 41(2)：153-155.WANG Fang, YING Shiyan, XIAO Linrong. The c-derivative of Boolean function and its application in fault detection of combinational circuit[J]. Journal of Zhejiang University: Science Edition, 2014, 41(2):153-155.

[6]朱耀东，袁菊明，肖林荣. 逻辑函数布尔c-导数的图形计算方法[J]. 浙江大学学报：理学版，2015, 42(2)：162-165.

ZHU Yaodong，YUAN Juming，XIAO Linrong. Graphic method calculating c-derivative of Boolean function[J]. Journal of Zhejiang University: Science Edition, 2015, 42(2):162-165.

[7]陈偕雄，余党军.数字逻辑的图形方法[M]. 北京：机械工业出版社，2004.

CHEN Xiexiong, YU Dangjun. Digital Logic Graphic Methods[M]. Beijing: China Machine Press, 2004.

[8]王勇超，谢永凯. 含任意项逻辑函数布尔差分的图形化算法研究[J]. 浙江大学学报：理学版，2009, 36(6)：666-669.

WANG Yongchao，XIE Yongkai. Research of map method for Boolean difference calculation in logic functions including don’t-care-terms[J]. Journal of Zhejiang University: Science Edition, 2009, 36(6):666-669.

[9]厉晓华，杭国强. 计算布尔e-导数的新算法[J]. 电路与系统学报，2012, 17(5):1-5.

LI Xiaohua, HANG Guoqiang. The new algorithm of calculating Boolean e-derivative[J]. Journal of Circuits and Systems,2012, 17(5):1-5.

The K-map method for calculating c-derivative of Boolean function with don’t-care-terms. Journal of Zhejiang University(Science Edition), 2016,43(3):307-309

Abstract:To simplify the process for calculating c-derivative of Boolean function with don’t-care-terms in the Boolean logic algebra system based on AND-OR-NOT operation, the K-map method for calculating the first and second-order c-derivative of Boolean function with don’t-care-terms is proposed according to the definition of c-derivative. The c-derivative is calculated by folding the square corresponds of the K-map, and then conducts OR operation. The application results show that the presented method is simple and convenient for operation. The simplest AND/OR expansion of c-derivative of Boolean function with don’t-care-terms can also be obtained from K-map.

Key Words:K-map； don’t-care-terms； c-derivative； logic function

中图分类号：TP331

文献标志码：A

文章编号：1008-9497(2016)03-307-03

作者简介：厉晓华(1975-)，ORCID:http://orcid.org/0000-0003-2482-9000,男，高级工程师，硕士，主要从事数字电路与网络信息安全研究，E-mail:xiaohua@zju.edu.cn.

基金项目：国家科技支撑计划项目(2013BAH27F01，2013BAH27F02).

收稿日期：2015-06-18.

DOI:10.3785/j.issn.1008-9497.2016.03.010