六自由度微振动模拟平台动力学分析
张朴真 杨建中,2 从强 张晓东
(1北京空间飞行器总体设计部,北京 100094)(2南京航空航天大学宇航学院,南京 210016)
六自由度微振动模拟平台动力学分析
张朴真1杨建中1,2从强1张晓东1
(1北京空间飞行器总体设计部,北京 100094)(2南京航空航天大学宇航学院,南京 210016)
针对航天器的控制力矩陀螺微振动试验对通用微振动振源的需求,在分析微振动形式的基础上,提出了6-PUS并联机构的六自由度微振动模拟平台来模拟微振动试验的新思路。基于Newton-Euler法,给出了6-PUS并联平台动力学特性的分析方法,并建立了定平台输出力/力矩与支链驱动力之间的动力学模型。使用MATLAB软件对模型进行了仿真计算,并与理论计算值进行了比较分析,验证了动力学模型的正确性,可以为同类微振动模拟平台动力学与控制研究提供参考。
航天器;动力学;并联机构;微振动;振动模拟
1 引言
随着航天技术的发展,星载相机的成像分辨率由米级提高到分米级,对由星上控制力矩陀螺(CMG)引起的微振动越来越敏感。为了抑制微振动,须要研制CMG减隔振装置。本文研究的6-PUS并联机构的六自由度微振动模拟平台,可以模拟微振动力幅值1~10N,力矩幅值0.1~1Nm、一倍频频率为30~200Hz的小型CMG的微振动,从而为小型CMG减隔振装置的试验提供通用的微振动振源,以提高微振动试验的效率与有效性。
由于转速调整等运动状态的变化或动不平衡等因素的影响,CMG等运动部件在正常工作中会在安装平面产生六自由度的微振动[1]。一般的振动试验设备如单个或多个组合的激振器、振动台通常只能模拟1~3自由度的振动。Stewart并联机构通常利用动平台的六自由度运动,可实现精确指向、减隔振、空间对接等功能,在航天领域有着广泛的应用[2]。例如基于Stewart并联机构的飞行模拟器[3],小型六支链精确指向平台[4]等。根据达朗贝尔原理,Stewart平台也可以利用定平台输出六自由度的力/力矩,即实现安装面的六自由度振动模拟。其中,6-PUS并联机构作为Stewart并联机构的一种构型,具有更低的运动支链质量、更小的转动惯量、更快的响应速度。根据上述分析,本文提出了一种微振动试验的新思路,即采用6-PUS并联机构来模拟六自由度的微振动试验。
Yang[5]等人在忽略支链转动惯量的条件下,研究了Stewart并联机构的逆动力学问题。Dasgupta[6-7]等人通过矢量投影等方法提高了动力学模型的运算效率,并进一步给出了相应的控制算法。Geng[8]等人给出了形式较为简单整齐的Stewart并联机构的动力学模型。黄真[9]等人采用影响系数法研究了并联机构的运动与受力,并建立了动力学模型。上述研究主要是围绕驱动力与动平台运动之间的关系建立动力学模型,并未涉及定平台的输出力/力矩。
本文基于Newton-Euler法,针对定平台输出力/力矩问题,研究了六自由度微振动模拟平台的运动学、动力学特性,建立了微振动模拟平台的动力学模型,从而得到定平台输出力/力矩与驱动力的关系。在SimMechanics模块中对所需输出力/力矩对应的驱动力进行了计算,将计算结果代入机械系统模型中,仿真此时的输出力/力矩,并对所需输出值与实测输出值进行了比较,验证了建模方法的正确性以及6-PUS并联机构用作微振动试验模拟平台的可行性。
2 动力学建模方法
六自由度微振动试验模拟平台由定平台、六条支链、动平台3部分组成。平台采用立方体构型,即六条支链的初始位置为正方体的六条棱,依次将各条支链编号,如图1所示。每条支链分为3部分,即下支链、中支链、上支链。下支链下端与定平台固连,下支链上端用移动副与中支链下端相连,中支链上端用万向节与上支链下端相连,上支链上端用球铰与动平台相连,其中移动副为驱动副。
为了方便描述六自由度微振动模拟平台的立方体构型,并简化支链的坐标表示,建立绝对坐标系O-xyz,即{O},如图1所示,3条坐标轴分别对应立方体的3条正交棱。由于输出力/力矩方向是相对于定平台描述的,建立定平台坐标系OB-xByBzB,即{OB},OB可以认为是定平台力/力矩输出点。建立动平台的固连坐标系OP-xPyPzP,即{Op},Op为动平台中心。
由于各条支链结构相同,位置对称,具有相同动力学方程,因此下文的支链动力学中不区分具体支链。六自由度微振动模拟平台的位置逆解、运动学逆解较为复杂,此处不再展开论述,下文推导中涉及到的相关变量直接作为已知量处理。
2.1 支链动力学
如图2所示,万向节的角速度始终在u1、u2所在平面内,因此万向节对上支链的约束力矩大小为MU,方向为u3,约束力为FU。移动副对中支链的约束力为FC,约束力矩为MC;驱动力大小为FA,方向矢量为n1。
分别以中支链、上支链为研究对象,可知:
式中:mu、md,au、ad分别为上支链、中支链质量和质心加速度,g为重力加速度,为万向节加速度,FS为动平台对上支链的约束力。
由于中支链被移动副约束,不存在转动,根据动量矩定理,外力对下支链移动副中心取矩得

式中:L2为移动副中心指向万向节中心的矢量。将上支链所受外力对万向节中心取矩:

式中:x为FS沿n3的分量大小,C为FS非n3方向的分量。
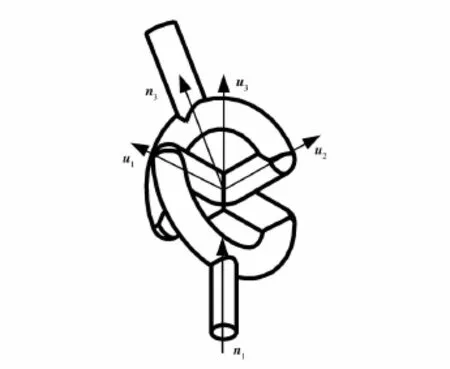
图2 中支链与上支链之间的万向节Fig.2 Universal joint between middle and upper part of the leg
2.2 平台动力学
动平台除了受重力、球铰的支持力之外,没有其它外载荷,因此力/力矩平衡方程为
式中:m为动平台质量,a为动平台质心加速度,ωp、α分别为动平台角速度、角加速度,X为动平台对球铰的约束力矢量,由各条上支链轴线上的分量组成,为动平台在{O}中相对质心的转动惯量,JP为与动平台对应的雅克比矩阵。
由于振动模拟平台采用了立方体构型,且微振动幅值较小,动平台的位姿变化很小,雅克比矩阵JP始终可逆,由式(6)可解得X,代入式(5),可以求得动平台对上支链的约束力FS,将FS代入式(1)~(4)中,得到每条支链各运动副的约束力与约束力矩。
在{OB}中定义输出力/力矩:FB、MB,可得各支链驱动力组成的矢量为
式中:ROB为定平台坐标系到绝对坐标系的坐标变换矩阵,mAi为支链驱动装置(固连在定平台上)的质量;FCi为移动副对下支链的约束力,Bi为定平台中心到各下支链下端的矢量,L3i为下支链下端指向移动副中心的矢量,其中i为支链编号,JB为与定平台对应的雅克比矩阵。
3 SimMechanics机械系统仿真
应用MATLAB软件中的SimMechanics模块,可以建立模块化的机械系统模型[10]。本文对六自由度微振动模拟平台动力学模型的验证,就是通过理论计算结果与SimMechanics模块中建立的机械系统模型运行结果相比较。
按照第2节所述的关节顺序,将各支链分别与定平台、动平台相连;设定各构件的运动、运动约束、坐标系统,初始化系统的运动状态;在移动副处设置驱动模块,提供所需的驱动力;在动平台处添加传感器模块,仿真其位移、速度、加速度,以及角度、角速度、角加速度,为第2章建立的动力学模型提供输入;在定平台中心点设置力传感器,仿真该点处力/力矩的输出,组成六自由度微振动模拟平台机械系统,如图3所示,上方的三角形为动平台,中间的六根线为6条支链,下方的三角形为定平台。
SimMechanics模块与任何Simulink软件设计的控制器及其它动态系统相连,从而可以进行综合仿真分析。因此,可以在Simulink软件中搭建第2节所述的动力学模型,将该动力学模型引入到Sim-Mechanics模块中建立的六自由度微振动模拟平台机械系统模型,验证动力学模型的正确性。
4 仿真结果与动力学模型分析结果对比
假设支链初始总长度为200mm,动平台质量为3kg,上、中支链质量均为0.03kg,下支链即驱动装置质量为0.5kg,在SimMechanics模块中建立振动模拟平台的机械系统模型。将规定的定平台输出代入到动力学模型中,求解振动模拟平台的移动副的驱动力,通过仿真定平台的输出力是否与所需的定平台输出力一致,来检验动力学模型的正确性。
以某CMG的微振动试验数据为例,该CMG的转速为6000r/min,即微振动的一倍频为100Hz。在{OB}中定义微振动模拟平台的3种工况:工况1为一自由度微振动输出,工况2为三自由度微振动输出,工况3为六自由度微振动输出,如表1所示。

表1 微振动模拟平台的3种工况Table 1 Three working conditions of the micro-vibration simulation platform
表1中,Fx、Mx,Fy、My,Fz、Mz分别为沿{OB}各坐标轴方向输出力/力矩。ω为振动频率,大小为100Hz;G为动平台、支链和驱动装置所受的重力之和,大小为-62.3916N。
4.1 工况1分析
根据工况1中的输出要求,求解动力学方程得到各支链的驱动力,如图4(a)所示,各支链驱动力的频率、相位、幅值均相同,产生z向同频率的余弦力,且均有一个正向偏差,可以克服重力。测量定平台的输出力/力矩,如图4(b)所示,其中z轴的输出与工况一相符。所需输出力/力矩减去测量得到的实际定平台输出力/力矩,得到振动模拟平台输出误差,如图4(c)所示,最大的误差为10-7量级,可以忽略。
4.2 工况2分析
根据工况2中的输出要求,求解得到各支链的驱动力,如图5(a)所示,1、2、3支链与6、5、4支链相位相差π,可以产生y轴方向的力矩和x轴方向的合力。测量定平台的输出力/力矩,如图5(b)所示,其中x、z轴的输出力和y轴的输出力矩与工况2相符。如图5(c)所示,振动模拟平台的输出误差量级为10-14,可以忽略。
4.3 工况3分析
根据工况3中的输出要求,求解得到各支链的驱动力,如图6(a)所示。测量定平台的输出力/力矩,如图6(b)所示,其中各轴的输出力与输出力矩与工况3相符。如图6(c)所示,振动模拟平台的最大输出误差量级为10-14,可以忽略。
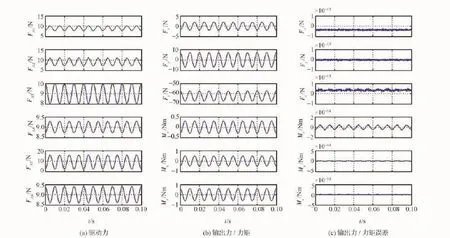
图6 工况3仿真结果Fig.6 Simulation results of the third working condition
3个工况中,各支链驱动力、定平台输出力/力矩与规定的工况相符,可以满足微振动输出的要求,证明了动力学模型的正确性。同时表明,6-PUS并联机构具备单自由度/多自由度力/力矩的输出能力,可以作为微振动模拟平台来模拟CMG的六自由度微振动。
5 结束语
相对于现有的振动试验设备,本文研究的6-PUS并联机构的六自由度微振动模拟平台可以更全面地模拟CMG六自由度的微振动。同时振动模拟平台的振动幅值、频率在一定范围内可调,可以充分地检验减隔振装置抑制不同大小、不同频率微振动的能力。由于振动产生的原理不同,在试验过程中振动模拟平台起振速度更快,节约了等待CMG升降速的时间,可以显著地提高试验效率、降低试验成本。
本文通过建立6-PUS微振动模拟平台的动力学模型,给出了输出力/力矩与驱动力之间的关系,并通过构型、支链运动副顺序的选择,简化了微振动模拟平台的动力学模型;使用MATLAB软件相关模块求得了与定平台输出力/力矩对应的各支链驱动力,并对振动模拟平台的典型工况进行了验证,结果表明理论计算值与仿真值相符,证明了采用6-PUS微振动模拟平台新思路的可行性,为进一步的微振动模拟平台详细设计打下了基础,并可为同类平台动力学与控制的研究提供参考。
(
)
[1]R A Masterson,D W Miller,R L Grogan.Development of empirical and analytical reaction wheel disturbance moels[C]//Structures,Structural Dynamics and Materials Conference and Exhibit.St.Louis:American Institute of Aeronautics and Astronautics,1999:1-12
[2]杨建中.Stewart并联机器人在航天器上的应用[C]//全国第十二届空间及运动体控制技术学术会议.北京:中国自动化学会,2006:426-431 Yang Jianzhong.Applications of the stewart parallel manipulator on space vehicles[C]//The 12thNational Space and Motion Control Technology Conference.Beijing:Chinese Association of Automation,2006:426-431(in Chinese)
[3]D Stewart.A platform with six degrees of freedom[J].Proc.Inst.Mech.Engrs.,1965,180(15):371-386
[4]Brown,Alan S.Six-axis positioner has nanoscale resolution[J].Mechanical Engineering,2010,5(5):19-19
[5]W Q D Do,D C H Yang.Inverse dynamic analysis and simulation of a platform type of robot[J].Journal of Robotic Systems,1988,5(3):209-227
[6]B Dasgupta,T S Mruthyunjaya.A newton-euler formulation for the inverse dynamics of the stewart platform manipulator[J].Mech.Mach.Theory,1998,33(8):1135-1152
[7]B Dasgupta,T S Mruthyunjaya.Closed-form dynamic equations of the general stewart platform through newton-euler approach[J].Mech.Mach.Theory,1998,33(7):993-1012
[8]Z Geng,L S Haynes,J D Lee,et al.The dynamic model and kinematic analysis of a class stewart platforms[J].Robotics and Autonomous Systems,1992,9(4):237-254
[9]黄真,赵永生,赵铁石.高等空间机构学[M].2版.北京:高等教育出版社,2014 Huang Zhen,Zhao Yongsheng,Zhao Tieshi.Advanced spatial mechanism[M].2nd ed.Beijing:Higher Education Press,2014(in Chinese)
[10]薛定宇,陈阳泉.基于MATLAB/Simulink的系统仿真技术与应用[M].北京:清华大学出版社,2011 Xue Dingyu,ChenYangquan.System simulation technology and application based on MATLAB/Simulink[M].Beijing:Tsinghua University Press,2011(in Chinese)
(编辑:李多)
Dynamic Analysis of a 6-DOF Micro-vibration Simulation Platform
ZHANG Puzhen1YANG Jianzhong1,2CONG Qiang1ZHANG Xiaodong1
(1Beijing Institute of Spacecraft System Engineering,Beijing 100094,China)
(2College of Aerospace Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China)
Based on the analysis of micro-vibration performance,a new method that the 6-PUS parallel mechanism is used as a micro-vibration simulator is presented to satisfy the demand of spacecraft's control moment gyroscope micro-vibration test.The analysis of 6-PUS parallel mechanism dynamics problem and the dynamic model between the force of the fixed platform and the power of the actuators are given based on the Newton-Euler approach.The comparison and analysis of simulation results of MATLAB and the required output prove the validity of the dynamics model,which has reference value for the study of dynamics and controls of similar micro-vibration simulators.
spacecraft;dynamics;parallel mechanism;micro-vibration;vibration simulation
TH112
A
10.3969/j.issn.1673-8748.2016.02.004
2015-12-01;
2016-01-13
国家重大科技专项工程
张朴真,男,硕士研究生,研究方向为航天器结构与机构。Email:zpz.1989@163.com。

