采用响应曲面法的纱线空气捻接参数优化

吴震宇，陈小天，石鹏飞，王冠华，胡旭东

(浙江理工大学 浙江省现代纺织装备重点实验室,浙江 杭州 310018)

采用响应曲面法的纱线空气捻接参数优化

吴震宇，陈小天，石鹏飞，王冠华，胡旭东

(浙江理工大学 浙江省现代纺织装备重点实验室,浙江 杭州 310018)

为了分析捻接压力、退捻时长以及纱头重叠长度对捻成纱线强力保持率的影响规律，设计以这3项影响因素为因子的正交试验，并对试样进行断裂强力测试，得到了强力保持率的响应曲面模型。根据该模型，分析了捻接压力、退捻时长以及纱头重叠长度对捻成纱强力保持率的交互影响规律。结果表明：相比于退捻时长，捻接压力与纱头重叠长度对捻成纱线强力保持率的影响更为显著；按优化所得工艺参数进行配置，捻接纱线强力能够达到原纱强力的87.85%。

空气捻接；强力保持率；响应曲面法；优化设计

空气捻接是一项能够有效提高纱线质量的纺织工艺技术，用于2段分离纱线的连接。纱线空气捻接过程较为复杂，首先产生高速射流使待捻接的2段纱线各自退捻，解除原纱头端捻度，使其构成纤维处于平直状态，再通过牵引机构将2段去捻线头以一定长度相互重叠，运用反向气流使2段分离纱线的构成纤维须头相互缠绕、连接而形成单一纱线，完成捻接过程。空气捻接成纱质量是细观尺度上受气流作用的大量纤维变形及相互缠绕的体现，因此，影响纱线捻接效果的因素较多，如捻接气体压力、退捻持续时长、纱线重叠长度、环境温湿度以及纱线性质等都会对其产生直接影响[1-2]。

鉴于捻接工艺对纱线准备工序的重要性，国内外许多学者对该项技术展开了研究。李志锋等[3]对空气捻接器基本原理以及影响捻接成纱质量的主要因素进行了定性说明，Unal等[4-5]针对空气捻接质量进行了深入研究，重点围绕捻成纱线直径和强力2个纱线捻接指标，分析了不同因素对捻接质量的影响规律。Webb等[6]运用高速摄影机观察水流驱动纤维产生缠绕过程，通过可视化方式分析对纤维捻接形成过程。

使用气流驱动纱线或纤维来实现纺织品成形控制也是纺织机械中常见的方式。Meulemeester等[7]对射流中被牵引飞行的纱线动态特性进行建模，分析了纱线飞行过程中的动力学行为。随着近年来计算流体力学技术的发展，很多学者对气体流道中空气流动特性进行数值模拟，Guo等[8]对不同结构涡流纺喷嘴内气流流动模式进行了对比，根据不同流道所诱导的流场发展趋势进行了详细分析；Juraeva等[9]运用计算流体力学理论对空气捻接器流道内气体流动进行分析，并根据流动特点给出了捻接器流道尺寸和形状的优化设计方法。由于纱线或纤维是受气流作用的直接对象，因此，也有一些学者采用流固耦合理论对气流场中的纤维运动进行分析。Pei和Guo等[10-11]分别采用流固耦合理论对纺纱喷嘴中的气流发展及其内部纱线运动进行数值建模和运动分析，得到了纤维瞬态运动弯折规律，推动了对受气流作用纤维运动的进一步理解。但是，纱线捻接过程较纺纱过程更为复杂，涉及到成束纤维缠绕，运用流固耦合方法对纱线捻接过程的纱线运动和气流发展进行建模分析尚存在一定困难。

目前，企业生产过程中主要以经验为主，通过生产记录、肉眼观察和人为估计等方法确定捻接工艺参数，受随机因素干扰较大，无法快速准确的找到最优工艺参数配置。为了分析退捻时长、纱头重叠长度以及捻接气压对捻成纱线强力保持率的影响规律，确定生产过程中最优工艺参数，本文以这3个影响因素为设计因子，进行了三因子三水平正交试验设计。根据试验设计的结果进行棉纱线试样的捻接试验，利用纱线强力测试仪进行试样断裂强力值的测试。利用响应曲面法对试验结果进行回归分析，得到了强力保持率的响应曲面模型。根据响应曲面模型，分析了退捻时长、纱头重叠长度以及捻接气压对捻成纱强力保持率的交互影响规律，并对工艺参数进行优化。

1 空气捻接装置工作原理

1.1 基本工作原理及工艺参数调节

以MESDAN690型自动空气捻接器和Z向捻40 tex棉纱线为试验仪器及材料，空气捻接装置系统构成以及其工作原理如图1所示，2段待捻接纱线被平行放置在空气捻接腔内，纱头穿过呈对称分布的一对纱固定器和剪刀；在机构运动带动下剪刀将纱头前端多余部分剪断，接通退捻气路，在气流作用下纱头被吹入退捻管并在旋转管道中完成退捻，形成纤维须条平行的退捻纱头；其后在机构继续运动下，引纱器将纱头拉入加捻腔。压缩气体经由加捻流道后，形成和退捻气流方向相反的加捻气流，使两端退捻纱头的纤维须条互相包缠，完成缠绕捻接。

空气捻接不同工作阶段的动作时序由步进电动机回转过程中的速度和角度进行控制。步进电动机与凸轮轴固连，带动凸轮轴转动，使各连杆按照特定时序运动，从而控制内部气路的通断以及外部组件工作。试验过程中通过改变步进电动机的转动速度和角度，分别改变退捻气路打开时间以及引纱器运动行程，从而调节退捻时长和纱头重叠长度2个工艺参数。

1.2 测试指标

采用捻成纱断裂强力值来表征空气捻接成纱质量。根据GB 6529—1986《纺织品的调湿和试验用标准大气》进行测试。试验前先剪取20个长为15 cm的原纱进行强力测试，取强力平均值并记为Q0，则Q0为原纱强力值；将试验所得的捻成纱强力值记为Qn，捻接强力保持率记为η，其表达式为

(1)

2 试验及结果

根据前期预备性试验结果以及空气捻接器的推荐设置，粗略确定3个因子的试验范围。采用Box-Behnken试验设计方法设计三因素三水平试验，如表1所示。

表1 Box-Behnken试验因子水平及其编码Tab.1 Level and code of variables for Box-Behnken design

利用Minitab软件进行试验设计，试验安排以及测量结果如表2所示。

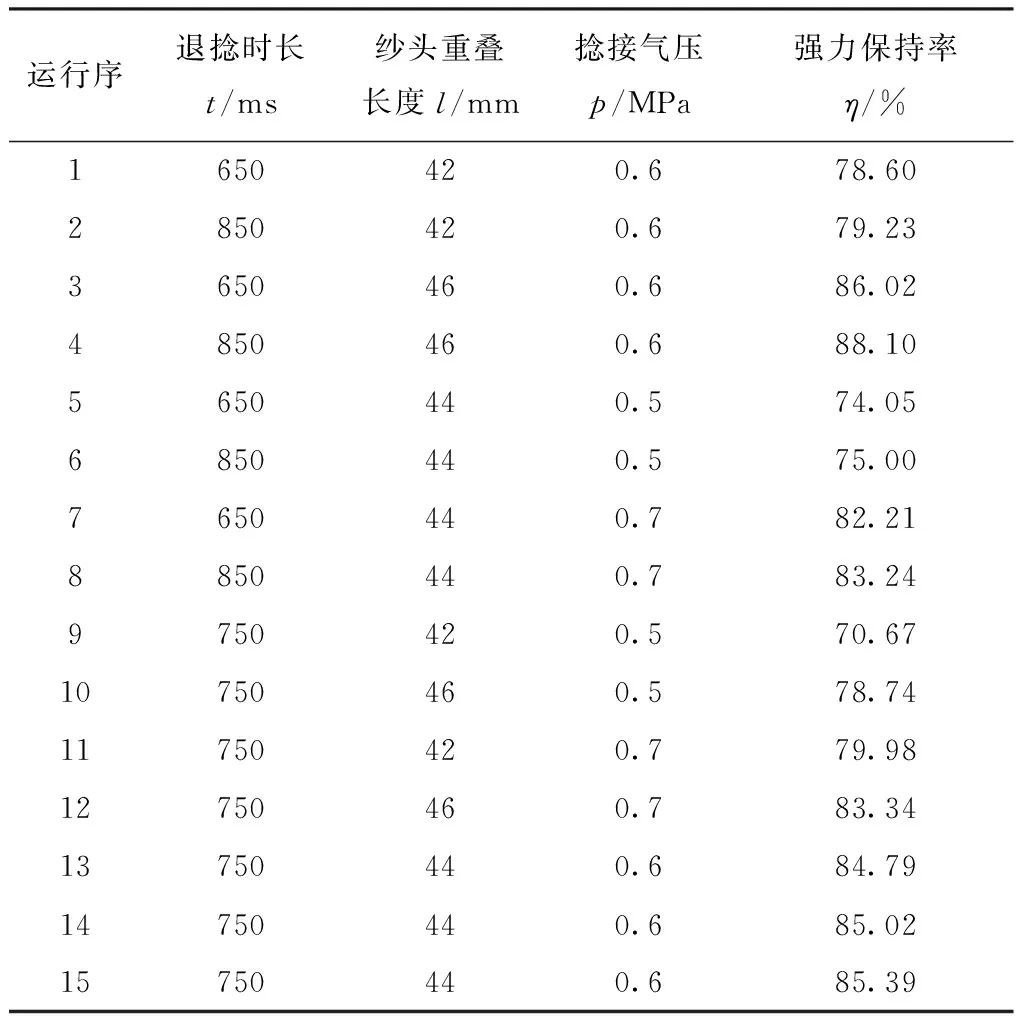
表2 试验设计及试验结果Tab.2 Experimental design and results

3 结果与分析

3.1 模型方差分析和检验

为分析3个因素的一次、二次以及交互作用对纱线捻接强力保持率的影响规律，本文建立了完全二次回归模型，该模型数学表达式为

(2)

式中：η为捻接强力保持率；t、l和p分别为退捻时长、纱头重叠长度以及捻接气压3项影响因素；β0为常数项，βt，βl，βp为三因素的一次项系数、βtt，βll，βpp为三因素的二次项系数，βtl，βtp，βlp为三影响因素的交互项系数；ε表示误差(包括试验误差和拟合误差)。模型的方差分析结果如表3所示。

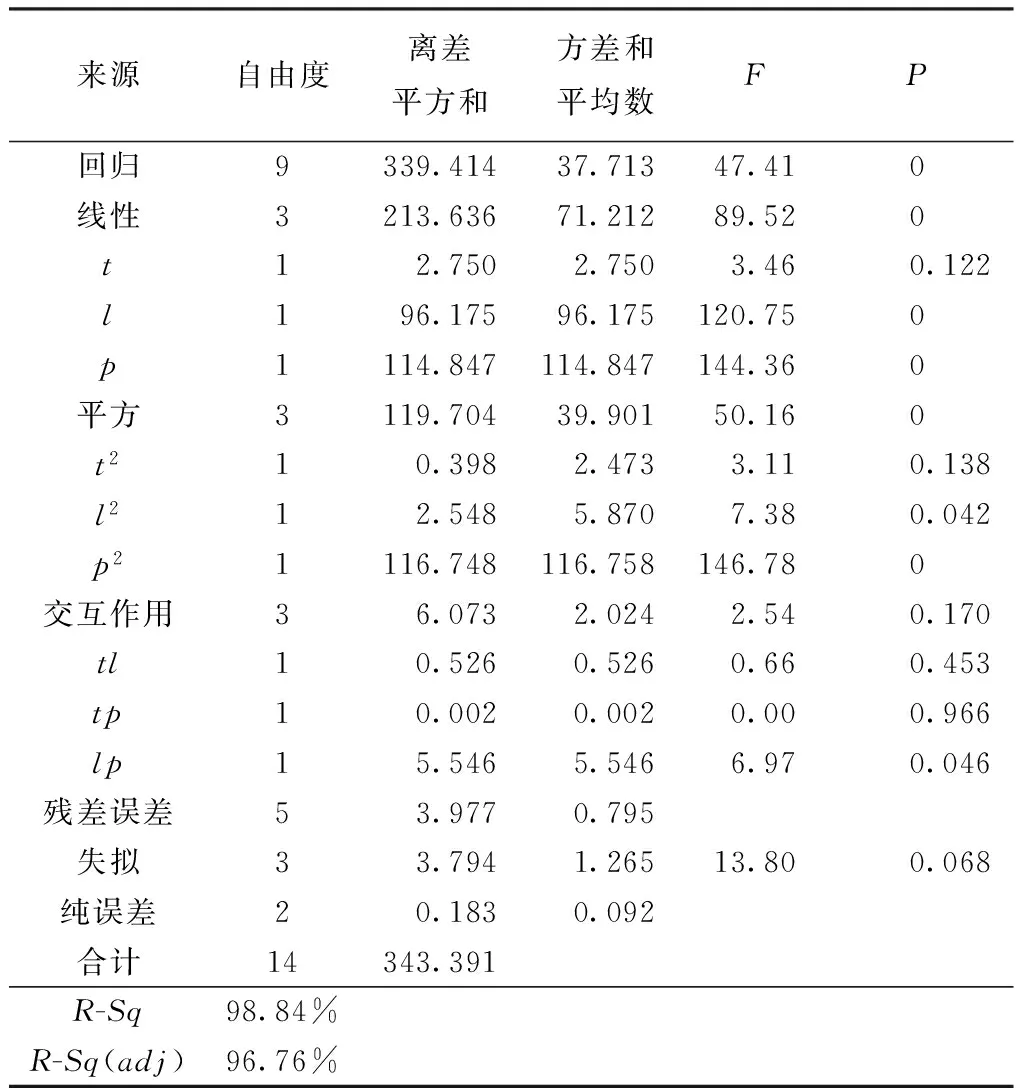
表3 回归模型及其各项的方差分析Tab.3 Analysis of variance(ANOVA) for regression model and factors

根据方差分析结果可获得回归模型的各项系数值，将各系数值代入式(2)得到完整的回归模型表达式：

η=-971.73+0.05t+31.64l+97.02p-

8.18t2-0.32l2-5.62p2+0.002tl+

0.000 2tp-0.59lp

(3)

由统计学假设检验原理可知，P值反映了观察到的实际数据与原假设之间不一致的概率[12]，当P>0.05，表明对应项不显著，P<0.05则认为对应项显著，P<0.01则认为对应项高度显著。

由表3可知，回归项的P值为0.000，表明所建模型回归效应高度显著；模型失拟项的P值为0.068，大于0.05，表明无法拒绝原假设，失拟项对响应影响不显著，即模型失拟率很小；调整后的多元全回归系数R-Sq(adj)为96.76%，即总误差中仅有2.08%的误差不能通过此模型解释，表明该模型与实际情况拟合良好，可以用来做空气捻接器的捻接成纱质量理论预测。

从表3的回归方程系数显著性检验可知：一次项l和p高度显著；二次项l2显著，p2高度显著；交互项lp显著；其余各项均不显著。剔除模型的不显著项，得到捻成纱的强力保持率η随各因素变化关系的二次回归方程模型：

η=-971.73+31.64l+97.02p-0.32l2-

5.62p2-0.59lp

(4)

3.2 退捻时长的作用影响

退捻时长和纱头重叠长度、捻接气压对强力保持率的响应曲面如图2、3所示。在纱头重叠长度l或捻接气压p变化条件下，随着退捻时长的增加，响应曲面未出现明显弯曲，即退捻时长对纱线强力保持率影响不显著，符合所建模型描述。

产生上述现象的主要原因在于退捻管内气流发展极为迅速。采用计算流体力学软件FLUENT对退捻管内部气流流动进行瞬态流动仿真计算，单步时间步长为1.2 ms。图4示出退捻腔出口质量流量随时间变化曲线。可以看出，退捻腔出口处的气流质量流量小，在计算迭代步数达到454步后保持稳定，整个发展过程持续时长为544.8(454×1.2)ms，因此，在试验典型的退捻时长650～850 ms内，气流均能得到完全发展，对纱线进行充分退捻。

3.3 纱头重叠长度和捻接气压的作用影响

图5示出纱头重叠长度和捻接气压对捻接强力的响应曲面与等高线图。可以看出，捻接气压和纱头重叠长度对强力保持率的影响为非线性，响应曲面出现弯曲，且随着p和l的增大，强力保持率逐渐增大。由图5(b)观察到，这2个因素间存在交互作用，即在单一因素变化时，为保持较大捻接强力，捻接气压和纱线重叠长度间应保持同步变化。原因在于捻接气压决定退捻纱线长度。随着捻接气压增大，被退捻纱线长度增加，要获得较高捻接强力，则需要增大重叠长度，使纤维须条充分缠绕。

试验过程中还发现，在捻接强力极大值区域附近，纱线呈现出2种不同的缠绕模式。如图6所示。捻成纱线纤维须条互相包缠，捻成纱表面呈螺旋状，结合面较为光滑，捻接部位直径约为原纱的1.2倍；而如图7所示，捻接以纱线主干互相缠绕为主，捻成纱纤维须条与纱线主干包缠，捻接部位约为原纱直径的1.5倍。

2种捻接缠绕模式导致了拉伸变形过程中的纱线断裂强力变化趋势差异。图8、9是2种缠绕模式强力试验获得的伸长率-负荷曲线图。可以看到：在须条缠绕模式下，随着伸长率的增加，纱线负荷增加到峰值后迅速下降；而主干缠绕模式则在达到峰值后出现短暂稳定，而后纱线断裂负荷减小至零，且负荷峰值略小于第1种缠绕模式。

4 参数优化

为求得模型在试验范围内的最大值，令完整的回归模型表达式(式(3))分别对3个变量求偏导并使其等于零，得到方程组：

(5)

求解方程组得到响应曲面方程的驻点，再根据各驻点处的二阶偏导数值，即可求得响应函数的最值点及最大值。

根据以上方法求解所建模型在给定区域范围内的最大值。结果表明，当退捻时长为807 ms，纱线重叠长度为46 mm，捻接气压为0.623 MPa时，理论上捻成纱强力保持率能达到最大值的87.85%，符合大于85%的生产要求。

观察发现，试验组4中捻成纱强力保持率大于最优解得到的理论强力保持率。响应曲面法根据所得试验数据采用数理统计方法进行回归模型参数估计得到最优模型，可认为利用该模型求得的最优解在概率分布上呈现最优，在实际应用中出现的概率稳定，且受随机因素的干扰最小；试验组4的结果虽比优化结果大，但是该试验结果比优化结果出现的概率小，具有较大的随机性和不稳定性，因此，不宜将该组试验参数作为最优工艺参数。

在该优化条件下进行试验验证，重复试验10次，所得捻成纱平均强力保持率为86.53%，与预测值十分接近，因此，该工艺参数具有实际指导意义。

根据响应曲面试验结果，在实际生产过程中，应先调整纱头重叠长度和捻接气压，得到外观为须条缠绕模式的纱线，再适当调整退捻时长，进一步改善纱线捻接强力。

5 结 论

为了分析退捻时长、纱头重叠长度以及捻接气压对捻成纱线强力保持率的影响规律，以这3个影响因素为设计因子进行了三因子(三水平)正交试验设计。根据试验设计的结果进行棉纱线试样的捻接试验，利用纱线强力测试仪测试试样的断裂强力值；利用响应曲面法对试验结果进行回归分析，得到了强力保持率的响应曲面模型。

1)利用响应曲面法中的Box-Behnken方法进行试验设计并对空气捻接过程中各影响因素进行评价后发现，各因素对捻成纱强力保持率的显著性顺序为：捻接气压>纱头重叠长度>退捻时长。强力保持率随纱头重叠长度的增大而增大，随捻接气压的增大呈现出先增大后减小的趋势，而退捻时长则对响应值的影响不够明显，因此，在生产过程中，应先确定纱头重叠长度和捻接气压，再调整退捻时长，以得到较好的捻接成纱质量。

2)通过试验得到3个影响因素和捻成纱强力保持率之间的数学模型，其中纱头重叠长度和捻接气压2个因素之间存在显著的交互作用；在不同的重叠长度下，纱线会出现2种缠绕模式，分别为纤维须条缠绕和主干缠绕，2种模式下获得的强力值接近，考虑到捻成纱外观，选择较短重叠长度产生须条缠绕更为合适。

3)求解所建模型在试验范围内的最大值，当退捻时长为807 ms，纱头重叠长度为46 mm以及捻接气压为0.623 MPa时，捻成纱强力保持率最大，能达到87.85%。

FZXB

[1] WU Zhenyu,TIAN Fangyuan,HU Xudong.Effect of groove on performance of splicing fiber in air splicer[C]//2011 International Conference on Textile Engineering and Materials.Swiss: Advanced Materials Research,2011: 1374-1377.

[2] WEBB C J,WATERS G T,THOMAS A J,et al.Optimising splicing parameters for splice aesthetics for a continuous filament synthetic yarn[J].Textile Research Institute,2009,100(2): 141-151.

[3] 李志锋，陈瑞琪.空气捻接机理及空气捻接器的研制方向[J].纺织学报,1997,18(4): 209-211.LI Zhifeng,CHEN Ruiqi.Principle of air splicing and research direction of air splicer[J].Journal of Textile Research,1997,18(4): 209-211.

[4] UNAL P G,OZDIL N,TASKIN C.The effect of fiber properties on the characteristics of spliced yarns part I: prediction of spliced yarns tensile properties[J].Textile Research Journal,2009,80(5): 429-438.

[5] UNAL P G,ARIKAN C,OZDIL N,et al.The effect of fiber properties on the characteristics of spliced yarns: part II: prediction of retained spliced diameter[J].Textile Research Journal,2010,80(17): 1751-1758.

[6] WEBB C J,WATERS G T,THOMAS A J,et al.The use of visualization and simulation techniques to model the splicing process[J].Journal of the Textile Institute,2010,101(10): 859-869.

[7] MEULEMEESTER S D,PUISSANT P,LANGENHOVE L V.Three-dimensional simulation of the dynamic yarn behavior on air-jet looms[J].Textile Research Journal,2009,79(18): 1706-1714.

[8] GUO H,AN X,YU C.A numerical and experimental study on the effect of the cone angle of the spindle in murata vortex spinning machine[J].Journal of Fluids Engineering,2008,130(3): 135-140.

[9] JURAEVA M,SONG D J,RYU K J.An optimum design study of the yarn-channel shape of the air-interlacing nozzle by analysis of fluid flow[J].Textile Research Journal,2012,82(5): 474-483.

[10] PEI Z,HU B,DIAO C,et al.Investigation on the motion of different types of fibers in the vortex spinning nozzle[J].Polymer Engineering & Science,2012,52(4): 856-867.

[11] GUO H F,XU B G,YU C W,et al.Simulating the motion of a flexible fiber in 3D tangentially injected swirling airflow in a straight pipe effects of some parameters[J].International Journal of Heat and Mass Transfer,2011,54(21/22): 4570-4579.

[12] 费宇,石磊.统计学[M].北京: 高等教育出版社,2010: 92.FEI Yu,SHI Lei.Statistics[M].Beijing: China Higher Education Press,2010: 92.

Parameters optimization of air splicing by response surface method

WU Zhenyu，CHEN Xiaotian，SHI Pengfei，WANG Guanhua，HU Xudong

(ZhejiangProvincialKeyLaboratoryofModernTextileMachinery,ZhejiangSci-TechUniversity,Hangzhou,Zhejiang310018,China)

In order to study the effect of untwisting time,overlapping length of separation yarns and inlet pressure on the splice retained strength of splicing yarn,the orthogonal experiment design of three factors and three levels was carried out by using untwisting time,overlapping length of separation yarns and inlet pressure as the design factors.According to breaking strength of the spliced yarns,the response surface model of splice retained strength was obtained.On the base of the response surface model,the interaction effects of untwisting time,overlapping length of the spliced yarns and inlet pressure on splice retained strength were discussed.The results show that inlet pressure and overlapping length of the spliced yarns have more significant influence on the splice retained strength of spliced yarn than untwisting time.87.85% of yarn′s strength can be remained on the spliced yarn by applying the optimized parameters from the response surface model.

air splicing; splice retained strength; response surface method; optimization design

10.13475/j.fzxb.20141005606

2014-10-23

2015-08-11

国家自然科学基金资助项目(51275482)

吴震宇(1978—)，男，副教授，博士。主要研究方向为纺织装备控制技术。E-mail：zistwuzhenyu@163.com。

TS 103.11

A