基于时间窗的出行旅游规划问题研究
杨晓芳 余婷

摘 要:针对带时间窗旅游线路规划问题,以网络优化和数学规划理论为基础,建立相应的数学模型,通过对游客旅游中的时间和费用进行分析,设计出了具体路线方案,以保证旅游体验最佳。仿真结果表明,利用蚁群算法求解能使出行时间最短、费用最低、旅游体验最优等问题。
关键词:线路规划;时间窗;蚁群算法;仿真
中图分类号:F592.68 文献标识码:A
Abstract: In view of the tourist route planning problem with time windows, on the basis of network optimization and mathematical programming theory, establish the corresponding mathematical model, the analysis of tourists travel time and the cost, designed the concrete route plan, to ensure the best travel experience. The simulation results show that using ant colony algorithm can make the shortest travel time, lowest cost, travel experience the most superior.
Key words: route planning; time windows; ant colony algorithm; simulation
0 引 言
传统旅行商问题(TSP)是指推销人员要走访多个地点时,如何找到在到达每个地点一次后再回到原点的最短路
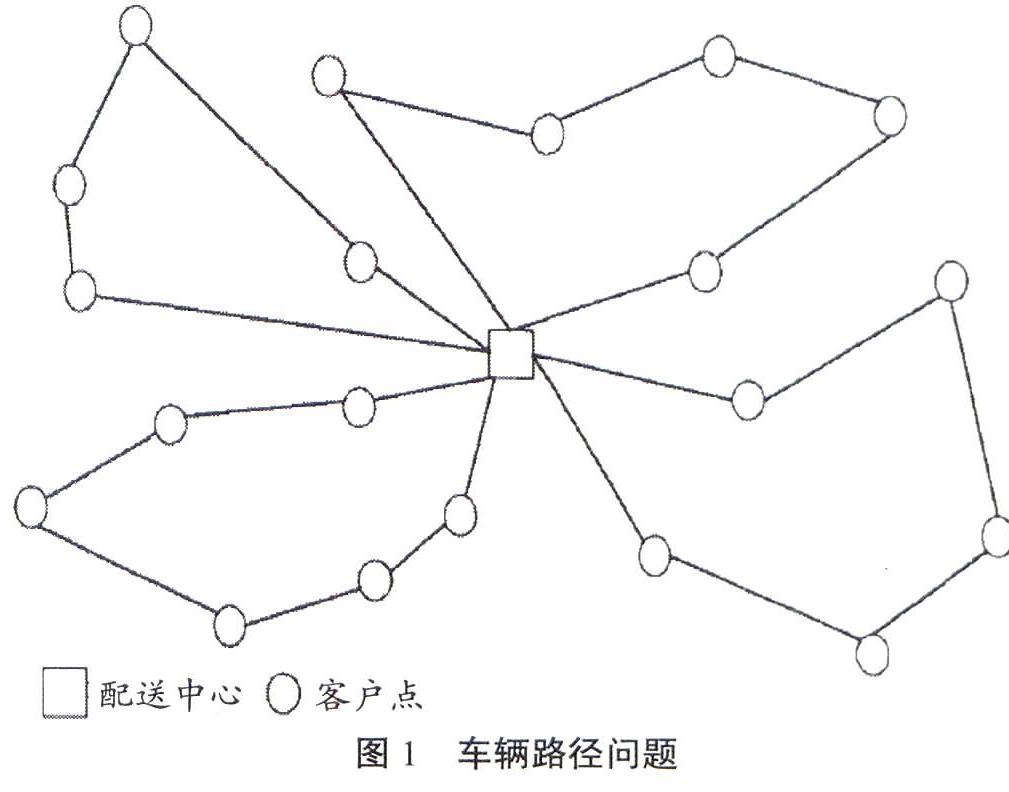
径[1-4]。TSP问题描述起来简单,但解决却很复杂,在实际问题中,很多旅游路线并非完整的旅行商问题,游客去多个景区游玩并不是组成一个完整的闭回路,而是每次出行均有时间限制,分几次旅行,每次出行去计划的某些景区之中的某几个之后再回到原点,并且每个景区的开放时间是固定的,此问题即演变成了带有时间窗车辆路径问题(VRP)[5-6]。如图1所示,图中正中间点表示车辆起始点(车场或配送中心),每个闭合圈内的点表示需要到达的客户点,两点之间则表示路段,每条路线对应着一个费用,通常表示其距离或行驶时间。
为解决该类旅游路线规划问题,为此类游客提供更好的路径体验,本文建立数学模型,并用蚁群算法求解模型,通过计算机编程仿真得到最优旅游路线。
1 模型的建立
1.1 问题描述
式(1)为目标函数,及要求旅游时时间最短,约束式(2)、式(3)表示每个景区只游览一次,约束式(4)旅游爱好者进入景区i,也定会离开景区i,约束式(5)表示每次旅行的最大限制时间,每次出游时间不能超过限制天数,约束式(6)为景区节点时间窗约束。
2 蚁群算法求解模型
蚁群算法(Ant Colony Optimization, ACO),是一种典型的仿生物算法,20世纪M. Dorigo等学者从蚂蚁觅食行为的研究中受到启发,进而提出的一种优化算法[7-8]。当一只蚂蚁发现一条通往食物所在地的路径时即会释放出一种“信息素”,并根据信息素浓度来决定下一刻的移动方向,初始时刻各条路径信息素浓度是一样的;当蚂蚁沿着这条路到达终点后便会沿着原路返回;如此,短路径上的蚂蚁经历过的次数就越多,信息素浓度也就大,于是吸引更多蚂蚁,信息素继续升高,如此循环,最后找到最佳路径。蚁群算法便捷准确,可以利用该算法来求解各种复杂的VRP问题。求解过程如下:
step1:设置初始参数;
step2:给第k只蚂蚁随机选择起始点i,并把起始点i放入第k只蚂蚁搜索禁忌表中,如果i为西安市,则将西安市删去;
step3:求最大转移概率maxp,得到下一个点j;
step4:考察和j连接后的线路上旅游次数sumg,若sumg≤Q(Q为游客每次出游最长限制时间),则转下一步,否则,转step6;
step5:计算s,若s满足时间窗要求,把点j放入tabu中,计算i点到j点路径所用时间,转step3,否则转下一步;
step6:统计旅游次数,根据次数判断allowed表,如果allowed表空,那么转下一步;并转step3,继续搜索下一个点;
step7:重新计算各边信息素以及信息素的增量;
step8:搜索k只蚂蚁最短时间路径,更新蚂蚁每条路线信息素,若有k只蚂蚁均巡游一遍,则更新k只蚂蚁搜索过路径的信息素,否则,更新该次循环最优路径;
step9:若算法循环NC_max后停止,则计算NC_max后最短路径长度和最短路径,最少费用和最少费用路径,否则转step2。
从以上步骤可知,在整个循环中,蚂蚁的起点不都是原点,而是随机选择的,这样做更检验算法的正确性,选择不同的起始点更有利于找到更好解。当该蚂蚁不满足以上约束条件,需要在剩余的点中寻找新的起点(用时最短的点),这样在最大程度上提高了算法的效率。
3 仿真结果分析
假设该旅游爱好者每年外出旅游时间不超过30天,每年外出旅游次数不超过4次,每次旅游时间不超过15天;根据个人爱好确定了每个5A级景区最少的游览时间。景区开放时间统一规定为8:00至18:00。经过建模求解仿真如图2所示、详细路径如表1所示。
根据仿真结果求得最短时间为10.5年,即在本题目约束条件下,该旅游爱好者自驾游玩全国201个5A级风景区

