副车架系统边界约束对计算模态分析精度的影响研究

陈达亮李洪亮,顾灿松王海洋任　斌

（1.中国汽车技术研究中心，天津300300；2.河北工业大学，天津300130）



副车架系统边界约束对计算模态分析精度的影响研究

陈达亮1李洪亮1,2顾灿松1王海洋1任斌2

（1.中国汽车技术研究中心，天津300300；2.河北工业大学，天津300130）

【摘要】针对某车型“刚性”副车架系统建立有限元模型，以约束处理方式为设计变量，以0～200 Hz范围内的约束模态频率计算值与试验值的误差作为评价指标进行正交试验设计，分析得到不同约束处理方式对副车架约束模态分析精度的影响规律。结果表明：副车架与车身连接点处车身局部刚度对模态分布的影响较大，悬架摆臂次之，衬套动刚度对模态分布的影响相对较弱；基于正交试验遴选出的最佳边界约束处理方式，可得约束模态频率计算值与试验结果的相对误差为0.45％，达到了理想精度。

1　副车架系统及其边界约束

副车架连接车身和悬架，在一定程度上起到隔振降噪的作用。图1为某型汽车的“刚性”副车架系统，其特点是副车架结构通过螺栓“刚性”地固定于车身。副车架系统主要受2种激励，即来自不平路面的激励和来自发动机的激励。

一般情况下2种激励都会通过副车架系统传至车身，严重时会削弱车辆的乘坐舒适性。因此，副车架系统动态特性直接影响汽车NVH性能。工程上常用的研究方法是通过模态分析来探究副车架系统的动态特性。

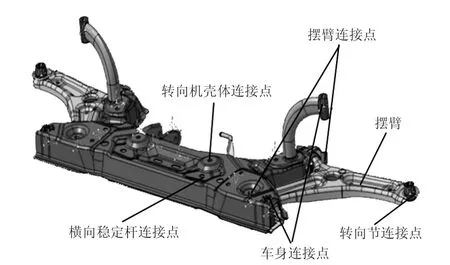
图1　某型汽车“刚性”副车架系统

计算机辅助工程（Computer Aided Engineering，CAE）具有高效率、低成本等优点，因而成为研究结构动态特性的常用方法，在车架及副车架方面已有相关研究成果［1～5］。有限元建模过程中对约束边界的不同处理方式会得到不同精度的仿真结果，文献［6］通过有限元法计算某车型前副车架在自由状态、忽略衬套连接的刚性约束状态以及安装状态下（包含衬套连接）的模态并将计算值与试验值进行对比，结果表明前副车架与车身搭接件安装处的刚度是决定前副车架振动频率高低的主要原因。但单一副车架模型没有考虑到下摆臂对副车架系统的影响，这会给计算结果带来误差，并且计算副车架系统安装状态下的约束模态时需要依托整车模型建模，这不仅增大了工作量而且降低了计算效率。文献［7］利用AD⁃AMS软件分析了副车架-橡胶衬套-车身12自由度刚柔耦合振动系统的特性，结果表明副车架与车身连接处的衬套刚度应相互匹配才能达到较好的效果，这说明当副车架的约束边界涉及弹性部件时，弹性部件对激励响应的滞后程度也会影响系统的振动传递特性。因此，对副车架约束边界条件进行细致分析具有重要的意义。

本文针对图1所示的副车架系统采用有限元法建立模型，探究不同的边界约束处理方式对副车架系统有限元模态分析精度的影响。即以边界约束的处理方式为设计变量，以0～200 Hz（低频）内副车架系统计算约束模态频率与试验值的误差作为评价指标进行试验设计，分析不同的边界约束处理方式与模态分析精度的关系，以期遴选出最佳的边界约束处理方式。

2　边界约束处理与有限元建模

2.1副车架系统的约束边界

如图1所示，副车架结构通过螺栓固定于车身，通过橡胶衬套与横向稳定杆、转向机壳体以及悬架摆臂连接，摆臂另一端通过球铰与转向节连接。副车架结构及其约束边界构成了模态分析的对象系统。

悬架下摆臂一端与副车架通过橡胶衬套连接，其刚度较弱，使得被连接部件处于相对浮动状态；下摆臂另一端则通过球铰与转向节连接，具有完全的转动自由度。模型中，对悬架下摆臂的处理方式有如下2种。

a.由于悬架摆臂与副车架之间约束较弱，因此将摆臂舍去，使副车架在与摆臂连接点位置处于自由状态；

b.将悬架摆臂视为副车架系统的一部分，摆臂与转向节的球铰连接因而视为副车架系统的约束边界。

副车架通过橡胶衬套与横向稳定杆、转向机壳体连接，而横向稳定杆和转向机壳体的刚度远大于衬套刚度，并且它们与车身之间为刚性连接，因此，模型中将横向稳定杆和转向机壳体视为车身的一部分。

所谓“刚性”副车架，是其与车身连接处不设置弹性减振与缓冲元件，因而具有相对较大的局部刚度。针对这一特点，模型中对副车架与车身连接处约束的处理有2种方式：

a.将副车架与车身视为刚性连接；

b.用衬套模拟副车架与车身连接，衬套刚度赋值为副车架与车身连接处的车身局部刚度。

橡胶衬套刚度特性主要分为静刚度和动刚度，对衬套刚度的处理，此处提供2种方式：

a.只考虑衬套静刚度，这种处理方式的优点是数据测量简单且在软件中赋值方便，不足之处是没有考虑衬套的动态特性；

b.考虑衬套动刚度，这种处理方式的优点是可使模型更符合实际情况，缺点是数据测量比较困难且部分有限元分析软件不支持橡胶衬套的动刚度曲线输入。

综上所述，处理副车架系统约束边界主要从3个角度出发：是否将麦弗逊悬架下摆臂视为副车架系统的一部分；是否引入车身局部刚度以模拟副车架系统与车身的连接；是否考虑橡胶衬套动刚度。

2.2基础参数获取与有限元建模

根据上述对约束边界的讨论，确定需要通过测量手段获取的建模基础参数主要包括橡胶衬套静刚度、动刚度和副车架与车身连接点处的局部刚度。分别采用MTS831.50弹性体试验台和MTS832衬套试验台测量橡胶衬套静刚度和动刚度，并以动刚度曲线在0～200 Hz范围内的RMS值来近似代替动刚度。相应的测量和计算结果如表1和表2所示，其中各坐标皆处于整车坐标系下。另一方面，通过试验测试副车架与车身连接处的局部刚度，结果如表3所示。限于测试条件，连接部位的角刚度无法测量，因此在模型中带入经验值。

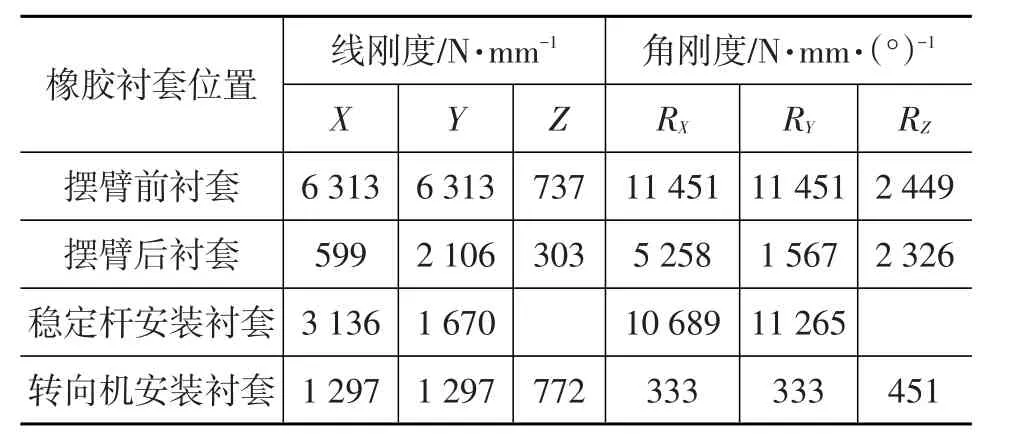
表1　橡胶衬套静刚度

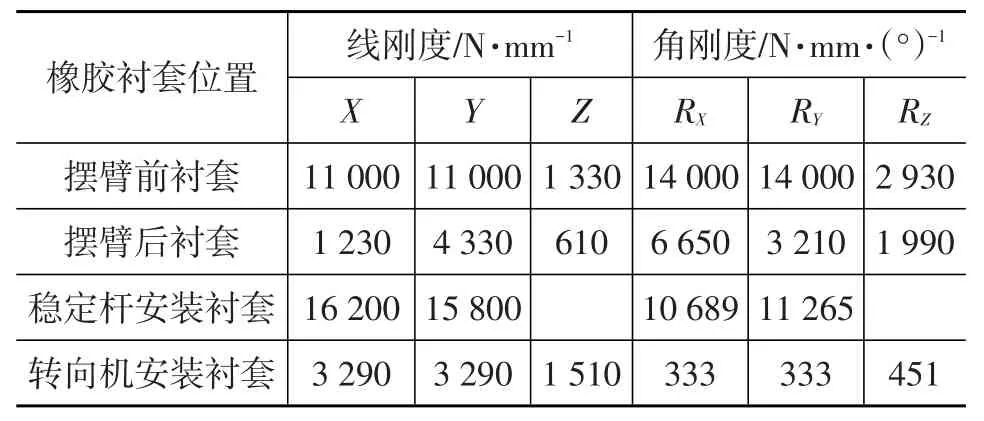
表2　橡胶衬套动刚度RMS值

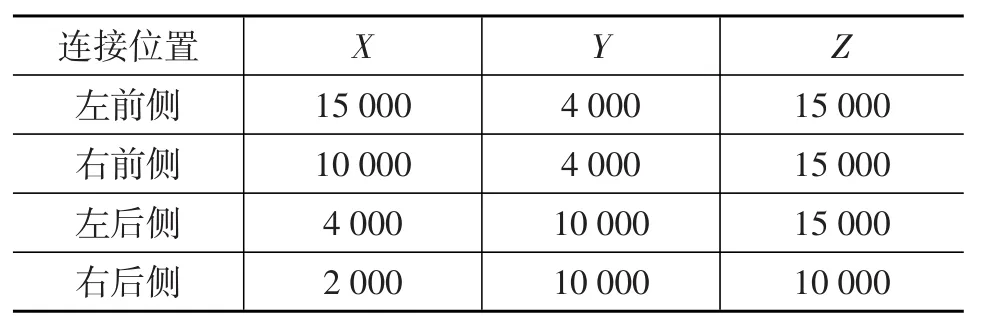
表3　车身安装点处车身钢板局部动刚度　N/mm

在划分有限元网格前，对几何模型进行特征清理并删除对模态影响较小的部分圆角和小孔特征。对几何模型抽取中面并采用四边形壳单元划分网格，经多次调试对比最终确定网格大小为8 mm。该副车架材料为45#钢。所建立有限元模型的单元数为12 891，节点数为16 575，并可灵活设置不同的边界约束，如图2所示。

图2　副车架有限元模型

3　边界约束处理方式的试验设计

3.1基本思想

正交试验设计方法是20世纪50年代至70年代之间由日本统计学家田口玄一提出的一种试验设计方法。应用这一方法研究变量对试验结果的影响时，可以在不影响分析精度的前提下显著减少试验次数［8～10］。这里，以副车架系统的边界约束处理方式作为试验的设计变量，以0～200 Hz低频范围内的有限元计算模态频率误差作为评价指标，进行边界约束处理方式的试验设计。此处，计算模态频率的误差定义为其与相应的试验模态分析结果之间的差异。因此，首先要对副车架系统进行相应的模态测试。

3.2副车架约束模态试验

在实车安装状态下，通过测试获取副车架系统试验模态分析结果。传感器布置如图3所示，测试采用单输入多输出的方式进行。测试结果表明，在0～200 Hz频率范围内，副车架系统只有1阶模态，模态频率点为175.9 Hz，模态振型如图4所示。

图3　副车架系统约束模态试验示意

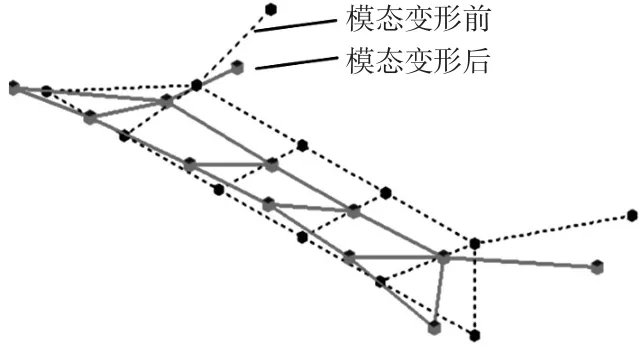
图4　副车架系统试验约束模态振型

3.3试验设计结果分析

针对2.1节提出的约束边界的3种处理方式，在试验设计中将其视为影响建模精度的3种因素并对每种因素设置2个水平：对于衬套刚度，数字1表示考虑静刚度，数字2表示考虑动刚度，即模型中带入橡胶衬套动刚度在0～200 Hz内的RMS值；对于摆臂，数字1表示在模型中不考虑副车架与悬架摆臂的连接关系，即副车架与摆臂连接点位置处于自由状态，数字2表示将摆臂视为副车架系统的一部分，并将摆臂与转向节的球铰连接视为副车架系统的约束边界；对于车身安装点刚度，数字1表示将车身视为纯刚体，即副车架与车身连接处钢板的刚度为无穷大，数字2表示考虑车身安装点处车身钢板的局部刚度，并在模型中用橡胶衬套模拟副车架与车身的连接关系。由此进行试验设计。

在所有约束条件下均可将车身视为与大地固定的刚体，在有限元模型中分别添加第1、2、3、4组约束条件，计算约束模态并与试验值对比，以模态频率误差作为评价指标，计算分析结果如表4和表5所示。

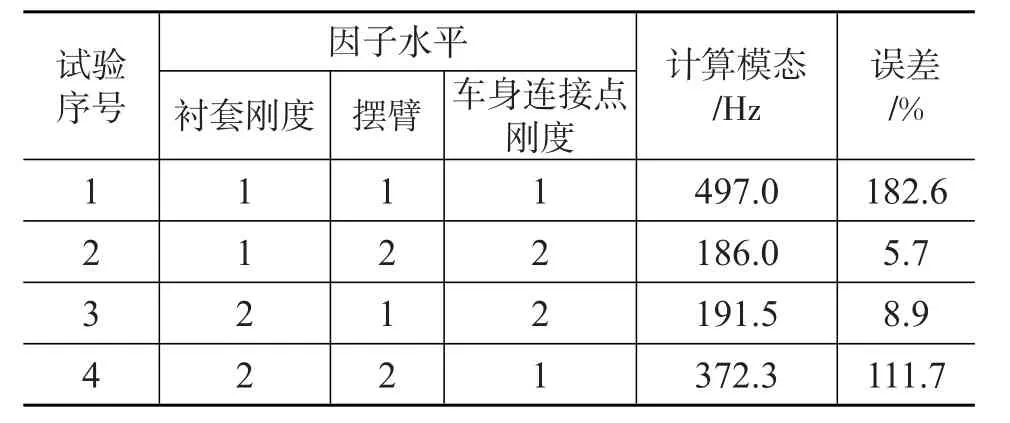
表4　正交试验计算结果

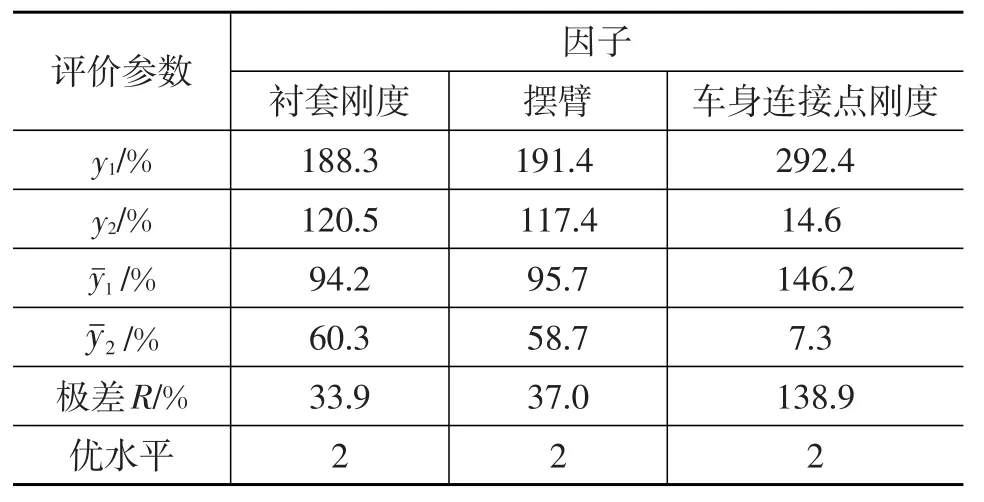
表5　正交试验分析结果

表5中，yk为某因素k（k=1/2）水平对应的试验指标（即模态频率误差）之和；为yk的平均值；R为某因素的极差，即该因素不同水平对应平均值中最大值与最小值的差值。应用极差分析法可以判断每个因素对指标影响程度的大小。从表5中的极差R可以看出，副车架与车身连接关系的处理对建模精度的影响相对最大，橡胶衬套是否考虑动刚度特性对建模精度的影响相对最小，而摆臂的处理方式对建模精度的影响介于两者之间。

3.4试验设计结果验证

根据正交试验结果选出约束边界处理方法的最优组合如表5中“优水平”一栏所示：考虑衬套动刚度特性、将摆臂引入副车架系统以及将副车架与车身连接视为柔性。依据这一组合修改有限元模型约束边界后重新计算约束模态结果如图5所示。

图5　计算模态振型

依据正交试验结果对副车架约束边界进行修改后，有限元模型计算约束模态频率为176.7 Hz，试验值为175.9 Hz，误差为0.45％。相比于正交试验中其它约束边界处理方式组合，经正交试验优化遴选出的约束边界处理方式在模型中的计算约束模态频率与试验值误差最小。

另一方面，对比图5和图4中的副车架系统模态振型，可以发现两者具有很高的相似性：它们均为副车架绕Y轴（整车坐标系）的俯仰振动，没有沿Y轴的平动。

综上所述，经正交试验选出的边界约束处理方式应用到有限元模型中后，计算约束模态与试验约束模态存在较好的吻合。

4　结束语

a.“刚性”副车架系统与车身连接点处局部刚度对有限元模态分析精度的影响相对较大，摆臂次之，橡胶衬套刚度对模型精度的影响相对前两者要弱。因此，在模型中需要细致处理副车架与车身连接点处的约束关系，使连接点处的局部刚度特性能够在模型中正确体现。

b.经试验设计分析遴选出的边界约束处理方式显著提高了模型分析计算的精度，表明了该方法的有效性，并可为类似问题的研究提供参考。

参考文献

1郑灏.汽车前副车架有限元分析及优化：［学位论文］.武汉：武汉理工大学，2012.

2刘宝生.基于有限元法的摩托车车架振动响应与可靠性分析：［学位论文］.天津：天津大学，2010.

3郑松林，赵德彪，冯金芝，等.基于强度与模态灵敏度分析的轿车前副车架轻量化设计.机械设计，2012，29（2）：92～96.

4王锐，苏小平.汽车副车架强度模态分析及结构优化.机械设计与制造，2015（4）：152～154.

5王晓明，孟令超，沈勇，等.装载机后车架动态特性分析及结构改进.建筑机械，2014（8）：63～70.

6孙风蔚，徐昊，陈杰龙，等.某车前副车架模态分析与改进.汽车工程学报，2012，2（4）：303～306.

7赵帅.轿车副车架隔振性能的动态建模研究：［学位论文］.长春：吉林大学，2014.

8姜立标，侯文超，谷方德.基于正交试验的汽车稳态回转性能仿真.北京航空航天大学学报，2011，37（8）：968～972.

9张晗，过学迅，杨波，等.基于正交试验的载货汽车转向回正性仿真试验研究.机械设计与制造，2013（5）：137～139.

10廖鸿胡，赵云飞，成艾国，等.基于正交试验的汽车滑移门平顺性优化研究.机电工程，2010，27（12）：49～52.

（责任编辑斛畔）

修改稿收到日期为2015年8月19日。

主题词:副车架系统有限元法边界约束模态分布正交试验设计

The Effect of Subframe System Boundary Constraints on the Accuracy of Computational Modal Analysis

Chen Daliang1, Li Hongliang1,2, Gu Cansong1, Wang Haiyang1, Renbin2
（1.China Automotive Technology and Research Center, Tianjin 300300; 2. Hebei University of Technology, Tianjin 300130）

【Abstract】FE model of a vehicle "rigid" subframe system is established, the influence law of different constraint processing modes on the accuracy of subframe constraint modal analysis is obtained through analysis with the constraint processing mode as design variable, and the error between constraint computational modal frequency and experimental value in the range of 0～200 Hz as evaluation criteria for the orthogonal experimental design. The results show that the local stiffness of the joining part between subframe and body is the most important factor to affect modal distribution, followed by the suspension swing arm, whereas the sleeve dynamic stiffness affects modal distribution slightly; the optimal boundary constraint processing mode is selected based on orthogonal experiment, and it is concluded that the relative error of the computational modal frequency compared with the experimental one is 0.45％, thus a relative ideal accuracy is obtained.

Key words:Subframe system, Finite element method, Boundary constraint, Modal distrubution, Orthogonal experimental design

中图分类号:U463.83

文献标识码:A

文章编号:1000-3703（2016）04-0027-04