基于遥感的海南岛橡胶林零平面位移和粗糙度估算
刘少军 易雪 张京红 蔡大鑫 田光辉 李伟光


摘 要 在橡胶风害评估中,橡胶林零平面位移和粗糙度是建立定量评估模型的重要动力学参数。以MODIS遥感数据为信息源,计算橡胶林的叶面积指数,并利用形态学Raupach方法,估算橡胶林归一化零平面位移和粗糙度。该方法充分发挥了遥感大面积获取数据的优势,同时解决了传统气象学方法获取橡胶林零平面位移和粗糙度需要大量长期的野外观测资料的限制。结果表明:橡胶林叶面积指数与归一化零平面位移和粗糙度分别存在正相关和负相关;估算结果精度能满足橡胶风害评估模型参数的需求。研究结果可为开展大范围内橡胶林风害评估提供技术支撑。
关键词 橡胶林;零平面位移;粗糙度;海南岛
中图分类号 P49 文献标识码 A
Abstract Zero-plane displacement and roughness length of rubber are crucial parameters in the typhoon impact assessment model on rubber plant. Leaf area index was derived based on the MODIS remote sensing data. Zero-plane displacement and roughness length of rubber were derived by the morphology model. This method not only made full use of the advantage of remote sensing, but also solved the traditional meteorology method to get zero-plane displacement and roughness depending on a long-term field observation data. The results showed that leaf area indices were positively and negatively correlated with d/h and z0/h. The accuracy of result could meet the need of rubber wind damage assessment model parameters. The results provided technical support for carrying out large scale rubber wind damage assessment.
Key words Rubber plant;Zero-Plane Displacement;Roughness Length;Hainan Island
doi 10.3969/j.issn.1000-2561.2016.10.029
零平面位移和粗糙度是描述下垫面空气动力学特征的重要参数[1]。零平面位移为下垫面开始吸收动量的高度,地表粗糙度是下垫面风速为零的高度[2],但在不同天气背景下, 零平面位移和粗糙度长度并不是常数[3]。在海南橡胶林台风灾害动力学评估模型中,橡胶树断、倒条件的判识,必须解决大范围、不同季节、不同地形条件下橡胶林零平面位移和粗糙度。由于早期的研究对零平面位移和粗糙度的理解不确切,一般通过冠层高度和叶面积指数等分别建立零平面位移和粗糙度的经验公式进行估算[4-7]。零平面位移和粗糙度是风速和大气层结的函数,而不仅仅是由冠层几何高度来确定[3,8]。目前,零平面位移和粗糙度的计算一般存在气象学和形态学两种方法[9]。气象学方法常采用三维超声风温仪,观测多层的风速观测资料,然后利用风速廓线公式通过迭代求解[1,10]。如张学仕等[1]利用应用温度方差方法计算了江苏句容下蜀次生栎林空气动力学参数;钟中等[3]根据空气质量守恒原理, 对长白山天然阔叶红松林冠层空气动力学参数进行了数值计算;赵晓松等[10]利用廓线法中的牛顿迭代法计算了长白山阔叶红松林的零平面位移和粗糙度;Lo[11]根据冠层上下多层风、温观测资料计算高大森林冠层零平面位移和粗糙度的方法。而形体学方法主要是采用粗糙元高度、粗糙元顶部面积、粗糙元迎风面积等计算零平面位移和粗糙度[12]。如杨阿强等[9]采用粗糙元形态学方法,计算中国东部不同季节空气动力学零平面位移和粗糙度;Macdonald等[13]根据粗糙元迎风面积和顶部面积的方法计算零平面位移和粗糙度。
形态学方法比气象学方法更具有优势。气象学方法物理意义更为确切,不同参数具有不同的物理含义,但计算过程中需要在稳定中性大气条件下准确测量气象数据,推导橡胶林零平面位移和粗糙度对于大范围长时间序列的计算需要大量长期的野外观测,成本较高;而形态学方法是根据物理基础经过简化综合经验系数得到的,精度需要不断提高,但其方法可以采用遥感数据作为数据源,而且可以进行大范围内参数的反演[9]。目前,关于采用遥感和形态学方法估算橡胶林零平面位移和粗糙度的研究未见报道。因此,本研究采用遥感数据源,尝试利用形态学模型的方法,估算海南岛橡胶林零平面位移和粗糙度,为快速大范围获取橡胶林动力参数提供了新的技术途径。
1 材料与方法
1.1 材料
海南岛MODIS遥感数据、TM遥感数据提取海南天然橡胶空间分布图(具体方法参考文献[14-15])、2011年海南天然橡胶普查数据、橡胶生产分布以农场为单位进行统计,数据来源于文献[16]。省界和县界行政区划图来源于国家基础地理信息网站提供的1 ∶ 400万基础地理信息数据(http://ngcc.sbsm.gov.cn/)。
1.2 方法
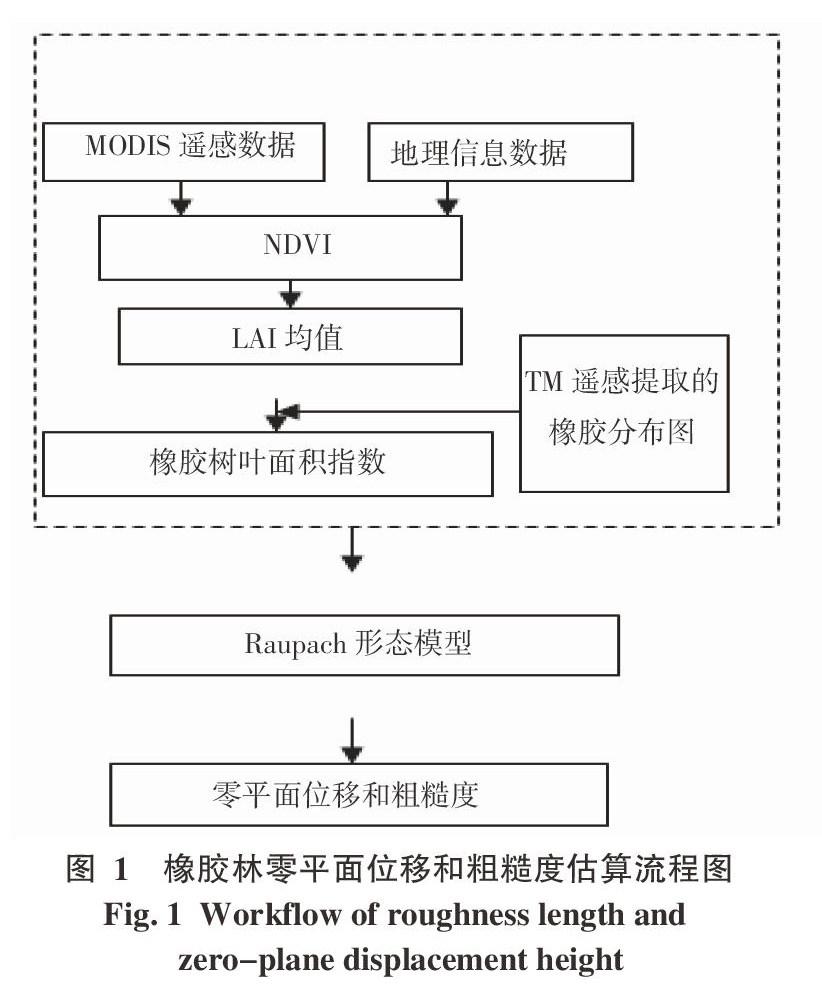
在形态学方法中,一般认为Raupach[17]方法精度较高[18],因此选择Raupach方法进行海南岛橡胶林零平面位移和粗糙度估算。通过提取橡胶林叶面积指数、相关参数计算,代入Raupach 的形态学模型,计算海南岛橡胶林零平面位移和粗糙度。具体技术流程见图1。
1.2.1 橡胶叶面积指数提取 叶面积指数(Leaf Area Index,LAI)又叫叶面积系数,是指单位土地面积上植物叶片总面积占土地面积的倍数。即:叶面积指数=叶片总面积/土地面积。叶面积指数(LAI)作为植被冠层的重要结构参数之一,是许多生态系统生产力模型和全球气候、水文、生物地球化学和生态学模型的关键输入参数。叶面积指数的计算方法有:直接方法(叶面积的测定、描形称重法、仪器测定法);间接方法(点接触法、消光系数法、经验公式法、遥感方法)。本文通过橡胶林叶面积指数(LAI)和归一化植被指数(NDVI)统计关系,计算得到如下回归方程,进行天然橡胶叶面积指数的反演。
LAI=7.82NDVI+0.781 (1)
其中,归一化植被指数的计算公式如下:
式中,NDVI表示归一化植被指数,Rnir表示近红外波段反照率,Rred表示可见光波段(红光)反照率。
1.2.2 零平面位移和粗糙度估算 Raupach的形态学公式表示如下[17]:
d为零平面位移,ZO为粗糙度,h为粗糙元高度,λ为单位地面粗糙元迎风面积,ψh为粗糙层影响函数,b为冠层宽度,Cd为经验系数。β为粗糙元阻力系数与地表阻力系数之比,γ为距地面高度z 处的水平风速与摩擦速度之比。其中单位地面粗糙元迎风面积λ可以为:
A表示为单位面积上植被对风的阻挡面积,值与叶面积指数很接近[19],因此采用遥感反演的叶面积指数LAI表示单位面积上植被对风的阻挡面积。
模型中其他参数参考相关文献获取[4-8,10-13]。
2 结果与分析
本次研究选择了2015年3月中旬云量相对较少的MODIS遥感数据,并结合海南岛橡胶分布[14-16],分别提取了海南岛橡胶林的叶面积指数、归一化零平面位移、归一化粗糙度分布图。
结果显示:海南岛橡胶林的叶面积指数在1.0~8.6之间,高值区分布在海南岛的中部和东南部区域,低值区域分布在海南岛的北部和西部区域(图2),遥感叶面积指数的差异体现了此时橡胶冠层物候的差异。其主要原因是该时段海南岛橡胶普遍进入第一蓬叶展叶期,但由于不同区域的温度、降水、光照、风速等的差异,对此时橡胶叶的生长有着不同的影响,一般以东南和南部地区最早出现,最后是西北部和中部地区[20]。
海南橡胶林归一化零平面位移在0.5~0.82之间,归一化零平面位移最大值为0.82,最小值为0.5,平均值为0.75,标准差0.046。高值区分布在海南岛的中部和东南部区域,低值区域分布在海南岛的北部和西部区域(图3)。由上可知,橡胶林的归一化平均零平面位移与叶面积指数变化趋势相一致,高值和低值区分布基本一致。通过ArcGIS软件的Spatial analyst tools-Multivariate-Band collection statistics功能模块,计算两者的相关性为0.85。
海南橡胶林归一化粗糙度在0.056~0.10之间,归一化粗糙度最大值为0.10,最小值为0.056,平均值为0.073,标准差0.012。低值区分布在海南岛的中部区域,高值区域分布在海南岛的北部和西南部区域(图4)。归一化粗糙度的变化趋势与橡胶林叶面积指数高值和低值区的分布相反。通过ArcGIS软件计算两者的相关性为-0.84。其主要原因可能是当橡胶林叶面积指数高值时,橡胶树叶片相对繁茂,使气流从作物顶部通过,从而减小了气流同叶片的摩擦降低了空气动力学粗糙度。
3 讨论与结论
本文在借鉴前人研究方法的基础上,结合资料可获得性及满足大范围获取橡胶林零平面位移和粗糙度的需求,尝试利用MODIS遥感数据和Raupach的形态学模型,采用的计算方法是建立在严格的理论推导基础上,同时兼顾经济性原则,希望突破以往有关零平面位移和粗糙度取值的经验性约束,为橡胶林动力学风害评估模型提供动力参数。
橡胶林零平面位移和粗糙度实际上是随大气稳定情况发生改变的,可能同一天都会相差很大,不同大气层结状态,零平面位移和粗糙度均会有所差异,同时橡胶林平面位移和粗糙度随季节会发生变化。遥感反演的海南橡胶林d/h和z0/h与橡胶林叶面积指数分别存在正相关和负相关的关系。这与Shaw等[21]、赵晓松等[10]利用气象观测塔实测数据计算的规律一致。
本研究由于缺乏与遥感数据相对应时间段的通量塔观测资料与之进行对比验证,导致无法进行遥感反演精度的直接验证。但橡胶树属于阔叶林,相关参数的验证仅与前人[9-10,22-24]的森林的结果进行对比分析,根据2015年3月15日MODIS数据反演的海南岛橡胶林归一化零平面位移和粗糙度均在同一量级范围内,反演结果整体上反映了橡胶林归一化零平面位移和粗糙度在空间分布的差异,能满足橡胶林风害模型的参数要求,但具体的误差仍需要与后期建立橡胶林观测数据进行对比分析,不断改进Raupach的形态学模型相关参数,以提高遥感反演橡胶林零平面位移和粗糙度的精度。
由于本文仅停留在利用Raupach方法,探索性地估算橡胶林零平面位移和粗糙度,而且相关参数主要参考了经验值;同时由于橡胶林的面积的来源主要参考文献[14-16]的成果,没能及时更新,难免存在误差和不足。
参考文献
[1] 张学仕, 蒋 琰, 薛建辉, 等.江苏句容下蜀次生栎林的空气动力学参数研究[J]. 南京林业大学学报:自然科学版, 2010, 34(6): 61-65.
[2] 蔡 福, 周广胜, 明惠青, 等. 玉米农田空气动力学参数动态及其与影响因子的关系[J]. 生态学报, 2013, 33(17): 5 339-5 352.
[3]钟 中, 韩士杰. 长白山阔叶红松林冠层空气动力学参数的计算[J]. 南京大学学报(自然科学), 2002, 38(4): 565-571.
[4] Szeicz G, Endrodi G, Tajchman S. Aerodynamic and surface factors in evaporation[J]. Water Resources Research, 1969, 5(2): 380-394 .
[5] Stanhill G. A Simple instrument for field measurement of turbulent diffusion flux[J]. Journal of Applied Meteorology, 1969(8): 509-513 .
[6] Zoumakis N M. Determination of the mean wind speed and momentum diffusivity profiles above tall vegetation and forest canopies using a mass conservation assumption[J]. Journal of Applied Meteorology, 1994, 33: 295-302.
[7] Raupach M R. Simplified expressions forvegetation roughness length and zeroplane displacement as functions of canopy height and area index[J]. Boundary-Layer Meteorology, 1994, 71(1-2): 211-216.
[8] Lesnik G E.Estimation of displacement layer thickness and roughness parameter from measurements above a forest[J]. Izvestiya Atmospheric And Oceanic Physics, 1973, 9(1): 88-90. [9] 杨阿强, 孙国清, 卢立新, 等.基于MODIS资料的中国东部时间序列空气动力学粗糙度和零平面位移高度估算[J]. 气象科学, 2011, 31(4): 516-524.
[10] 赵晓松, 关德新, 吴家兵, 等.长白山阔叶红松林的零平面位移和粗糙度[J]. 生态学杂志, 2004, 23(5): 84-88.
[11] Lo A K. Determination of zero-plane displacement and roughness length of a forest canopy using profiles of limited height[J]. Boundary-Layer Meteorology, 1995, 75: 81-402.
[12] RaupachM R, Antonia R A, Rajagopalan S. Rough-wall turbulent boundary layers[J]. Applied Mechanics Reviews, 1991, 44(1): 1-25.
[13] Macdonald R W, Griffiths R F, Hall D J. An improved method for estimation of surface roughness of obstacle arrays[J]. Atmospheric Environment, 1998, 32(11): 1 857-1 864.
[14] 张京红, 陶忠良, 刘少军, 等.基于TM影像的海南岛橡胶种植面积信息提取[J]. 2010, 31(4): 661-665.
[15]刘少军, 张京红, 何政伟. 基于面向对象的橡胶分布面积估算研究[J]. 广东农业科学, 2010, 37(1): 168-170.
[16] 唐群锋, 郭澎涛, 刘志崴, 等. 基于FMT-AHP的海南农垦花岗岩类多雨区橡胶园地力评价[J]. 生态学报, 2014, 34(15): 4 435-4 445.
[17] Jasinski M F, Borak J, Crago R. Bulk surface momentum parameters for satellite-derived vegetation elds[J]. Agricultural and Forest Meteorology, 2005, 133: 55-68.
[18] Grimmond C S B, Oke T R.Aerodynamic properties of urban areas derived from analysis of surface form[J]. Journal of Applied Meteorology, 1999, 38: 1 262-1 292.
[19] ZENG Xubin, Shaikh Muhammad, Dai Yongjiu, et al. Coupling of the common land model to the NCAR community climate model[J]. Journal of Climate, 2001, 15: 1 832-1 854.
[20] 陈小敏, 陈汇林, 李伟光, 等. 海南岛天然橡胶林春季物候期的遥感监测[J]. 中国农业气象, 2016, 37(1): 111-116.
[21] Shaw R H, Pereira A R. Aerodynamic roughness of a plant canopy: a numerical experiment[J]. Agricultural Meteorology, 1982, 26: 51-65.
[22] 连士华. 橡胶树风害成因间题的探讨[J]. 热带作物学报, 1984, 5(1): 59-72.
[23] 刘和平, 刘树华, 朱廷曜, 等.森林冠层空气动力学参数的确定[J]. 北京大学学报(自然科学版), 1997, 33(4): 522-528.
[24] Borak Jordan S, Jasinski Michael F, Crago Richard D. Time seriesvegetation aerodynamic roughness fields estimated from MODISobservations[J]. Agricultural and Forest Meteorology, 2005, 135: 252-268.

