基于SMSA算法的网壳结构优化设计

高占远

【摘要】提出了应用SMSA（Simulated Simplex-annealing，单纯形模拟退火）算法对网壳结构进行优化设计，并对算法中参数的选择进行了探讨，算例分析表明了单纯形模拟退火算法应用在网壳结构优化中的可行性和有效性。

【关键词】单纯形模拟退火；优化；网壳结构

[文章编号]1619-2737（2016）01-30-508

1. 引言

单纯形（SM）算法最早由Nelder和Mead于1965年提出并应用在最优化问题中，后来英国剑桥大学的Press给出了算法的完整过程和标准化程序。[1]模拟退火算法（SA）最初由Metropolis于1953年首先在物质状态方程求解时提出，该方法是按自然法则计算的重要分支，它将组合优化问题与统计力学中的热平衡问题相类比，从而发展起来的全局优化方法。[1]SMSA算法最早是用来解决NLP问题，针对模拟退火算法存在收敛慢、费机时较多的缺陷，将单纯形法和模拟退火算法有机地结合起来，形成一种新的改进型的优化算法——单纯形模拟退火算法，以加快收敛速度、提高解的质量。随着模拟退火算法的发展，SMSA算法也不断得到发展，使它可以应用到更多的领域。

1. SMSA算法

单纯形法是一种直接、快速地搜索极小值的方法。当目标函数具有多个极小值时，由于初值选取不同会得到不同的结果，并且还不一定是目标函数的极小值，而只是一个局部极小值。模拟退火法采用的是随机搜索方法，它能跳出局部极小值的陷阱、最终得到全局最小值，但同时在搜索过程中作了很多无用功，浪费时间，效率较低。因此，可以考虑结合两种方法的优点，联合起来求解优化问题。

单纯形模拟退火算法的基本思想是，对任一给定初始解X0，首先用单纯形法快速求得一个极小值点，然后改用模拟退火法随机搜索，跳离该局部极小值，一但找到一个比该极小值点更小的点，就立即以该点为初始值调用单纯形法直接搜索该点附近的另一个极小值点，如此交叉进行，直到终止条件，算法结束，得到的结果必为目标函数的全局最小值。

单纯形模拟退火算法思路清晰，方法简便，效率高，适合于求解多变量且具有多个极值点的优化问题，下面说明该方法的实现步骤：

2. 网壳结构优化的数学模型

网壳结构优化的设计变量为杆件的截面积，目标函数为结构的总体重量，约束条件为杆件的应力约束、节点的位移约束。优化数学模型如下：

3. 模拟退火算法中参数的实现

3.1初始温度的选取方法。

本文是采用数值计算估计方法给出一个接近1的数N和初始温度T，按以下算法进行计算：

3.3降温准则。

模拟退火算法成功与否的一个关键因素，就是选择一个合理的降温准则，因为降温准则跟解的产生机制和终止准则有很大关系。本文采用的是杨若黎[4]等提出的一种降温更新函数的启发式准则：

3.5终止准则。模拟退火算法从初始温度开始，通过在每一温度的迭代和温度的下降，最后达到终止规则而停止。本文采用以下几种终止准则同时控制：

（1）温度：一般采用温度接近于0时一个很小值作为终止条件，既要保证exp（-Δf/TC）→0，算法收敛到最优解。

（2）最终解质量：以算法进程所得到的某些近似解为衡量标准，判断算法当前解的质量是否得到明显提高，从而确定是否终止算法。

（3）循环总数：即总的温度下降次数为一定值NK，当温度迭代次数达到NK时，停止运算。

4. 算例分析

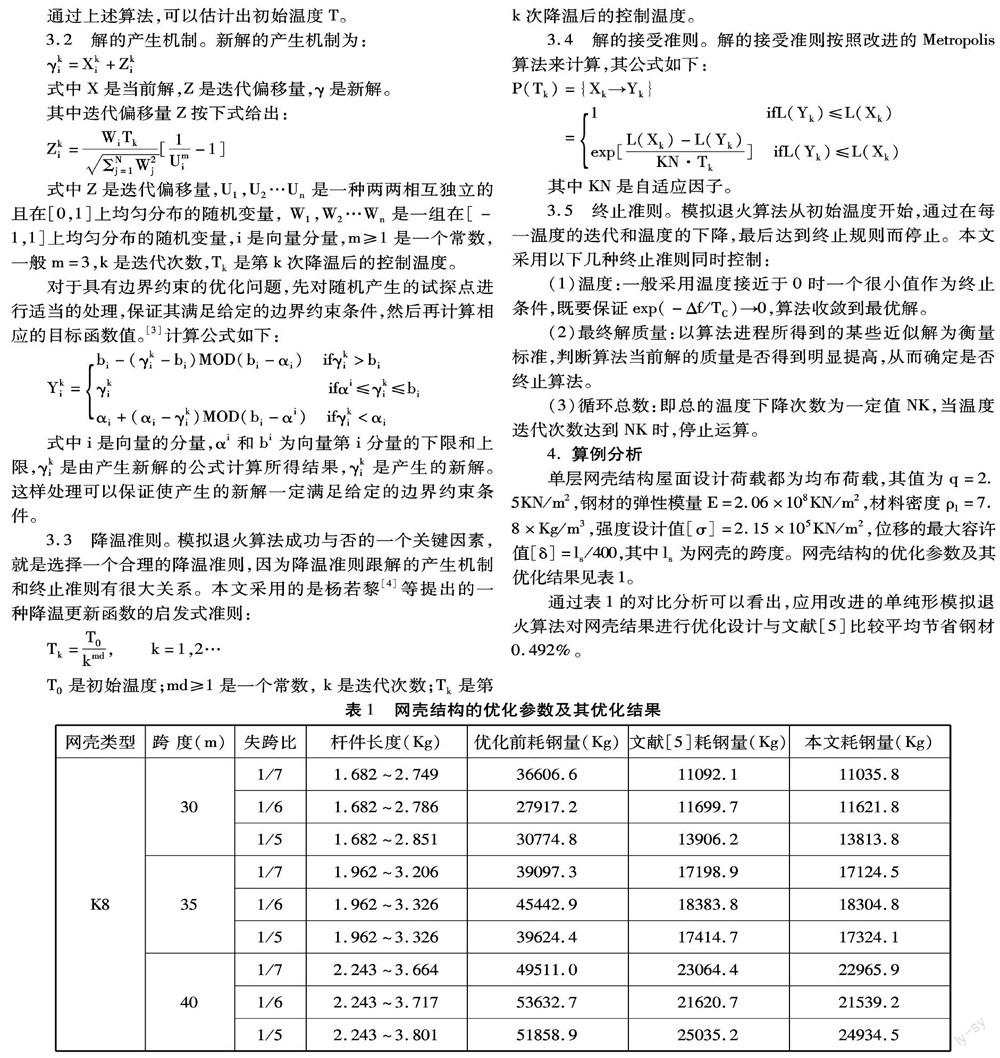
单层网壳结构屋面设计荷载都为均布荷载，其值为q=2.5KN/m²，钢材的弹性模量E=2.06×108KN/m²，材料密度ρl=7.8×Kg/m3，强度设计值[σ]=2.15×105KN/m²，位移的最大容许值[δ]=ls/400，其中ls为网壳的跨度。网壳结构的优化参数及其优化结果见表1。

通过表1的对比分析可以看出，应用改进的单纯形模拟退火算法对网壳结果进行优化设计与文献[5]比较平均节省钢材0.492%。

5. 结论

（1）SMSA算法将单纯形与模拟退火算法的优点有机的结合起来，既提高了局部搜索效率，又具有一定的全局收敛性。本文对算法中参数选择进行了探讨，算例表明本文对参数选取的改进是可行和有效的。使其应用于网壳结构优化设计成为可能。

（2）通过计算实例与文献的优化结果相对比，在满足强度、刚度、稳定性的条件下，SMSA算法在网壳结构优化设计中可以得到较好的优化结果。

参考文献

[1]王丰，王兴泰，于万瑞.改进模拟退火算法及其在电阻率图象重建中的应用[J].长春科技大学学报，1999，29（2）：175～178 .

[2]王凌.智能优化算法及其应用[M].北京：清华大学出版社，2001.

[3]项宝卫，胡永良，凌塑勇.桁架形状优化设计的模拟退火算法[J].力学与实践，2006，28（6）：46～50.

[4]杨若黎，顾基发.一种高效的模拟退火全局优化算法[J].系统工程理论与实践，1997，17（ 5）：29～35.

[5]刘宗发.单层球面网壳的选型优化设计[D].重庆：重庆大学，2005.