双曲率玻璃面优化拟合方法研究

刘晶 彭丹 杨平

【摘 要】文章在双曲率玻璃拟合方法的基础上进行了优化，并首次提出了双曲率玻璃面二次拟合算法，同时分析了拟合影响因子，给出了相对工程的标准方法。在该拟合方法的指导下，已经在UG NX平台上实现了自动优化程序的开发，经过了工程实践验证。

【关键词】汽车；玻璃面；双曲率；拟合；UG NX

【中图分类号】U463 【文献标识码】A 【文章编号】1674-0688（2016）01-0098-04

汽车车门双曲率玻璃面多以圆环面或者鼓形面进行拟合。即用规则几何体——圆环面或者鼓形面作为玻璃曲面的拟合目标，来使拟合的玻璃型面在长度和高度方向上都有弧度，使之符合车身外形走势。

本文在现有玻璃面运动和几何分析理论的基础上，提出双曲率玻璃面的二次拟合方法，进一步提高了拟合精度，并在UG NX平台上进行了验证。

1 技术背景

车门玻璃运动时上下转动运动和轴线方向移动的组合运动，考虑到车门导轨的生产方式，可以认为车门玻璃是在做螺旋运动。这种螺旋运动也就要求玻璃面边界近似拟合为螺旋线，同时要求运动过程中的边界误差小于一定的值，才能保证玻璃面运动光顺。

对于双曲率玻璃，近年国内研究也相对较多。大多以标准解析曲面为拟合目标，采用容差做法实现玻璃的双曲率设计。其中：圆环面拟合方法详细说明可以参照参考文献1。圆环面双曲率玻璃拟合设计思想如图1所示。

关于鼓形面拟合的详细说明可以参照参考文献2。鼓形面双曲率玻璃拟合设计思想如图2所示。

以上方法在工程中都存在诸多的限制条件，并非普适性的工具。

2 设计思想

采用圆环面拟合实现双曲率效果。设计思路中将面的形状和位置分开考虑，通过两次优化拟合操作分别确定。其中：一次优化目标获取和玻璃面最佳贴合的圆环面，确定大径、小径；二次优化调整圆环面的位置，使之和门框控制点的距离误差在许可范围内。

利用确定位置的圆环面，计算螺旋中心及半径，创建辅助圆柱。在辅助圆柱上计算螺旋线。最后投影回圆环面并偏置作为玻璃边界。

3 设计方法

3.1 一次优化

默认玻璃面UV中心作为起始变量点，将UV参数作为点的参数。分别过该变量点做玻璃面的UV曲线，将UV线拟合为圆弧（如图3所示）。

以大弧中心为原点，大弧方向为Z轴，小弧方向为X轴建立坐标系。由于曲面UV线不一定保持垂直关系，投影小弧到坐标系YZ平面上，再次将投影线拟合为圆弧（如图4所示）。

沿大弧中心回转二次拟合的小弧获得圆环面。

在玻璃面上选择4个点，测量它们到拟合面的距离，所得距离值的均方差作为优化目标。

优化程序通过修改变量点参数，反复比对优化目标，取最小值。此时看作拟合面和玻璃面是最佳贴合状态。

3.2 二次优化

圆环面的变化包括位置平移及角度变换，共6个参数控制。通过其中心坐标系的变换，来定位圆环面的变化位置。即将平移和角度变换6个参数作为优化输入参数。

作为设计要求，前后门各4个点，共8个点是需要进行控制的对象。在设计上，这8个点到圆环面的距离有特定的要求。设计可能会要求8个点到面距离相等，也可能要求上下距离不等，比如，需要考虑到干涉避让等。考虑到以上要求，将8个点到圆环面的距离测量值分别减去各自的要求距离，取平方和作为优化目标。这样当优化目标值最小时，可以看作是圆环面的最佳位置。

由于二次优化输入变量只有6个，因而无法保证需要优化的8个点全部同时到达完美要求。需要注意的是，优化是特定条件下的一种特定最优结果。

通过一次和二次优化，获得最能体现设计意图，并处于最佳设计位置的圆环面。

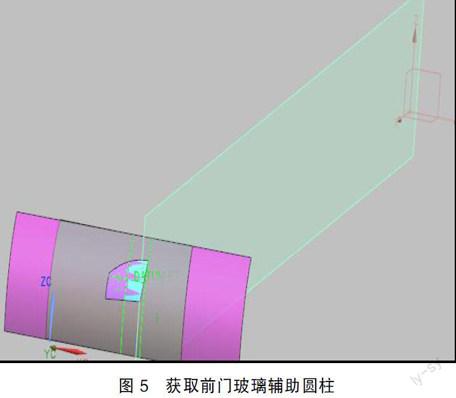
3.3 获取辅助圆柱

辅助圆柱是计算螺旋线的必要条件。考虑到靠近B柱區域玻璃边界较长，取用长边界拟合可以减少误差，在设计中在靠近B柱位置取圆环面的截面来拟合圆柱，前后玻璃面分别拟合。具体方法如下。

过圆环面中心轴和前玻璃后边界一点做辅助平面，辅助平面和圆环面的交线作为前玻璃辅助圆柱截面线。过圆环面中心轴和后玻璃前边界一点做辅助面，辅助平面和圆环面的交线作为后玻璃辅助圆柱截面线（如图5所示）。

3.4 计算螺旋线

原始玻璃面边界投影到辅助圆柱面，利用首尾点计算螺旋线。分别做首尾点到辅助圆柱中心的垂线，并测量升程和螺旋角，用于计算螺旋线。

螺旋参数化方程如下：

X（t）=r_front*cos（ang_front*t）

Y（t）=r_front*sin（ang_front*t）

Z（t）=-dist_front*t

其中，dist_front表示为螺旋角ang_front的升程。

后门螺旋线计算方法和前门计算方法相同，不再重复描述。

3.5 计算玻璃边界

玻璃面已经被拟合为圆环面，因而不可能生成标准的螺旋线，只能生成近似螺旋线（此处是容差做法，后续生产中对导轨要求较高，可能需要修改工艺，改为冲压法生产并进行整形操作）。

投影“步骤3.4”生成的螺旋线到优化后的圆环面上，并在面上偏置生成玻璃边界。

向前偏置获取前边界。投影上下边界到圆环面上，并偏置获取上下边界。

后车门玻璃做法相同，需要注意辅助圆柱有所不同。前后两辅助圆柱半径相同，而且都是从靠近B柱位置得到的截面线，轴线夹角不大，可以确保水切胶条断差在设计许可范围内。

3.6 裁剪边界

利用获取的边界修剪片体得到前车门玻璃。

4 运动检验

4.1 运动仿真

NX motion模块是NX用于机构运动和受力分析的模块，可以模拟各种刚体关节的运动。它对于汽车玻璃面的运动分析也适用。

本例中采用动力学分析环境，定义玻璃在导轨线上运动，分析其下落的不同位置情况。

经过在NX中进行验证，玻璃面可以表示出下滑打开的过程，并生成一系列中间过程状态，表达开窗过程中的各个位置。通过测量各个位置与初始面的面偏差和边偏差可以得知是否符合导轨设计要求。

由于玻璃是在导轨线上运动，加速度导致其运动速度是变化的，因此跟踪生成的各个位置体也不是等距的。

4.2 几何分析

通过对运动模型中连杆的自由度进行分析，可以总结出玻璃面的坐标规律，进而将运动学模型简化为数学模型进行分析和检测工作。运动学模型中通过三点定位，确定玻璃面的位置。如前门玻璃面，在数学模型中可以简化计算为后边界两端点A点、B点，前边界一点C点的位置确定方法。具体作图法如下。

（1）首先确定一点（如后边界上端点）在后边界导轨上，即A点。

（2）测量后边界点之间的长度，以上端点为球心做以测量长度为半径的球，交后边界于一点，即为B点。

（3）由于玻璃也是刚体，C点相对AB点的位置不变，因此可以预先求得C点到AB连线的投影点D。绕AB连线做半径为CD距离的环面，环面和另一导轨交点即为C点。

以上3个步骤确定了初始位置。

计算导轨在起始位置和窗台位置之间的行程，将行程曲线段按照等距原则等分为5份。这时可以得到5个点，分别针对这5个点执行上面3个步骤，就可以得到另外5个点的玻璃的等距运动位置。

相比之下，运动仿真开发一般会受到引力限制，不能实现等距。因此，推荐使用数学计算法处理。

4.3 软件实现

利用C++语言，进行NX二次开发实现了向导化处理。二次开发的程序采用向导化界面，将上述过程和逻辑固化下来。它简化了操作流程，并实现了标准化操作。

软件逻辑的实现，再次证明上述技术方案的逻辑可行性。玻璃面拟合工具如图6所示。

5 结语

本论文在上汽通用五菱汽车股份有限公司技术中心和天津达展科技有限公司技术部的大力支持下完成，并在UG NX平台上开发出了对应的自动化程序。经过实践检验，其设计效率和质量都有明显的提高。

本拟合方法跳出了制图法进行拟合的套路，提出了利用優化算法自动求取最佳拟合曲面的方法。同时进一步简化了运动学模型，提出了几何模型替代运动学模型的运动校核方法。最终通过UG NX软件实现了自动化流程操作，大大提高了汽车双曲率玻璃面拟合的精度和自动化程度。

作为应用型研究，玻璃面拟合方法研究也为汽车模块化设计提供了一些新的可借鉴思路。

参 考 文 献

[1]雷雨成，张平，陈寿昌，等.双曲率车门玻璃的圆环面拟合法[J].汽车工程，2005（5）.

[2]高大威，高云凯，周晓燕，等.基于鼓形面的车门玻璃及导轨设计[J].同济大学学报（自然科学版），2012（1）.

[3]姜连勃，王绍春.汽车车门设计[J].汽车技术，1999（4）.

[4]Ronald Goldman.计算机图形学与几何造型导论[M].北京：清华大学出版社，2011.

[5]陈文来.汽车造型设计中的玻璃面拟合研究[J].轻型汽车技术，2015（4）.

[6]郭长新.轿车侧窗玻璃导轨导引线工程优化设计[J].河南科技月刊，2012（8）.

[责任编辑：陈泽琦]