基于根轨迹法的飞机控制系统反馈设计

刘伯健

【摘 要】根轨迹法是经典控制理论中十分重要的一种直观的分析方法，由于它在设计反馈系统方面十分便捷、清晰，所以根轨迹法在飞行控制系统的设计上有着重要的应用地位。文章以根轨迹分析方法为基础，以F16飞机为模型，进行飞行控制系统的设计和分析，并用MATLAB仿真验证。

【关键词】根轨迹法；飞行控制；MATLAB

【中图分类号】V249 【文献标识码】A 【文章编号】1674-0688（2016）01-0040-03

随着现代控制理论的不断发展，经典控制理论不断受到冲击。但是经典控制理论中仍有很重要、很优良的分析方法值得学习研究。文章就以根轨迹法在飞行控制系统中的设计应用为例，说明经典控制理论在现代科学中仍有着十分重要的应用地位。

現代控制理论与经典控制理论是相辅相成的关系，并不是相互取代的关系，在控制系统的设计上，经典控制理论仍占有着不可替代的位置。经典控制理论是建立在频率响应法和根轨迹法的基础上，根轨迹法作为其中重要的一部分，是经典控制理论中对系统进行分析和综合的基本方法之一，并有着自己特殊的优势。根轨迹主要研究系统运动的稳定性、时间域和频率域中系统的运动特性、控制系统的设计原理和校正方法。

从1948年伊凡思（W.R.Evans）提出了根轨迹法后，通过运用根轨迹法就避免了求解特征方程困难的难题。它借助于参数连续变化，特征根在复平绘制出的轨迹来分析系统的特性，十分简便快速，并且在根轨迹图上可以轻松地找到参数的取值。但是绘制根轨迹曾经是个枯燥的工作，工作人员需要通过描点、计算、经验来绘制并不精确的根轨迹图，不过计算机技术发展以后，通过MATLAB成为一个十分简便绘制根轨迹的方法。

飞行控制系统是用来保证飞行器的稳定性和操纵性、提高完飞行品质、增强飞行的安全及减轻驾驶员负担的控制系统。它分为横向和纵向两个控制面。这两个控制面之间存在耦合和相互作用。本文设计仅针对于小扰动的忽略耦合作用的纵向面控制系统的反馈设计。设计要求减小荷兰滚模态对飞机的影响，并使系统能达到超调量小于5%，调解时间小于3 s的优良动态特性。由于飞机在不同的初始条件下配平参数不同、状态方程不同，所以文章仅就F16飞机在3 500 m，150 m/s的小扰动状态配平下进行设计（配平已给出）。下面我们就以根轨迹法为基础设计F16飞机的纵向控制反馈系统，并运用MATLAB进行仿真验证。

通过MATLAB中的Simulink功能构建飞机纵向系统的仿真模型，对于飞机纵向系统（即升降舵—俯仰角系统）来说，线性化过后的系统是一个单输入二输出的系统（q为机体轴俯仰角速率，alpha为迎角）。因此，我们构建如图1所示模型。

我们要想使升降舵—俯仰角系统有很好的动态特性，我们需要先提高升降舵—俯仰角速率系统的动态特性，使其达到一个优良的性能。因为升降舵—俯仰角速率系统的动态特性直接影响到升降舵—俯仰角系统的动态特性，若升降舵—俯仰角速率系统的动态特性不好，则可能会无法达到设计指标。因此升降舵—俯仰角速率系统的反馈设计十分重要。设计方法如下。

1 升降舵对应俯仰角速度测速反馈系统设计

运用Simulink中Gain环节构建反馈线路，如图2所示，从闭环系统结构图上不难看出，我们设计了一条反馈回路，它的实质是对于升降舵—俯仰角系统的一个测速反馈。我们需要设计反馈参数K的数值，使得方向舵—俯仰角速度系统有良好的动态特性即可。

我们根据开环根系统结构图中的A、B、C、D阵可以轻松得到开环系统的传递（以下传递函数均以此方法得到）：

G=■

由此函数，我们不难利用MATLAB的rlocus语句画出升降舵—俯仰角速度系统的根轨迹图（如图3所示，文中所有根轨迹图中K=Gain）。

根据根轨迹法分析，此系统是一个二阶系统，从根轨迹图上我们不难看出，K较小时，系统开始处于欠阻尼状态，随着增益的增加，阻尼比ζ增加，超调量会减小，ζ·ω增加，调节时间减小；当K等于0.188时，系统处于临界阻尼状态，对应的系统动态性能最好；K值再增大，调节时间就会过长。因此，我们不妨取K=0.188。至此升降舵—俯仰角速度系统设计完成，以此为基础，进行升降舵—俯仰角反馈系统设计。

2 升降舵对应俯仰角反馈系统设计

从simulink结构图4上我们不难看出，输出端口的qt是q1的积分，它表示的是俯仰角度。Gain4的值就是我们需要设计的升降舵—俯仰角系统的反馈参数值。

对于Gain4的设计，我们先得到此系统的开环传递函数：

G=■

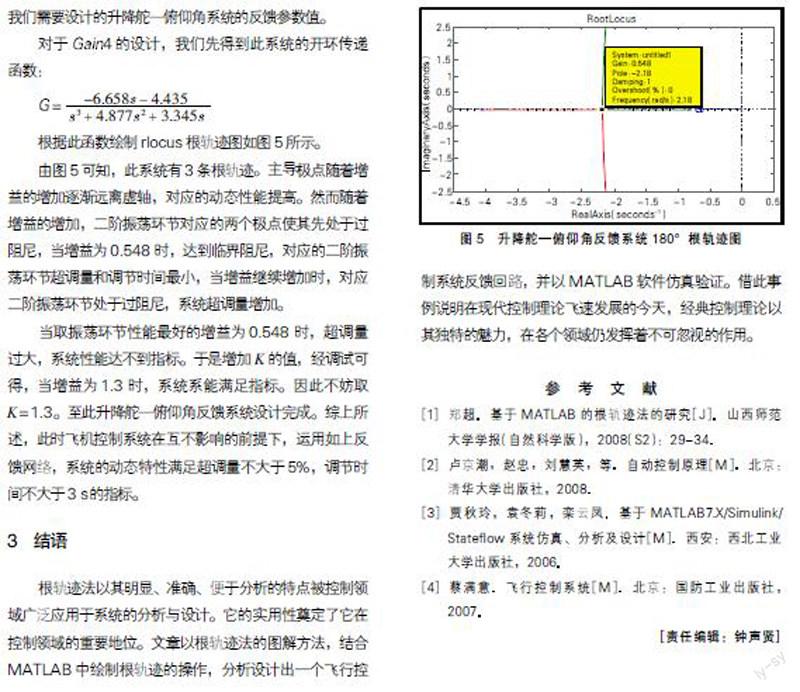
根据此函数绘制rlocus根轨迹图如图5所示。

由图5可知，此系统有3条根轨迹。主导极点随着增益的增加逐渐远离虚轴，对应的动态性能提高。然而随着增益的增加，二阶振荡环节对应的两个极点使其先处于过阻尼，当增益为0.548时，达到临界阻尼，对应的二阶振荡环节超调量和调节时间最小，当增益继续增加时，对应二阶振荡环节处于过阻尼，系统超调量增加。

当取振荡环节性能最好的增益为0.548时，超调量过大，系统性能达不到指标。于是增加K的值，经调试可得，当增益为1.3时，系统系能满足指标。因此不妨取K=1.3。至此升降舵—俯仰角反馈系统设计完成。综上所述，此时飞机控制系统在互不影响的前提下，运用如上反馈网络，系统的动态特性满足超调量不大于5%，调节时间不大于3 s的指标。

3 结语

根轨迹法以其明显、准确、便于分析的特点被控制领域广泛应用于系统的分析与设计。它的实用性奠定了它在控制领域的重要地位。文章以根轨迹法的图解方法，结合MATLAB中绘制根轨迹的操作，分析设计出一个飞行控制系统反馈回路，并以MATLAB软件仿真验证。借此事例说明在现代控制理论飞速发展的今天，经典控制理论以其独特的魅力，在各个领域仍发挥着不可忽视的作用。

参 考 文 献

[1]郑超.基于MATLAB的根轨迹法的研究[J].山西师范大学学报（自然科学版），2008（S2）：29-34.

[2]卢京潮，赵忠，刘慧英，等.自动控制原理[M].北京：清华大学出版社，2008.

[3]贾秋玲，袁冬莉，栾云凤.基于MATLAB7.X/Simulink/Stateflow系统仿真、分析及设计[M].西安：西北工业大学出版社，2006.

[4]蔡满意.飞行控制系统[M].北京：国防工业出版社，2007.

[责任编辑：钟声贤]