基于GARCH模型的恒生指数波动性预测评价

韩信 梁新潮 赖洪贵

【摘 要】以恒生指数1990年以来的数据为研究基础，为了研究基于GARCH模型的恒生指数波动率预测效果的评价，采用对原始数据进行了对数差分处理的方法，提取月对数收益率为研究样本，提出了一种通过计算误差率η值检验模拟步长和实际步长偏离程度的有效方法。建立在误差率计算的基础上，实验结果表明服从广义误差分布的GARCH模型建模拟合效果最好，但是对于基于GARCH模型的恒生指数波动率预测，服从正态分布的GARCH模型，预测一期效果最优，而对于多期的预测，服从偏t分布的GARCH模型最优。

【关键词】GARCH；波动率；恒生指数

一、引言

金融中的一个重要度量是资产相关的风险，而资产波动率也许是最常用的风险度量。波动率是日收益率的条件标准差，这是波动率的常见定义，本文所建立和讨论的正是这一类型的波动率模型。尽管波动率的定义很清晰，但是在实际中它并不能被直接的观测到，我们可以观测到的是资产和衍生品的价格。所以，我们需要从观测的价格来估计波动率，Engle（1982）提出了自回归条件异方差（Auroregressive Conditional Heteroscedatic， ARCH）模型，此模型能够很好的描述波动的持续性。基于ARCH模型，Bollerslev（1986）提出的广义自回归异方差模型（Generalized Autoregressive Conditional Heteroscedastic，GARCH）具有良好的处理厚尾的能力，而且GARCH能很好的处理有限数据量而造成的阶数过大问题，提高预测的精度。

香港作为世界的金融中心之一，股票市场开放程度非常高，对香港股票指数的研究，有利于揭示开放金融市场的股市发展阶段性特征。内地学界对于恒生指数的波动性也进行了一些研究，王娟（2012）通过设定残差分布的不同形式考察残差分布对建模的影响，再将GARCH 模型拟合出来的方差的值带入风险价值量模型中，从而得到精确度更高的VAR值。张咏梅（2015）所做的实证分析结果表明，恒生指数收益率序列具有明显的异方差性、波动性和持续性。但是国内对指数收益率预测方面的研究，多是基于上证或者深证指数的研究，郑振龙（2010）的研究发现时间序列模型适合于预测极短期的波动率，对中长期波动率的预测应采用隐含波动率方法。洪晶晶（2016）的研究发现以标准差定义的波动率建立GARCH（1，1）模型进行未来波动率预测的拟合效果较好。刘青（2015）采用一种半参数的方法评价模型预测的效果。

通过比较对前人研究成果的阅读发现，对于股票指数波动性预测效果的评价，并不尽人意，当前多采用方差估值的方法，比较复杂。本文试图通过对1990以来恒生指数的分析，建立多个GARCH模型，在比较不同模型优劣之后，以2015年12月为基点预测2016年1月到5月的恒生指数波动率，通过和实际波动率的比较，在对股票指数波动率预测评价上提出建立一种简易但十分有效的评价方法，即误差率评价的方法。

二、ARCH效应检验及GARCH模型

1.ARCH模型和ARCH效应检验

Engle（1982）提出的ARCH模型用于描述金融资产期望收益的时变性和金融资产方差的时变性，用于揭示了金融资产收益能力和风险特征。ARCH（q）模型可以表示为

2.ARCH效应

图2是过去25年间的月对数收益率时间序列图，从图中可以看出在一个大的波动后面往往出现一个较大的波动，而一个小的波动后面往往出现一个小的波动，表现出ARCH效应的特征，因而有必要进行ARCH效应检验，以证实月对数收益率是否存在ARCH效应。考虑月收益序列的相关性，有必要对月收益序列进行Box-Ljung检验，结果如表2说列示：月收益序列P值大于0.05说明月收益序列不存在自相关，也就是说月收益序列是一个白噪声序列。但是对于平方月收益序列的检验P值非常小，说明平方月收益序列存在自相关；ARCH检验的月收益序列p值为0.006228，远远小于0.05，表明月收益序列存在显著的ARCH效应，但平方月收益p值为0.2254，没有通过ARCH检验，表明平方月收益ARCH效应不显著。

图3（a）和图3（b）给出了月收益序列的样本ACF和PACF，表明在该对数收益率序列中没有强序列相关性，而图4（a）和图4（b）给出了平放月收益序列的样本ACF和PACF可以看出平方序列中有序列相关性，因而也就是进一步验证了恒生指数的月对数收益率有显著的ARCH效应。从以上分析可以得出，月收益序列存在显著的ARCH效应，因而可以针对月收益序列建立GARCH模型。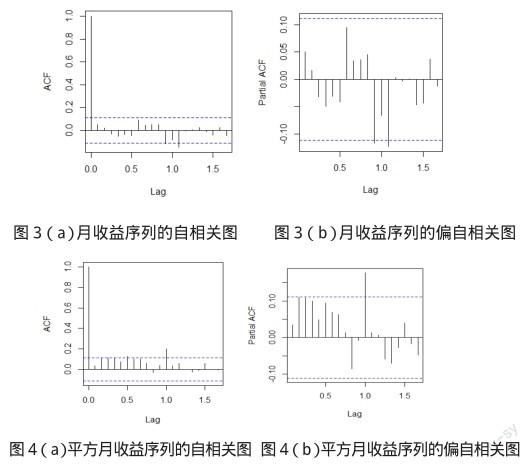

3.GARCH模型的选择

为了对未来收益率的预测，必须建立GARCH模型，这里构建服从标准正态分布的GARCH（1，1）和GARCH（1，2）模型，分别服从t分布和有偏t分布（ST）的GARCH（1，1）模型，分别服从广义误差分布（GED）和有偏的广义误差分布（SGEG）的GARCH（1，1）模型。

应用R语言中的fGarch软件包建立上述GARCH模型，得到的汇总数据如表2所示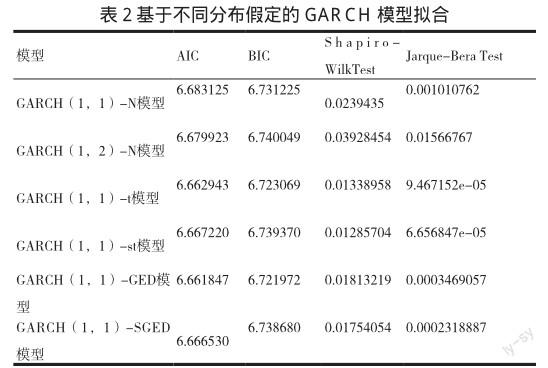

我们应用了6个GARCH模型对恒生指数月对数收益序列进行拟合，从S-W检验和J-B检验的结果看，所有的模型都通过了检验，说明模型的拟合程度都非常好，GARCH（1，1）-st模型的这两个检验的值最小，但依据AIC和BIC来选择模型的标准看GARCH（1，1）-st模型并不是最优的模型，GARCH（1，1）-GED模型最优。特别是从AIC值来看，虽然各个模型之间的差异非常小，但从存在的细微差异处，可以看出，基于广义误差分布和有偏广义误差分布的GARCH（1，1）模型拟合要分别优于基于t分布和广义t分布的GARCH（1，1）模型。

图5（a）和图5（b）分别表示GARCH（1，1）模型服从t分布和st分布的标准化残差图，从图形可以直观的表达模型的拟合情况还是非常理想的，不过图6（a）和图6（b）分别表示GARCH（1，1）模型服从GED和SGED分布的标准化残差图，显然图6的两图和图5相比，在拟合曲线的两侧落点更少，而且更加紧密，也进一步验证了服从GED和SGED分布要优于服从t和st分布的GARCH（1，1）模型。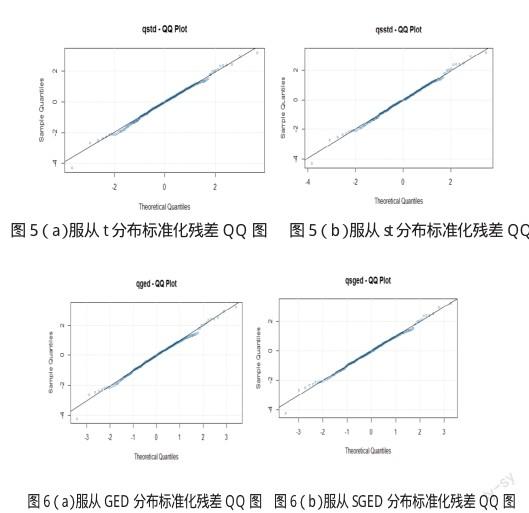

基于对所建立的模型的分析和选择，画出恒生指数从1990年1月1日到2015年12月31日的月对数收益率拟合的服从广义误差分布的GARCH（1，1）模型的时间序列图，如图7所示

四、预测与评价

1.GARCH模型预测

在GARCH模型预测中，最核心的是为条件方差（波动率）预测。由于波动率不能直接的观测得到，所以比较不同的波动率模型的预测表现是一个挑战。目前，比较通常的方法是利用样本外（outof-sample）预测法，这种预测方法是根据估计的模型对未来进行预测，该方法是对未来进行的估计，缺点是不能进行比较。本文也采用这种方法，设置2016年数据为样本外数据，以2015年12月为基点，对2016年恒生指数月对数收益的波动率进行预测，预测步长为5个月。

表3是假定服从不同分布的GARCH模型对恒生指数月对数收益波动率的预测，预测基点是2015年12月，期限为5个月，预测的步长如表所示，这一组数据的差别比较小，并不能足以说明预测模型的偏差程度。为了便于比较，表4给出了2016年以来5个月的恒生指数，依据不同分布的GARCH模型估计的实际步长。当然这里只有5期的数据，为了分析的一致性，对预测步长和实际步长的比较采用服从相同分布的GARCH模型。

2.评价

为了清晰的说明实际步长和预测步长的差异，这里引入一个自定义的公式，其值设为η

图8是基于不同模型计算的η值刻画的折现图。从这个图形可以直观的看出来，对于第一期的预测，各个模型拟合的都非常好，其中GARCH（1，1）-N模型的拟合最好，误差率只有0.7%。但是随着步长测增加，服从标准正态分布的GARCH模型的误差率要高于其他模型，特别是服从正态分布的GARCH（1，2）模型的预测效果最不理想。从整体而言，从第二期以后的误差率呈下降趋势，这或许可以说明，随着步长的增加，预测效果会更好些。就各个模型而言，有偏的t分布和有偏的广义误差分布预测效果要分别好于标准的t分布和标准的广义误差分布。更进一步说，模拟效果最好的两个分布是有偏的t分布和标准的t分布，这一发现或许有利于改进波动率预测的方法。

五、 结论

本文基于GARCH模型，探讨了香港股市的波动性，实证结果表明：香港股票市场具有很强的波动聚集性和持续性，收益率曲线具有明显的尖峰厚尾性，可以进行波动率预测的研究从建模的结果看，高阶的GARCH模型拟合效果低于低阶的模型的拟合效果，基于广义误差分布和有偏广义误差分布的GARCH（1，1）模型拟合要分别优于基于t分布和广义t分布的GARCH（1，1）模型。本文提出了一个直观上比较预测模型优劣的方法，即计算误差率η值，从验证效果，这个方法比较借鉴，易于比较从预测的结果看，对于GARCH模型的波动率预测，第一期最好选用服从正态分布的GARCH模型，而如果预测的期数较多则最好选用服从有偏的t分布的GARCH模型。建模拟合程度高的模型，预测模型的结果未必是最好的，这一点对于选择预测模型的时候，存在参考意义。对于多期的步长预测，理论上讲，预测的步长越长，误差率存在缩小的趋势。

参考文献：

[1]. Engle， R.F.， AUTOREGRESSIVE CONDITIONAL HETEROSCEDASTICITY WITH ESTIMATES OF THE VARIANCE OF UNITED KINGDOM INFLATION. Econometrica， 1982. 50（4）： p. 987-1007.

[2]. Bollerslev， T.， GENERALIZED AUTOREGRESSIVE CONDITIONAL HETEROSKEDASTICITY. Journal of Econometrics， 1986. 31（3）： p. 307-327.

[3]. 张咏梅， 一种基于Eviews的Garch模型的恒生指数研究. 统计与决策， 2015. No.422（02）： p. 159-161.

[4]. 郑振龙 and 黄薏舟， 波动率预测：GARCH模型与隐含波动率. 数量经济技术经济研究， 2010. v.27（01）： p. 140-150.

[5]. 洪晶晶 and 吴鹏跃， 基于GARCH模型的金融市场波动性分析与预测. 价值工程， 2016. v.35；No.405（01）： p. 46-47.

[6]. 刘青， 戴经跃， and 杨超， 基于GARCH族模型的收益波动率预测绩效评估方法. 统计与决策， 2015. No.429（09）： p. 160-163.

作者简介：

韩信（1990—），男，安徽宿州，集美大学财经学院，2015级，税务硕士，研究方向：金融税制。

梁新潮（1960—），男，江西余干人，集美大学财经学院教授，硕士研究生导师，研究方向：财政金融理论与政策 。

赖洪贵（1990—），男，福建龙岩人，中南财经政法大学金融学院，2014级房地产经济学硕士研究生，研究方向：房地产金融与投资。