蚁群算法在搜索引擎系统中的应用研究与改进

赛忠良

【摘要】：齐心协力搬运食物，这是我们心里最深刻的蚂蚁行为，人类对蚂蚁行为的研究发现，蚂蚁可以在没有任何帮助的情况下找到窝巢到食物的最短路径，并且当环境变化时，依旧可以顺应环境变化找到新的路径，有人就以蚂蚁的这种“群集智能”提出了蚁群算法。

众所周知，搜索引擎的主要工作过程包括：抓取、存储、页面分析、索引、检索等几个主要过程。随着互联网的迅猛发展，对搜索引擎的性能要求越来越高，搜索引擎系统的体系结构和搜索算法从根本上决定了整个系统的效率和搜索性能，由此可知，搜索算法在搜索引擎重要性举足轻重，本文章首先介绍了蚁群算法的工作原理，以及蚁群算法在搜索引擎方面的应用现状和以及提出的的改进问题。

【关键词】：算法;搜索引擎;蚁群算法

引言

蚁群算法最早由意大利学者Marco Dorigo（及其导师Colorni）于1911年在其博士论文

中提出，后期工作则是Marco Dorigo与其合作同事们在比利时布鲁塞尔自由大学研究期间陆续展开，早期的研究成果大多是该研究团队在欧洲的一些小型专业研讨会及其会议录上所发表的，世界对此了解并不多，1998年十月，首届蚂蚁优化国际研讨会于比利时布鲁塞尔自由大学召开，此后，几乎每年都召开一次这样的会议并出版回忆录，吸引了来自世界各个国家的同行，还为蚁群算法开设了专题小组讨论和研习班，蚁群算法自提出以来，以TSP为测试基准，与其他一些常用启发式方法作了一系列的比较，对若干典型的对称性于非对称性TSP问题（如TSPLIB中的许多实例），先后采用了模拟退火法，遗传算法，神经网络（如弹性网法，自组织映射法等）。进化规划，遗传退火法，插入法，禁忌搜索法，边交换法等多种优化算法进行求解，除了Lin-Kernighan局部改进法之外，蚁群算法优于其他的所有方法蚁群算法的基本原理，毫无疑问，蚁群算法表现出了强大的优势性。

本文就蚁群算法的原理以及搜索引擎方面研究作出綜述，并就做出的的改进进行研究。

1蚁群算法的原理

蚂蚁是如何找到窝巢与食物源的最短路径的？蚂蚁通过在移动中所释放的特有分泌物-信息素来找寻窝巢与食物源的最短路径。

1.1蚂蚁的觅食原理

自然界中的蚂蚁没有视觉，既不知道向何处去寻找和获取食物，也不知道发现食物后如何返回自己的巢穴，它们仅仅依赖于同类散发在周围环境中的特殊物质-信息素的轨迹，从而决定自己何去何从，有趣的是，尽管没有任何经验的只是，但蚂蚁们还是有能力找到从其巢穴到十五元的最佳路径，是指在该路线上放置障碍物之后，它们仍能很快重新找到续保的最佳路线。

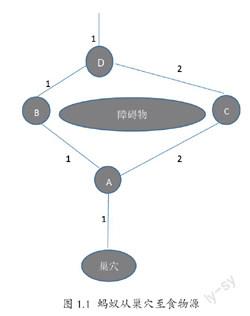
在这里，我借助更形象化的图示来理解这种机制，假定障碍物的周围有两条道路可以从蚂蚁的巢穴到食物源（见图1.1）：Nest-ABD-Food和Nest-ACD-Food，分别具有长度4和6，蚂蚁在单位时间内看可以移动一个单位长度的距离，开始时所有道路上都未曾留有任何信息素。在t=0时刻，20只蚂蚁从巢穴出发移动到A，它们以相同概率选择左侧或右侧道路，因此平均有10只蚂蚁走左侧，10只蚂蚁走右侧，在t=4时刻，第一组到达食物源的蚂蚁将折回，在t=5时刻，两组蚂蚁将在D点相遇，此时BD上的信息素数量与CD上的相同，因为各有10只蚂蚁选择了相应的道路，从而有5只返回的蚂蚁将选择BD，而另5只将选择CD。在t=8时刻，前5个蚂蚁将返回巢穴，而AC，CD和BD上各有5个蚂蚁。在t=9时刻，前5个蚂蚁又回到A并且再次面对往左还是往右的选择，这时，AB上的轨迹数为20而AC上的为15，因此将有较多的蚂蚁选择往左，从而增强了该路线上的信息素，随着该过程的继续，两条道路上的信息素量的差距越来越大，直至绝大多数蚂蚁都选择了最短的路线。

正是由于一条道路要比另外一条短，因此在相同时间区间内，短的路线会有更多的机会被选择，例如，在96个时间单元中，短的路线将会被一个蚂蚁走过12次，而长的路线仅仅被走过8次。

图1.1  蚂蚁从巢穴至食物源

1.2蚁群算法的基本原理

这里，以TSP问题为例，阐述蚁群算法的基本思想和原理：

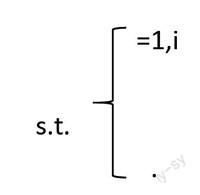
在基本的实施步骤中，用到的变量和常数有：

m=蚂蚁的个数，

=边弧（i，j）的能见度（visibility），即1/，

=边弧（i，j）的轨迹强度（intensity），

按的不同取法，可形成不同类型的蚁群算法，最基本的为

=蚂蚁K的转移速率，与成正比，j是尚未访问的节点，轨迹强度的更新方程为=+〖.这里，个参数的含义如下：

轨迹的相对重要性（）;

= 能见度的相对重要性（）;

轨迹的持久性（01）;可將1—理解为迹衰减度

Q= 体现蚂蚁所留轨迹数量的一个常数.

步骤1. nc0（nc为迭代步数或搜索次数）;各和初始化;将m个蚂蚁置于n各顶点上;

步骤2. 将各蚂蚁的初始出发点置于当前解集中;对每个蚂蚁k，按概率移动至下一个顶点j，将顶点j置于当前解集;

步骤3. 计算各蚂蚁的目标函数值;记录当前的最好解;

步骤4. 按更新方程修改轨迹长度

步骤5. 对各边弧（i，j），置;ncnc+1;

步骤6. 若nc<预定迭代次数且无退化行为，则转步骤2.

步骤7. 输出最好解.

整个算法的时间复杂度为O（nc），如果选取m≈n，则蚁群算法的时间复杂度为O（nc）.算法理论认为，这个复杂度在计算时间上是可以接受的.

2蚁群算法与搜索引擎的研究

2.1搜索引擎的结构

搜索引擎结构由两部分组成：离线（Ofltine）部分和在线部分（Online）离线部分通过网页爬取器（Crawler）、网页剖析器（Parser）和索引编辑器（Index Builder）组成，主要完成对网页的收集、剖析、索引和重要排序功能在线部分通过用户界N（UserInterface）、缓存（Caching）和相关性排序为用户返回搜索结果。

2.2蚁群算法在搜索引擎中的应用研究

蚂蚁是根据自己活动时释放的信息素以及对信息素浓度的判断来找到最短路径的，搜索引擎系统是将访问网站的用户看成是蚂蚁来指引用户进行导航，建立蚁群的导航模型是基于用户在网页之间随机的进行转移，随后，实时的抽取用户的导航行为为特征，从而抽取用户的访问网页的具体信息。

用户导航路径：

当用户访问具体的网站时，相关的网络请求称为用户的导航路径，换句话说就是用户的浏览行为。

支持度：根據用户的导航路径，可以建议一个有向图，支持度表示用户沿着节点i到j路径的访问频率，定义如下：

=/

表示沿着节点i到j路径访问的次数，从节点i到所有的下一节点有n种不同的选择。

信息素函数：

信息素函数（t）表示用户沿着节点i到j路径的访问倾向，定义如下：

）+，表示信息素的衰减率.

公式中表示沿节点i到j路径访问下一个网页的平均时间，从节点i到所有的相邻节点有n种不同的选择。

公式中表示沿着节点i到j路径访问下一个网页的时间，表示沿着节点i到j路径的访问次数。

用户导航路径的核心特征就是用户在不同网页间的访问时间，在网页上的访问时间可以很好地度量用户对该网页的兴趣，如果对网页内容感兴趣，他可能在浏览该网页上花费更多的时间，如果用户仅仅是通过网页的一个链接到达另一个网页，他可能在该网页上逗留很短的时间。

偏好函数：偏好函数（t）表示用户沿着节点i到j路径访问的偏好，偏好函数定义如下：

公式中分别表示信息素和支持度的相对重要性。

3蚁群算法的应用改进

3.1扩展旅行商问题的蚁群算法

3.1.2 问题阐述

瓶颈问题问题是最早从TSP延伸出来的样子红扩展性TSP，其含义与经典的TSP类似，仅仅是目标不同，要求巡回路线中经过的最长距离最短，即最小化瓶颈距离，该情况体现了那些不追求总巡回路线最短，而只希望在巡回路线中每次从一个地点至另外一个地点的单行程尽可能短的实际应用问题的特征。

从严格的数学意义上来讲，瓶颈TSP可以通过一定的方法转化为等价的经典TSP问题，由于增加了问题的规模，因此并没有降低问题的难度，也未能提供任何特殊的解题方法。

和经典TSP类似，瓶颈TSP的数学模型可写成

min Z=max

由于目標函数值为瓶颈值，故求得的巡回路线与经典TSP的巡回路线往往截然不同。

3.1.3 算法思想

求解瓶颈问题的蚁群算法思想和经典TSP类似，只需要将目标函数值转换为瓶颈值即可，对瓶颈TSP求解采用：（1）最远插入法;（2）最近插入法;（3）最小插入法;（4）最近邻法;（5）模拟退火法;（6）蚁群算法;（7）元胞蚁群算法。

4结束语

本文讨论了蚁群算法的基本原理，以及蚁群算法在搜索引擎系统中的相关应用，并对蚁群算法的一些改进应用进行了研究探讨。

参考文献：

[1] 王艳玲，李龙澍，胡哲.  群体智能优化算法[J]. 计算机技术与发展. 2008（08）

[2] 王剑，李平，杨春节.  蚁群算法的理论与应用[J]. 机电工程. 2003（05）

[3] 刘道海，方毅，黄樟灿.  一种求解组合优化问题的演化算法[J]. 武汉大学学报（理学版）.2002（03）

[4] 李冰岩，黄地龙，郝园.  基于Web的搜索引擎算法的研究[J]. 电脑与电信. 2010（05）

[5] 王海鹰，魏颖.  基于蚁群算法的多目标网页综合评价策略[J]. 计算机工程与应用. 2011（04）

[6] 邢立宁，陈英武，姚锋，贺仁杰，姜江.求解双层CARP优化问题的知识型蚁群算法[J]. 系统工程理论与实践. 2012（11）

[7] 马良，朱刚，宁爱兵，蚁群优化算法[J]. 科学出版社.2008（05）