北斗中长基线静态解算算法实现及结果分析

应俊俊　张京奎

摘 要：该文对北斗中长基线静态基线解算的算法模型进行了介绍，基于北斗双频观测数据，对站间小高差和站间大高差中长基线的解算精度进行了测试和分析。实测结果表明：站间小高差基线各时段解算精度均优于平面1 cm+1 ppm，高程2 cm+2 ppm；站间大高差基线绝大部分时段解算精度均优于平面1 cm+1 ppm，高程2 cm+2 ppm，在解算时段长度为4 h时，解算精度优于平面1 cm+1 ppm，高程2 cm+2 ppm的时段比例高于95%。

关键词：北斗 中长基线 静态基线解算 站间高差 时段长度

中图分类号：P228.4 文献标识码：A 文章编号：1672-3791（2016）06（b）-0143-03

静态基线解算在大地控制网布设和控制点加密中具有重要应用，主流GNSS数据处理软件有Trimble的TBC、Leica的LGO、Novatel的WayPoint、中海达的HGO等。虽然北斗静态基线解算原理与GPS类似，但由于北斗星座设计的特点，站星几何图形变化较慢，载波相位观测量间具有很强的相关性，造成方程严重病态，北斗系统在基线解算的理论研究和应用方面正在展开，相关的实验分析还需要进行大量的工作。

对于中长基线而言，电离层、对流层等误差的空间相关性减弱，导致双差残余的电离层、对流层等误差较大，以致影响浮点模糊度的精度，增大模糊度固定难度。为了得到正确的模糊度整数值，中长基线情况下需要考虑电离层延迟误差和对流层延迟误差的影响。通常，电离层延迟采用双频消电离层组合进行消除，对流层延迟通过干延迟改正和湿延迟参数估计的综合处理进行消除。其中，对流层延迟与站间高差关系密切，一般而言，站间高差越大，对流层延迟的影响越显著。

该文着重对北斗中长基线静态解算中的算法模型进行阐述，对站间大高差和小高差解算结果进行分析，文中所有数据均采用自研的北斗静态基线解算软件进行数据处理。

1 中长基线静态解算的算法实现

静态基线解算通过对载波进行双差组合（首先在站r和站b间进行单差，再基于卫星间进行双差），此时接收机钟差已消除，则其双差观测方程为：

（1）

（2）

其中：和分别为双差载波（测相伪距，单位为m）和码组合观测量；为伪距观测量的双差值；为相应频点的波长；为双差模糊度；为电离层延迟误差；为对流层延迟误差；和分别为载波和码残余误差（观测噪声和未模型化误差）。

在进行解算时，对流层延迟通过干延迟GPT/GMF改正和湿延迟参数估计进行消除，电离层延迟采用双频消电离层组合进行消除。中长基线静态解算主要基于上述公式，具体做法为：基于长时间观测数据，首先使用宽巷载波双差数据列立观测方程，求解出宽巷模糊度；其次将宽巷模糊度代入消电离层组合观测方程中，估计模糊度浮点解和坐标（隐含在中）；再次通过搜索方法对模糊度浮点解进行取整；最后将模糊度整数解代入到上述方程中，得到精确的基线坐标。

2 基线精度测试

为了获得较全面的基线精度统计结果，分别选取不同长度、不同站间高差基线进行测试，数据情况及测试结果如下所述。

2.1 站间小高差基线测试结果

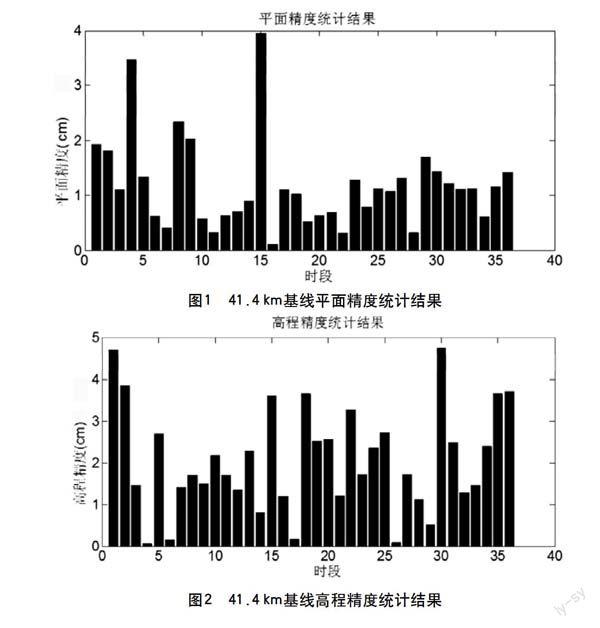
中长基线站间小高差测试以2014年1月华北地区某次测试为例，基线长为41.4 km，站间高差为37 m，A、B、C这3种型号在B1、B2双频接收机均进行了48 h测试，解算模式为双频消电离层模式，高度角为15°，4 h为一个时段，模糊度搜索方法为Lambda方法，Ratio阈值为2.5，对流层处理方式为对流层干延迟改正、湿延迟估计。以LGO软件长时间观测、分时段解算的GPS基线结果为真值，平面精度统计结果如图1所示，高程精度统计结果如图2所示。其中，1～12时段为A型接收机测试结果，13～24时段为B型接收机测试结果，25～36时段为C型接收机测试结果。

从图1、图2可看出，解算的各时段平面精度均优于1 cm+1 ppm，高程精度优于2 cm+2 ppm；平面精度总体优于高程精度；3种型号接收机解算结果存在一定的差异，尤其表现在平面精度。此种现象的存在，可能与接收机内部噪声水平和稳定性相关。

2.2 站间大高差基线测试结果

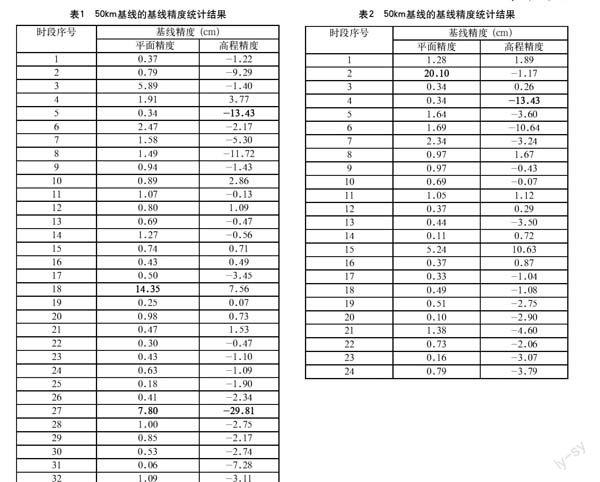
为对大高差数据进行测试，从香港CORS站下载HKWS、HKNP两站2015年8月26日、2015年11月25日、2016年2月24日、2016年6月1日共4天96 h测试数据分别进行解算。HKWS、HKNP两站基线长为49.89 km，站间高差为286.88 m。解算频点为北斗B1、B2双频、电离层为双频消电离层模式，高度角为15°，采样间隔为30 s，模糊度搜索方法为Lambda方法，Ratio阈值为2.5，分别以2 h、3 h、4 h为一个时段进行处理。以香港地政总署网站给出的2016年4月1日CORS站坐标为真值进行精度评估，时段长度为3 h的基线精度统计结果如表1所示，时段长度为4 h的基线精度统计结果如表2所示，表3为不同时段长度基线精度超限百分比统计结果。

为便于对精度结果进行对比统计，平面精度以1 cm+1 ppm、高程精度以2 cm+2 ppm为限值，对于HKWS、HKNP两站近50 km基线，平面精度限值为6 cm，高程精度限值为12 cm。表1、表2中以黑色加粗字体标识的即为平面精度超过6 cm、高程精度超过12 cm的精度数据。表3为以此限值为基准的平面精度和高程精度超限百分比统计结果。

从表1、表2可看出，除少数超限时段外，其他解算时段的平面精度均优于1 cm+1 ppm，高程精度优于2 cm+2 ppm；平面精度总体优于高程精度。从表3可看出，随时间增加，平面精度和高程精度超限百分比逐渐下降，在时段长度为4 h时，平面精度和高程精度达标百分比均高于95%。

3 结语

该文对北斗中长基线静态解算的算法模型进行了介绍，对不同长度、不同站间高差的基线进行了测试和分析。结果表明：站间小高差基线各时段解算精度均优于平面1 cm+1 ppm，高程2 cm+2 ppm。站间大高差基线在时段长度为4 h时，平面精度优于1 cm+1 ppm，高程精度优于2 cm+2 ppm的比例高于95%。

参考文献

[1] 王胜利，王庆，聂文锋，等.北斗系统高轨卫星高精度定位模型病态性分析及改进方法[J].导航定位学报，2013，1（3）：31-32.

[2] 邱晓璐，刘根友，段鹏硕，等.GPS/BD载波相位定位病态性对比分析[J].测绘科学，2015，40（7）：24-28.

[3] 元荣.BDS/GPS基线算法研究及软件开发[D].北京：清华大学，2014.

[4] 张明，刘晖，范城城.基于对流层加权法的网络RTK快速初始化研究[J].测绘地理信息，2015，40（6）：19-21.