Bayes评分与BIC评分对简单Bayes网络结构学习结果复杂度的影响

刘晓亮

摘要：在基于评分-搜索的Bayes网络结构学习算法中，评分函数的选取对学习的结果具有关键影响。文章利用随机给定的观测数据，采用Bayes评分函数和BIC评分函数，对一些节点数较少的Bayes網络进行穷举式结构学习，并对学习结果的复杂度进行了测算和分析。仿真实验表明，在相同的观测样本下，采用BIC评分函数将得到比采用Bayes评分函数更简单的Bayes网络。

关键词：Bayes网络；网络结构；学习结果；复杂度；Bayes评分；BIC评分 文献标识码：A

中图分类号：TP181 文章编号：1009-2374（2016）18-0188-02 DOI：10.13535/j.cnki.11-4406/n.2016.18.094

Bayes网络可以用有向图的形式形象地表示出考虑的对象间的概率依存关系。与传统数据挖掘方法相比，它具有理论基础牢固、推理简单准确，且可以在丢失数据的不完备信息下进行推理等诸多优势，因此，基于Bayes网络的数据挖掘算法在通信编码、图像处理、生物医学工程等方面都具有相当广泛的应用。

由于Bayes网络的广泛应用，自然希望能够根据现有的先验知识和观测数据自动训练出对象间的Bayes网络，这就是Bayes网络的学习问题。这一问题可分为两类：参数学习和结构学习。所谓参数学习，就是在已知Bayes网络的结构（即所考虑对象间的条件独立性质）后，利用观测数据估计出个节点处的相应参数（即为已知该节点父亲节点时该节点的概率分布函数）；结构学习指的是在考虑变量的相互关系未知的情况下，利用观测数据对它们之间的关系进行估计，从而训练出相应的Bayes网络结构。显然，结构学习是比参数学习更困难、更有挑战性的任务。

目前有关结构学习的算法研究主要分为两类：一类是基于条件独立性检测的算法。这类算法主要通过检查变量间鉴别信息或交叉熵等方法来判断变量间的条件独立性，再建立满足这些条件独立性的Bayes网络。该方法的计算量较小，在节点数不多的情况下准确度也较高，但在节点数较多的情况下，对条件独立性的不准确判断造成的误差会产生连锁反应，导致学习结果的准确性大大降低。第二类算法是基于评分-搜索的结构学习算法。这类算法首先确定一个能够反映Bayes网络准确度的评分函数，然后在满足节点数要求的全体Bayes网络中采用启发式搜索等办法，找出使得评分函数尽量大（或小）的网络作为学习结果。由于这一问题是NP问题，在节点数较大的情况下无法求出最优解，所以搜索算法一般为梯度下降、蒙特卡洛等次优算法。基于评分-搜索的结构学习算法因其出色的准确性和对观测数据的鲁棒性而成为结构识别算法中的主流。在基于评分-搜索的结构学习算法中，评分函数的选取对于学习结果的性能是具有关键性影响的。好的评分函数可以在模型的准确性与复杂性之间做出合适的权衡，对之后将学习结果用于推理时的效率会有很大提高，目前被广泛采用的评分标准有Bayes评分、BIC评分等。本文的目的即为研究这两种评分对于学习结果复杂性的影响。本文以下的部分将这样安排：第1部分介绍Bayes评分和BIC评分的原理；第2部分介绍仿真实验的设计；第3部分对实验结果进行初步分析；第4部分给出结论。

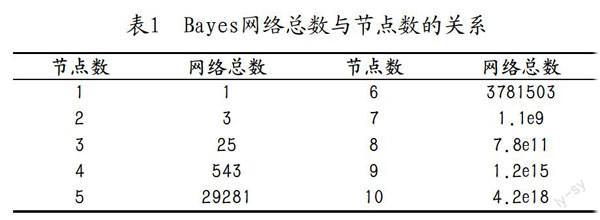
为了研究评分函数对于学习结果的影响，必须排除搜索算法可能造成的干扰。由于随着节点数的增加，全部可能的Bayes网络总数将以超指数的速度增长（见表1），因此对于节点数较多的情况，穷举搜索是不可能的。考虑到为了精确得到学习结果平均复杂度而需要进行的试验次数，本文中只对节点数为2、3、4的情况进行研究。

1 Bayes评分和BIC评分的原理

在基于评分-搜索的结构学习算法中，评分函数是用来衡量各Bayes网络对数据匹配程度的指标，其自变量为某Bayes网络结构，函数值越大（小），则该Bayes结构对数据匹配得越好。在定义评分函数时，往往考虑两个因素：模型匹配数据的精确程度和模型的复杂度。学习算法总是倾向于简单却精确匹配数据的Bayes网络结构。

目前广泛使用的评分函数主要有Bayes评分和BIC评分，下面分别介绍其原理：

1.1 Bayes评分

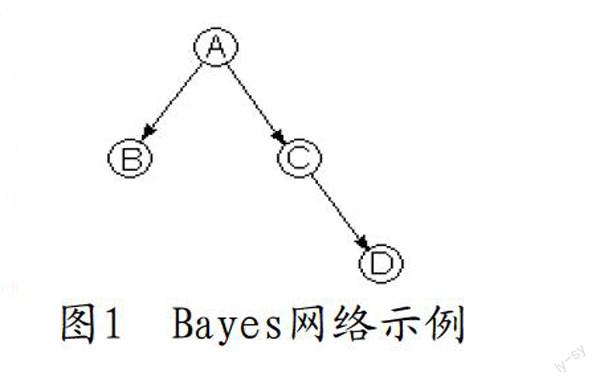
为了完全确定一个Bayes网络，仅仅知道其结构是不够的，还应当知道决定该结构下各变量条件概率的参数。图1所示的4节点Bayes网络，假设各节点均为布尔变量，则需要确定的自由参数共有

p（A=0），p（B=0|A=0），p（B=0|A=1），p（C=0|A=0），

p（C=0|A=1），p（D=0|C=0），p（D=0|C=1）共

7个。

在Bayes评分函数的定义过程中，假设所有的自由参数组成的参数向量为Θ，并记观测到的数据序列为X，则结构S的Bayes评分定义为在Θ满足在参数空间中均匀分布的条件下观测到X的后验概率的对数值。即：

假设所有观测值相互独立，且所有变量均为布尔取值，则由积分公式可以推出：

式中：n为节点总数为节点的父亲节点集合；为满足节点的父亲节点处于状态j（共种状态）且的观测样本总数；为满足节点的父亲节点处于状态j且的观测样本总数，。

1.2 BIC评分

Bayes评分假设结构确定时自由参数在参数空间中满足均匀分布，这一条件实际上隐含了对结构复杂度的限制。因为复杂的结构其参数空间维数一般较大，因此使得观测数据的后验概率较大的参数在整个参数空间中所占比重自然较小，这样平均后的结果会降低该结构的Bayes评分值。另一种常用的评分函数——BIC评分则把对结构精确性和复杂性评估分为两项。假设各参数定义与上节相同，则结构S的BIC评分定义为：

式中：d为自由参数个数（图1中d=7）；N为观测变量总数。上式中第一项为针对模型精确性的评估，而第二项是针对模型复杂度的惩罚。

假设所有观测值相互独立，且所有变量均为布尔取值，则结构的BIC评分函数可以简化成：

2 实验设计

下面通过MATLAB仿真实验研究两种评分方法对于学习结果复杂度的影响。仿真实验涉及的Bayes网络节点数仅限于2、3、4，观测样本数目限于5～50。

对所有节点数i，观测样本总数j，则每个观测样本可能出现的所有状态数为。随机生成观测数据矩阵A。该矩阵为N行列，其中N为试验次数，实际设N=1000，每行为一次试验的数据样本，该行每个元素分别代表本次实验中状态j的出现次数[如A（k，1）为第k次实验中所有变量均为0的次数，A（k，）为第k次实验中所有变量均为1的次数]。有。

用MATLAB编写结构识别程序，其中为了避免搜索算法的影响，采用穷举法搜索，并采用相应评分最高的Bayes网络作为学习结果，用该网络自由参数个数作为其复杂度。对每组（i，j）所得到的1000个复杂度取平均作为节点数为i，观测样本数为j时的平均学习复杂度和。对每个i做出两种评估函数关于j的曲线并加以比较，从而得到评分函数和学习结果平均复杂度的关系。

3 实验结果和初步分析

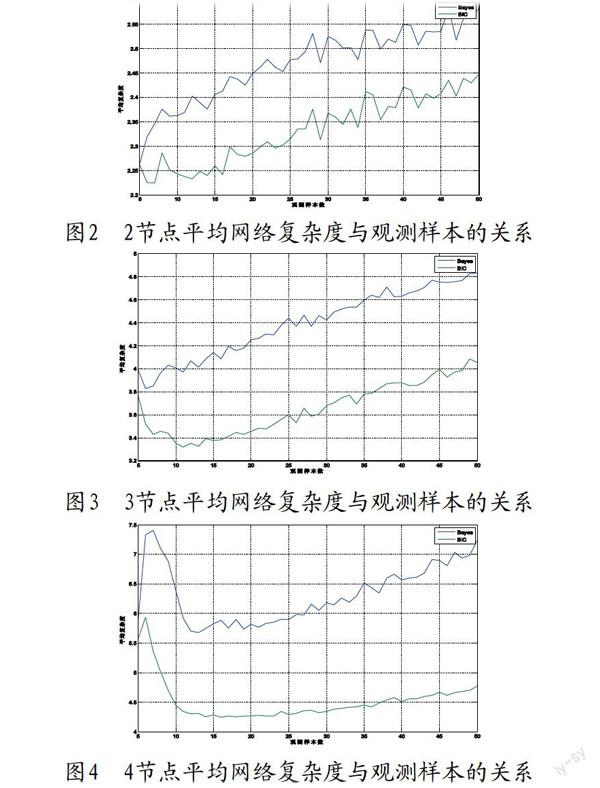
节点数i=2、3、4时的仿真结果分别如图2、图3、图4所示：

由图2、图3、图4可以得到以下结论：（1）在样本数较多的情况下，随着样本数的增多，学习结果的复杂度也会提高；（2）在同样的观测条件下，BIC评分的学习结果比Bayes评分的学习结果更为简单，且随着节点数的增加，这种复杂度上的差异会越来越大；（3）随着样本数的增加，BIC评分训练结果复杂度的增加幅度要慢于Bayes评分。

综上所述，可以发现，BIC评分相比于Bayes评分而言，更倾向于选用简单的网络。

4 结语

本文对基于评分-搜索的Bayes网络结构学习算法的两种主流评分函数——Bayes评分和BIC评分对于学习结果复杂度的影响进行了分析。仿真结果表明，BIC评分在精确性和简单性的权衡中更倾向于接受简单的Bayes网络。这一结论说明：在运算资源有限且对训练精度要求不高的应用环境中，BIC评分是比Bayes评分更优秀的评分原则。

参考文献

[1] N.Friedman.Learning belief networks in the presence of missing values and hidden variables[J].machine learning international workshop then conference，1997.

[2] N.Friedman.The Bayesian EM structural Algorithm[J].Proc.UAI，1998.

[3] JM Pena，JA Lozano，P Larranaga.An improved Bayesian structural EM algorithm for learning Bayesian networks for clustering[J].Pattern Recognition Letters，2000.

[4] D Heckerman.A tutorial on learning with Bayesian networks[J].Learning in Graphical Models，1998.

[5] GF Cooper E Herskovits.A Bayesian method for the induction of probabilistic networks from data[J].Machine Learning，1992.

（責任编辑：周 琼）