铅球的最佳抛射角和最小出手速度

易子喻

摘 要：随着教育改革的不断深入，素质教育背景下，物理教材中添加了很多生活化、探究性的内容，这些内容对培养学生的思维能力，灵活运用所学知识的能力有着显著的作用。因此，该文结合高中物理必修2中的探究性内容“铅球的最佳抛射角和最少出手速度”进行分析，并结合相关例题，总结出一些更好理解斜抛运动知识点和解题的方法，以供参考。

关键词：物理 抛射角 出手速度

中图分类号：G633.7 文献标识码：A 文章编号：1672-3791（2016）07（c）-0110-02

体育课是学生十分喜爱的一门课程，体育课中的各种竞技活动，都渗透着物理学知識，二者关系紧密。同时随着教育改革的深入，纵观历年高考题目会发现，高考命题逐渐贴近生活，增加了更多贴近生活的探究性题目，这就要求学生能够从生活中提取物理现象、规律，同时要学会利用所学的知识解决生活中的实际问题。

1 问题的提出

高中物理必修2中，关于斜抛运动的典型题目就是铅球的最佳抛射角和最少出手速度。根据教材上的内容，学生潜意识会存在这样一个认识——抛射铅球的最佳角度为45°角，也就是只要以45°角抛射铅球，就能获得最大的射程。事实上这种认识是错误的。

《物理》（必修2）教材就对此提出了疑问：铅球的最佳抛射角是45°吗？教材给出的命题中提出，在水平面上，以初速度（v）斜抛某物体，若忽略空气阻力，那么该物体回落到同一平面时，射程以抛射角45°时最大。但事实上，抛射铅球时，铅球的抛射点与落至地面的点存在高差h，若以同样的初速度抛射铅球，改变抛射角（如45°和40°），当铅球落至抛射点同一水平面时，45°角射程最大；而铅球落到地面时却是40°的抛射角获得的射程较大。

教材上对此并未做出详细解释，同时若学生查阅相关资料会发现，专业的铅球运动员在确定最佳抛射角时更加复杂，这会给学生学习斜抛运动的知识点带来一定的困扰。因此，学生在学习中必须要深入理解其中的规律，方能确保后续的灵活应用[1]。

2 铅球的最佳抛射角和最少出手速度

根据上文提出的问题，假设抛射铅球的初速度为v，抛射角为α，时间为t，铅球重量为g，建立坐标系。（如图1）

如图1所示，在初速度一定的情况下，由于抛射点与地面存在高差，在确定抛射角α时，应分别考虑两种情况。

2.1 回落至抛射点所在平面时

对于公式（7），可利用导数或不等式的知识进行求解，比较直观，但数学推导过程难度大，学生掌握起来比较困难。除此外，以学生的知识体系来看，可以利用矢量的知识求解。如果能够转变思维角度，通过速度矢量三角形以及合理变形，则可快速求解[2]。

因此，假设铅球速度：，那么，可以据此建立矢量三角形。（如图2）

根据能量守恒：，可得：当初速度v不变时，也会不变。

根据公式（1）可知，如果要获得最大的值，那么只需使获得最大值。分析该公式，可以发现等式右边的就是图2所示三角形的面积，而在图示三角形中为定值，要获得最大的面积，显然就需要，那么可得公式：。也就是说当时，可获得最大的射程，即：。

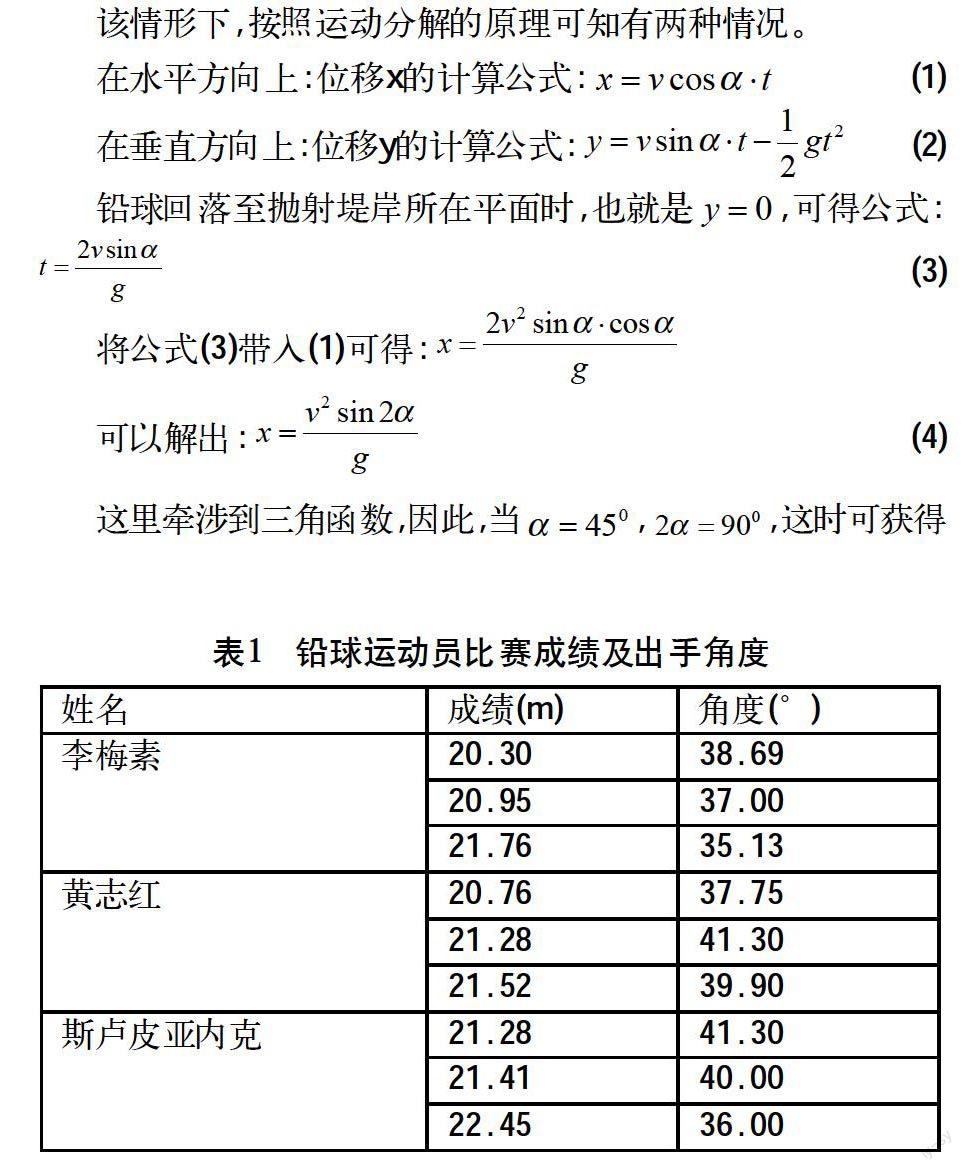
由此可以推断，铅球的最佳抛射角度和抛射点高度、初速度有关。当初速度不变，抛射点与落点存在高差时，最佳抛射角并不固定。而就铅球运动员来说，其身高、出手速度也存在差异，因此，抛射铅球的最佳角度也存在差异。如表1所示。

学生在学习中，通过上述的方法进行分析，能够有效掌握斜抛运动的规律及其应用，并且也会对矢量的知识点产生更深入的认识。学生研究其中的规律时，能够获得思维能力的提高，同时，也能加强物理与数学等其他学科的联系。有兴趣的学生，可以利用数学中的导数和不等式的知识点尝试推导上文的公式（7），加深对斜抛运动知识点的理解，同时还可以获得综合应用所学知识的能力，拓展思维，提高解题能力[3]。因此，下文以实际例题进行分析。

3 结语

学生在学习斜抛运动的知识点时，要带着科学的研究态度深入了解斜抛运动知识点当中蕴含的物理现象和规律，综合考虑其中的影响因素，方能准确理解其中的内涵。而在理解这一部分知识时，又会涉及到其他的相关知识点，这也是对学生所学知识的一个巩固过程。以目前的高考命题趋势看，题目开始贴近生活实际，探究铅球的最佳抛射角和最少出手速度这样贴近生活实际的题目，是巩固学生所学知识，并灵活应用的典范，作用十分显著。

参考文献

[1] 尤明庆.关于铅球最佳出手角的讨论[J].力学与实践，2013（1）：67-68.

[2] 龚劲涛，吴英.两种求铅球最佳出手角的方法比较[J].物理与工程，2011（3）：6-8，11.

[3] 龚劲涛，任全红，冯文林.巧解铅球最佳出手角[J].力学与实践，2011（5）：60，61-62.