一种新的基础矩阵估计算法研究

魏晓艳

摘 要：该文提出了一种新的估计基础矩阵的鲁棒算法——基于粒子群算法的最小平方中值法（PSO-LMedS）。该方法是将最小平方中值法（LMedS）与粒子群算法（PSO）相结合，将LMedS方法得到的匹配点对作为PSO的初始种群，利用粒子群算法的全局优化特性，通过不断的寻优过程，估计得到最佳基础矩阵，提高基础矩阵估计精度。通过仿真实例，证明改进后的算法具有较高的鲁棒性和精确性。

关键词：极线几何 基础矩阵 粒子群算法 最小平方中值法

中图分类号：TP301.6 文献标识码：A 文章编号：1672-3791（2016）01（c）-0148-03

Abstract：This paper proposes a new robust algorithm（PSO-LMedS） for estimating fundamental matrix.This new algorithm views matching points obtained by LMedS as the initial population in PSO，then improves fundamental matrix estimation accuracy by using global optimization characteristics of PSO.Finally，it uses the new approachestimate the fundamental matrix，and the simulation results show high robustness and accuracy.

Key Words：Epipolar geometry；Fundamental matrix；PSO；LMedS

对于两幅待匹配的图像，极线几何关系是可以获得的唯一一组信息，该关系是对未定标图像进行分析的一种基本工具。极线几何关系可以通过一个3×3的矩阵来表示，即基础矩阵（F阵）。对基础矩阵的估计是三维重建问题、运动估计问题、像机标定问题、匹配和跟踪等问题研究的基础，因此，对其估计问题的研究已经成为人们研究的一个重要方向。该文主要针对基础矩阵的估计问题进行研究[1-2]。

1 常用的基础矩阵估计方法

常用的基础矩阵估计方法有线性方法、迭代方法以及鲁棒方法。在估计基础矩阵的各种算法中，线性算法是最基本的，其实现简单，计算速度快，其缺点是对误匹配和噪声比较敏感；迭代算法和鲁棒算法需要线性算法为其提供好的初值，不论是迭代算法还是鲁棒算法都是反复调用线性方法[3]。

常用的鲁棒估计算法有M-估计法、最小平方中值法（LMedS）及随机采样一致方法（RANSAC）[4]。该文基于鲁棒方法的思想在LMedS的基础上进行了改进，提出了一种基于粒子群算法的最小平方中值法——PSO-LMedS，来提高基础矩阵的估计精度。

2 一种改进的基础矩阵估计算法研究

2.1 PSO算法

随机初始一群粒子，每个粒子既不包括体积信息，也不包括质量信息，可以将每个粒子都看作为优化过程中的一个可行解，对于粒子的好坏，可以通过一个事先设定好的适应度函数来进行确定。优化过程中，每个粒子都将在可行解空间中进行运动，由一个速度变量决定其方向和距离。通常情况下粒子将追随当前的最优粒子，并经过不断的迭代搜索最后得到全局最优解。在每一次迭代过程中，粒子都将会跟踪两个最优值：一个是粒子本身迄今为止找到的最优解，即局部最优解；另一个是整个粒子群体到目前为止找到的最优解，即全局最优解。

其中n为所有的匹配对数目，p为子集的大小。当（其中推荐值为2.5）时，则认为该匹配对是正确的；否则就是错误的匹配对。

（5）将上述由最小平方中值法得到的匹配点对作为粒子群算法的初始种群，同时初始化相关参数：搜索空间的上限和下限，学习因子，收敛精度，粒子位置及速度范围。

（6）评价每一个粒子：按照公式（2）计算粒子的适应值，如果优于当前最优解，则将其设置为该粒子的位置且更新最优解，更新粒子序号。

（7）按照式（1）更新每个粒子的位置及速度，并做越限处理。

（8）按照公式（2）重新计算各粒子的适应值，将每个粒子的当前位置的适应值和当前最好位置的适应值相比较，如果当前位置适应值优于最优解的适应值，则进行更新。

（9）是否满足终止条件，该文中选取最大迭代次数，如果达到最大迭代次数时，则转到步骤（10），否则转入步骤（7），迭代次数增加一次。

（10）输出结果，即最佳基础矩阵F。

3 仿真实验

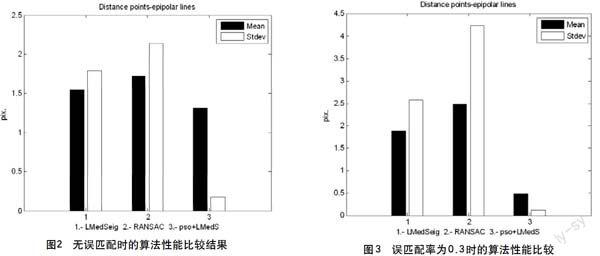
为了验证基于粒子群算法的最小平方中值法估计基础矩阵的有效性及优越性，下列将八点算法（LMedSeig）、随机采样一致方法（RANSAC）及该文所提出的改进的基础矩阵估计算法（PSO-LMedS）进行性能的比较。用两匹配点偏离对应极线的距离（对极距离）的平均值及方差来评价其性能。首先选取图1中的图像进行图像特征点的检测与匹配，得到初始的匹配点对。分别采用8点算法、RANSAC算法以及PSO-LMedS，利用图1 c图中得到的初始匹配点对，进行基础矩阵的估计。采用公式（2）来计算所有有效匹配点对的对极距离d，采用对极距离的均值（Mean）及方差值（Stdev）来表征估计得到的基础矩阵的精确性。

图2中描述了没有加入误匹配点时3种不同算法的性能比较结果，其中黑色直方图表示对极距离的平均值，白色直方图表示对极距离的方差；可以看出，PSO-LMedS的均值和方差较小，较其他几种方法的精度都高；然而在实际计算过程中，PSO-LMedS计算时间较长，这是因为在计算的过程中，不仅先要对outliers进行剔除，同时对利用不同的匹配点对求的基础矩阵进行了寻优过程，以便找到最佳基础矩阵，因此较为耗时。

图3为加入30%的误匹配点时的性能比较结果，由仿真结果可以看出，PSO-LMedS在计算精度方面较其它几种算法都具有一定的优势。

4 结语

该文将PSO与LMedS相结合，提出了一种新的基础矩阵估计方法——PSO-LMedS。仿真结果表明：改进后的算法提高了基础矩阵的估计精度，验证了算法的有效性。

参考文献

[1] 陈泽志，吴成柯，刘勇.对极几何估计的鲁棒性新算法[J].西安电子科技大学软件学报，2000，23（6）：634-639.

[2] 胡凌山，朱齐丹.计算机视觉中基本矩阵的估计方法[J].应用科技，2005（10）：41-43.

[3] 陈杰，刘松林，宇超群.一种改进的基本矩阵鲁棒估计算法[C]//《测绘通报》测绘科学前沿技术论坛摘要集.2008.

[4] 钟慧湘.基本矩阵计算方法的研究[D].吉林大学，2005.

[5] 宋汉辰，张小义，吴玲达.一种基础矩阵线性估计的鲁棒方法[J].国防科技大学学报，2005，31（15）：178-179，185.