人体肩部形态对肩点获取的影响研究
洪正琳 乐逸朦 吴尚 尚笑梅


摘 要:肩点作为三维的测量基准点,其判断的准确性受多方面影响。本文主要研究人体不同的肩部形态对肩点获取的影响。肩点获取是否准确可以从以肩点为基准点的人体测量部位的尺寸波动情况来判断,此次人体测量实验共采集了230名被测者的人体数据。对左肩高、右肩高、肩宽直、肩宽弧、臂根围、全臂长6个部位尺寸进行分析,发现肩斜度对肩点获取的影响不显著,而冲肩对肩点获取的影响显著,导致测量数据较为不准确。
关键词:人体测量;肩部形态;肩斜;冲肩;肩点
中图分类号:TS942.17 文献标志码:B 文章编号:1674-2346(2016)03-
人体各部位尺寸信息是量体裁衣的基础,国家服装号型标准都是以大量人体测量数据为基准而得出覆盖率较广的服装号型尺寸。影响服装用人体数据测量时数据准确性的主要因素为测量者的技能水平、测量环境、基准点的定义难度、基准点的运动范围、测量路径等,其中基准点的定义难度、基准点的运动范围会影响基准点获取的准确性,从而导致测量结果不稳定。[1-2]肩点在服用人体测量时和很多数据相关,如左肩高、右肩高、肩宽直、肩宽弧、臂根围和全臂长,因此肩点的准确获取是这些数据测量准确性的保证。服装样版绘制时这些数据会影响小肩宽、落肩量、袖长、袖窿弧长等的确定。影响基准点获取准确性的共性因素有基准点的定义难度、基准点的运动范围等,肩点获取的个性因素中人体肩部形态不容忽视。
《服装用人体测量的部位与方法》规定肩点是肩胛骨的肩峰外侧缘上向外最突出的点。[3]判断肩点时被测者保持站姿,手臂自然下垂,测量者站于被测者正面,用目光确定肩斜线和与手臂三角肌切线,这两条线相交的角平分线与肩部的交点即为肩点。肩点获取时需依据肩斜线,溜肩、平肩、高低肩肩斜不同,冲肩体肩斜线不易获取,因此本文从人体肩部形态着手去研究肩点获取情况。[4]
1 肩部形态分析
人体肩部作为服装的支撑部位,其形态对于服装的造型表现至关重要,因此西装会加垫肩来衬托阳刚之气。肩部形态分为肩斜度的不同和肩端点前冲量的不同。根据肩斜可将肩部形态分为溜肩、平肩、高低肩和正常肩,根据前冲量不同可将肩部分为前冲肩和正常肩。[5]测量颈肩点的
水平线与肩线的夹角,正常肩夹角为19°到22°,小于19°者为平肩,大于22°者为溜肩。[6-7]前冲肩体型就是肩端点前冲量较大,会使服装穿着的原有造型受到破坏。肩斜度和前冲肩程度都会对肩点的获取产生影响,在进行手工人体测量时,测量者是通过目测肩斜线与手臂切线的交线的平分线来寻找肩点的,因此不同肩斜度情况下肩斜线的判断难易会不同。前冲肩体型对于从被测者背后获取肩点和正面获取肩点会产生较大差异。
依据肩点获取的定义,我们绘制出不同肩斜角度下的肩点位置变化情况。由图1所示,保持手臂斜度不变,在肩斜度越来越大的情况下,肩点的位置会向下偏移。肩点是肩斜线与手臂切线夹角的角平分线与肩部的交点,在肩斜度增大的情况下,肩斜线与手臂切线交点也会向下偏移,造成了肩点的向下偏移。[8]
2 人体测量实验
2.1 实验目的 图1 肩斜示意图
采集大量人体数据,对不同于常体的肩斜程度和不同冲肩程度的被测者进行记录,将被记录的被测者测体数据与肩部常体测体数据进行对比分析,找出人体肩斜程度以及冲肩情况与肩点获取之间的关系。
2.2 实验设计
本次人体测量实验的测量者、记录者、被测者均为女性。参与此次实验的测量者共9名,测量者均熟练掌握人体测量技能,人体测量经验丰富;记录者共9名,记录者均熟悉测量流程,数据记录经验丰富,记录认真细致;被测者为18~23周岁在校女大学生。测量地点为学校人体测量教室,温度、湿度均适宜。测量工具有软尺、三角板、直尺。为消除测量者过于注意肩点的紧张感,此次人体测量实验采取常规测量,即采用测量者熟悉的测量流程和部位,共测量27个部位尺寸和1个体重数据。[9]每位被测者接受任意3位不同测量者的测量,且3位测量者对被测者需进行不连续的3次测量,记录者会确保每一位被测者进行符合要求的9次测量。由于此次实验数据将用来做肩部形态对肩点获取情况的分析,记录者会对平肩、溜肩、高低肩和冲肩体型的被测者进行备注,各体型备注各不重复,只备注特征最明显的一种。
2.3 实验结果
此次人体测量实验共采集了230名被测者的人体数据,对异常值数据进行剔除后得到224名被测者的有效数据,其中有27名被测者被记录为溜肩体型,16名被测者被记录为平肩体型,34名被测者被记录为高低肩体型,14名被测者被记录为冲肩体型。实验共得到人体测量数据2016组,计算每一位测量者3次测量的平均值,可以得到672组数据。筛选出其中和肩点有关的测量部位(左肩高、右肩高、肩宽直、肩宽弧、臂根围、全臂长)的数据,部分数据如表1所示。
表1 部分测量部位的部分测体数据
被测者 测量次数 左肩高/cm 右肩高/cm 肩宽直/cm 肩宽弧/cm 臂根围/cm 全臂长/cm
004 1 123.8 122.5 37.7 42.5 33.0 51.2
2 123.5 123.0 38.0 43.0 34.2 50.7
3 123.5 122.5 37.8 42.6 32.1 51.3
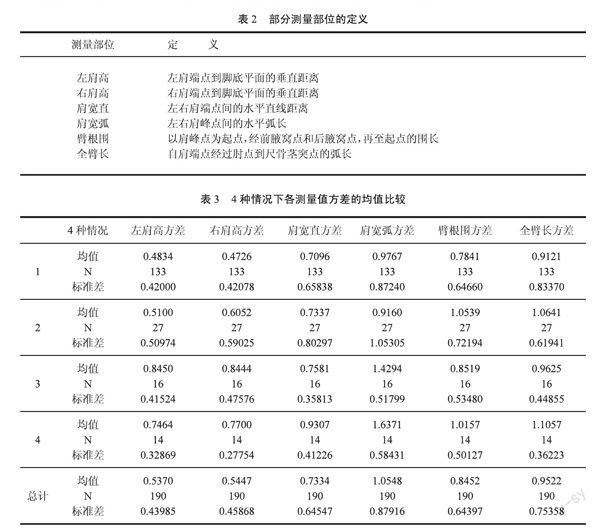
表1中测量次数是指被3位测量者测量,表中数据均是每一位测量者测量某一被测者3次数据的平均值。此次用作数据分析的6个测量部位的定义如表2所示。
表2 部分测量部位的定义
测量部位 定 义
左肩高 左肩端点到脚底平面的垂直距离
右肩高 右肩端点到脚底平面的垂直距离
肩宽直 左右肩端点间的水平直线距离
肩宽弧 左右肩峰点间的水平弧长
臂根围 以肩峰点为起点,经前腋窝点和后腋窝点,再至起点的围长
全臂长 自肩端点经过肘点到尺骨茎突点的弧长
2.4 实验数据分析
首先对实验结果进行处理,计算每位被测者左肩高、右肩高、肩宽直、肩宽弧、臂根围、全臂长测量值的方差。不同被测者同一部位的测量值存在很大差异,因此无法直接通过测量值去判断测量的准确性。方差是反映数据波动情况的数学量,方差大,表明被测者被不同测量者测量的数据差异大,差异的大小表明了测量的准确性。在此次实验中,左肩高、右肩高、肩宽直、肩宽弧、臂根围、全臂长这6个部位的测量准确性和肩点获取情况有关[10]。
4种情况 左肩高方差 右肩高方差 肩宽直方差 肩宽弧方差 臂根围方差 全臂长方差
1 均值 0.4834 0.4726 0.7096 0.9767 0.7841 0.9121
N 133 133 133 133 133 133
标准差 0.42000 0.42078 0.65838 0.87240 0.64660 0.83370
2 均值 0.5100 0.6052 0.7337 0.9160 1.0539 1.0641
N 27 27 27 27 27 27
标准差 0.50974 0.59025 0.80297 1.05305 0.72194 0.61941
3 均值 0.8450 0.8444 0.7581 1.4294 0.8519 0.9625
N 16 16 16 16 16 16
标准差 0.41524 0.47576 0.35813 0.51799 0.53480 0.44855
4 均值 0.7464 0.7700 0.9307 1.6371 1.0157 1.1057
N 14 14 14 14 14 14
标准差 0.32869 0.27754 0.41226 0.58431 0.50127 0.36223
总计 均值 0.5370 0.5447 0.7334 1.0548 0.8452 0.9522
N 190 190 190 190 190 190
标准差 0.43985 0.45868 0.64547 0.87916 0.64397 0.75358
表3 4种情况下各测量值方差的均值比较
将肩部常体记为情况1,溜肩体型记为情况2,平肩体型记为情况3,冲肩体型记为情况4。高低肩体型是两肩高度不一致,因此左右肩会呈现出不同的肩斜度,这和溜肩、平肩相对应,因此不对高低肩体型做进一步分析。先对4种情况下各测量值方差的均值进行比较,得到表3。肩部正常体型的测量数据的波动性是此次实验数据分析的标准,再将其他3种情况下与肩点相关的6个部位测量值的方差分别与情况1中测量值的方差进行两个样本的独立T检验,得到表4、表5、表6。
表3显示了不同情况下测量值方差的基本统计量,均值显示了样本的平均大小,标准差显示了样本的离散情况。通过表3可以看出,情况3中数据的离散程度最大,有的测量值方差的均值在4种情况下很接近,如肩宽直和全臂长;有的测量值方差的均值在4种情况下存在很大差异,如肩宽弧;其他测量值如左肩高、右肩高、臂根围方差的均值也存在一定的差异。
表4 溜肩体型与肩部常体测量值方差两个样本的独立T检验
方差方程的 Levene检验 均值方程的 t 检验
F Sig. T df Sig.(双侧) 均值差值 标准误差值 差分的95%置信区间
下限 上限
左肩高方差 假设方差相等 1.816 0.180 -0.289 158 0.773 -0.02662 0.09204 -0.20841 0.15517
假设方差不相等 -0.254 33.535 0.801 -0.02662 0.10464 -0.23938 0.18615
右肩高方差 假设方差相等 2.883 0.091 -1.386 158 0.168 -0.13255 0.09563 -0.32143 0.05633
假设方差不相等 -1.111 31.575 0.275 -0.13255 0.11931 -0.37571 0.11060
肩宽直方差 假设方差相等 2.140 0.145 -0.167 158 0.868 -0.02408 0.14444 -0.30936 0.26120
假设方差不相等 -0.146 33.458 0.885 -0.02408 0.16474 -0.35907 0.31091
肩宽弧方差 假设方差相等 0.090 0.764 0.318 158 0.751 0.06071 0.19095 -0.31643 0.43785
假设方差不相等 0.281 33.621 0.781 0.06071 0.21632 -0.37909 0.50050
臂根围方差 假设方差相等 1.442 0.232 -1.938 158 0.054 -0.26984 0.13923 -0.54483 0.00515
假设方差不相等 -1.801 34.975 0.080 -0.26984 0.14982 -0.57401 0.03432
全臂长方差 假设方差相等 1.031 0.312 -0.897 158 0.371 -0.15197 0.16937 -0.48649 0.18255
假设方差不相等 -1.090 47.378 0.281 -0.15197 0.13941 -0.43237 0.12843
表5 平肩体型与肩部常体测量值方差两个样本的独立T检验
方差方程的 Levene检验 均值方程的 t 检验
F Sig. T df Sig.(双侧) 均值差值 标准误差值 差分的95%置信区间
下限 上限
左肩高方差 假设方差相等 0.086 0.770 -3.258 147 0.001 -0.36162 0.11101 -0.58100 -0.14224
假设方差不相等 -3.287 18.887 0.004 -0.36162 0.11001 -0.59197 -0.13126
右肩高方差 假设方差相等 1.123 0.291 -3.292 147 0.001 -0.37174 0.11291 -0.59489 -0.14860
假设方差不相等 -2.988 17.938 0.008 -0.37174 0.12441 -0.63318 -0.11030
肩宽直方差 假设方差相等 3.875 0.051 -0.289 147 0.773 -0.04850 0.16784 -0.38019 0.28319
假设方差不相等 -0.457 29.130 0.651 -0.04850 0.10618 -0.26563 0.16863
肩宽弧方差 假设方差相等 1.314 0.254 -2.029 147 0.044 -0.45270 0.22309 -0.89358 -0.01182
假设方差不相等 -3.019 26.631 0.006 -0.45270 0.14997 -0.76062 -0.14478
臂根围方差 假设方差相等 0.134 0.714 -0.403 147 0.688 -0.06781 0.16832 -0.40044 0.26483
假设方差不相等 -0.468 20.667 0.645 -0.06781 0.14498 -0.36961 0.23399
全臂长方差 假设方差相等 4.664 0.032 -0.237 147 0.813 -0.05039 0.21246 -0.47026 0.36947
假设方差不相等 -0.378 29.480 0.708 -0.05039 0.13342 -0.32307 0.22228
表6 冲肩体型与肩部常体测量值方差两个样本的独立T检验
方差方程的 Levene检验 均值方程的 t 检验
F Sig. T df Sig.(双侧) 均值差值 标准误差值 差分的95%置信区间
下限 上限
左肩高方差 假设方差相等 2.171 0.143 -2.269 145 0.025 -0.26305 0.11594 -0.49220 -0.03389
假设方差不相等 -2.766 17.801 0.013 -0.26305 0.09510 -0.46300 -0.06309
右肩高方差 假设方差相等 3.485 0.064 -2.581 145 0.011 -0.29737 0.11520 -0.52505 -0.06969
假设方差不相等 -3.597 19.937 0.002 -0.29737 0.08266 -0.46984 -0.12490
肩宽直方差 假设方差相等 2.487 0.117 -1.229 145 0.221 -0.22109 0.17988 -0.57661 0.13443
假设方差不相等 -1.782 20.769 0.089 -0.22109 0.12409 -0.47933 0.03715
肩宽弧方差 假设方差相等 0.947 0.332 -2.764 145 0.006 -0.66047 0.23899 -1.13282 -0.18812
假设方差不相等 -3.806 19.710 0.001 -0.66047 0.17352 -1.02277 -0.29817
臂根围方差 假设方差相等 1.003 0.318 -1.298 145 0.196 -0.23165 0.17840 -0.58425 0.12095
假设方差不相等 -1.595 17.899 0.128 -0.23165 0.14523 -0.53689 0.07359
全臂长方差 假设方差相等 7.519 0.007 -0.858 145 0.392 -0.19361 0.22557 -0.63944 0.25222
假设方差不相等 -1.602 30.602 0.119 -0.19361 0.12082 -0.44016 0.05294
表4、表5、表6显示的是情况2、情况3、情况4的数据分别与情况1的数据进行两个样本的独立T检验的结果。在假设方差相等行中,显著值大于0.05,可以视为方差是相等的,考察此行的结果,否则考察假设方差不相等行中的结果;双侧检验差异显著性水平大于0.05时,表明两种情况下的数据无显著差异,大于0.01时,表明有显著差异,小于0.01时,有极显著差异。
表4中双侧检验差异显著性水平均大于0.05,表明溜肩体型与肩部常体左肩高方差、右肩高方差、肩宽直方差、肩宽弧方差、臂根围方差、全臂长方差均没有显著性差异,也就是说两种情况下测量的数据波动情况相似,溜肩体型并没有造成与肩点相关的尺寸测量更不准确。观察表5中双侧检验差异显著性水平,可以发现平肩体型和肩部常体两种情况下左肩高方差、右肩高方差存在极显著差异,肩宽弧方差存在显著差异,肩宽直方差、臂根围方差、全臂长方差不存在显著差异。左肩高和右肩高的测量在第1种和第3种情况下数据差异非常大,肩宽弧的测量数据差异较大,这说明平肩体型的被测者在测量左肩高、右肩高、肩宽弧时较肩部常体准确性低。表6结果显示冲肩体型与肩部常体肩宽弧方差存在极显著差异,左肩高方差、右肩高方差存在显著差异,这表明冲肩体型情况下肩宽弧、左肩高、右肩高数据获取难度较肩部常体大,其中肩宽弧数据获取难度程度更大。
表4、表5、表6的结果表明溜肩体型对肩点相关的6个尺寸的获取没有很大影响;平肩体型和冲肩体型情况下左肩高、右肩高、肩宽弧测量数据波动性更大,测量数据不准确性增加,而另3个部位尺寸数据不受不同肩部情况的影响。综合所有分析结果表明平肩和冲肩的情况会影响肩点的获取,使得肩点获取更加困难,溜肩情况对肩点获取的影响较小。左肩高、右肩高、肩宽弧的尺寸和肩点的关联度高,这3个尺寸的测量基准点只有肩点,肩点获取准确性直接影响测量结果准确性;臂根围和全臂长由多个测量基准点控制,因此肩点获取是否准确对其测量结果影响较小;肩宽直尺寸的测量基准点只有肩点,但当肩点小范围上下移动时肩点所处的水平位置发生的偏移较竖直位置发生的偏移小,因此肩宽直尺寸受肩点获取情况影响小,不同情况下数据获取准确性差异不大。溜肩和平肩都是肩斜度不同于常体肩部,溜肩状态下肩斜线角度大,肩点的判断较容易,因此溜肩对肩点获取影响小;而平肩状态下肩斜度角度小,肩点判断较困难,导致平肩对肩点获取影响大。冲肩状态下两肩点往前,肩斜线不易观察,在测量时从人体前方和侧面获取肩点时会受冲肩肩部形态的影响,因此冲肩对肩点的获取影响大。
2.5 实验结论
溜肩体型左肩高、右肩高、肩宽直、肩宽弧、臂根围、全臂长尺寸数据测量波动性和肩部常体尺寸差异很小,溜肩体型对肩点获取影响很小。平肩体型左肩高、右肩高、肩宽弧尺寸数据测量波动性较肩部常体尺寸大,且存在显著差异,而肩宽直、臂根围、全臂长尺寸数据测量波动性和肩部常体尺寸差异很小,平肩体型对肩点获取影响较大。冲肩体型左肩高、右肩高、肩宽弧尺寸数据测量波动性较肩部常体尺寸大,且存在显著差异,而肩宽直、臂根围、全臂长尺寸数据测量波动性和肩部常体尺寸差异很小,冲肩体型对肩点获取影响较大。
3 总结与展望
服装用人体测量实验过程中影响测量结果准确性的因素有很多,如环境因素、心理因素、技能水平、测量路径等等。此次我们以不同肩部形态下肩点的获取情况为出发点,研究了溜肩、平肩、冲肩情况对肩点获取的影响。实验结果表明,溜肩情况对肩点获取的影响不明显,平肩和冲肩情况对肩点获取的影响较显著。在人体测量时,测量者需要对平肩体型和冲肩体型的肩点位置判断更加细心,以减少肩部形态对肩点获取的影响,同时需要增加其他测量尺寸来提高测量的准确性,例如从人体前方测量两个肩点的水平弧长,左右肩点的前冲量,这些尺寸的增测也提高了服装样版制作的准确性[11-12]。
服用人体测量作为获取人体尺寸的重要途径之一[13],其尺寸获取的准确性相当重要,对于样版绘制、服装制作以及数据分析都有很大影响[14-15]。在安排测量实验时应尽量减小系统误差,提高数据测量准确性。非接触式人体测量发展迅速,在判断非接触式测量数据准确性时需要和手工测量数据进行比对,因此提高手工测量数据准确性是非常必要的。
参考文献
[1]SHANG Xiaomei, XING Xiaoyu, GAO Peipei. Hierarchical Analysis Method and Model Based Data of Controlling Parts of the Body for Clothing[J]. Journal of Fiber Bioengineering and Informatics, 2014,7(4):479-494.
[2]HONG Zhenglin, LI Pengwei, SHANG Xiaomei. Psychological Factors Affect Measured Data of Human Body[J]. Textile Bioengineering and Informatics Symposium Proceedings, 2015:122-127.
[3]中华人民共和国国家质量监督检验检疫总局,中国国家标准化管理委员会.GB/T 16160-2008 服装用人体测量的部位和方法[S].中国标准出版社,2008.
[4]王晓云,单毓馥. 服装垫肩的设计研究[J]. 纺织学报,2007(07):94-97.
[5]彭磊,谢红,邹奇芝,等.基于量身定制特体女装原型样板的生成[J].纺织学报,2011, 32(4)101-105.
[6]李晓志,李晓久. 基于部位划分的三维人体曲面模型的构建[J]. 纺织学报,2013(09):145-149.
[7]张金花,王宏付. 基于三维人体测量的女性肩部研究[J]. 纺织学报,2011(05):95-97.
[8]王凤丽. 肩斜度的结构平衡[J]. 国际纺织导报,2005(02):82-83+66.
[9]沈璐.基于特殊体型的纸样调整[J].天津纺织科技2012(03):38-40.
[10]潘春宇,吕吉,梁惠娥,等. 女上体肩斜度测量与其反三角函数推演[J]. 纺织科技进展,2011(06):69-72.
[11]金晶,罗晓菊,贺文娟. 女装肩部造型与结构相关性研究[J]. 现代纺织技术,2010(06):12-14.
[12]王祺明,张渭源. 服装产业用人体测量基准点的比较研究[J]. 江苏纺织,2006(12):39-41.
[13]黄灿艺. 服装样板肩斜推档研究[J]. 针织工业,2010(09):57-59.
[14]于晓景. 肩袖造型设计—浅谈女装肩袖部位结构配比关系[J].东华大学学报:社会科学版,2012,12(4):241-245, 251.
[15]李钊,占玥,张文斌,等. 基于东华原型袖窿曲线变化的相关因子分析[J]. 天津工业大学学报,2011,30(5):30-34.
Study on the Influence of Human Shoulder Morphology on the Acquisition of Acromion Points
HONG Zheng-lin2 LE Yi-meng2 WU Shang1 SGANG Xiao-mei 1
(1. College of Textile and Clothing Engineering, Soochow University, Suzhou Jiangsu 215021,China
2 .Leacheng Apparel Co.,Ltd, Suzhou Jiangsu 214426,China)
Abstract: As three-dimensional measurement reference points, acromion points are influenced by several aspects in their accuracy of judgment. This paper mainly studies the influence of different human shoulder morphology on the acquisition of acromion points. The accurate acquisition of acromion points can be judged by the fluctuation of the measured data which are relevant to acromion points. 230 subjects participated in this body measurement experiment. By analyzing the data of the left shoulder height, the right shoulder height, the straight shoulder width, the shoulder width, the armscye girth and the arm length, it is found that the shoulder slope doesnt influence the acquisition of acromion points significantly, while the forward shoulder does, which leads to the incorrect measurement of the data.
Key Words: anthropometry; shoulder morphology; shoulder slope; acromion points
(责任编辑 竺小恩)

