钢筋混凝土简支梁非线性分析

张琦 刘富宙

摘 要：文章应用不同的有限元建模方式，对钢筋混凝土梁进行了非线性分析，结果发现不同的建模方式对结果影响很小，但是对计算效率影响很大，在实际应用过程中，选择合理的模型单元和计算方法对结果影响很大。

关键词：混凝土；非线性分析；有限元

一、问题描述

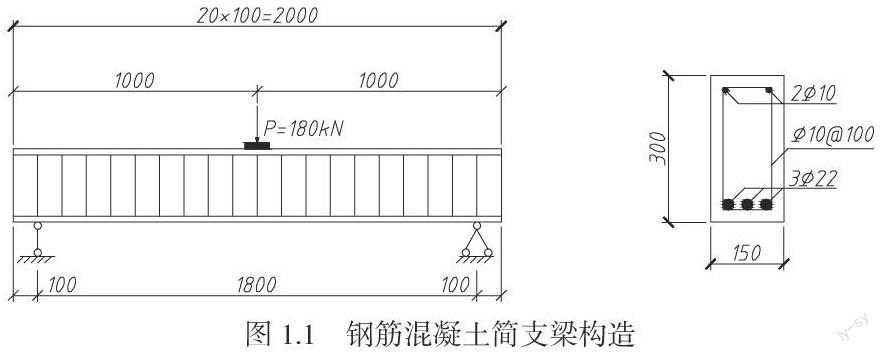
钢筋混凝土简支梁，梁的跨度为L=2.0m，横截面为矩形，尺寸为b×h=150mm×300mm，支座范围100mm，净跨度为1800mm。梁内受拉纵筋采用3φ2，架立筋采用2φ10，箍筋采用φ10@100，钢筋保护层厚度为30mm。混凝土采用C30，钢筋全部采用HRB335。跨中集中荷载P作用于一刚性垫板，垫板尺寸为150mm×300mm。

二、分离式建模分析

（一）模型与单元

建立分离式有限元，混凝土采用SOLID65单元，钢筋采用LINK8单元，不考虑钢筋混凝土之间的粘结滑移。创建分离式模型时，将几何实体以钢筋位置切分，划分网格时将实体的边线定义为钢筋即可。加载点以均布荷载近似代替钢垫板，支座处则采用线性约束。考虑模型的对称性，创建1/4模型。单元尺寸以50mm左右为宜。

（二）材料性质

采用《钢筋混凝土结构设计规范》（GB50010-2010）规定的强度设计值。

1.混凝土材料

混凝土立方体抗压强度标准值fcu，k=30MPa，单轴抗压强度fc=14.3MPa，单轴抗拉强度ft=1.43MPa，张开裂缝的剪力传递系数βt=0.5，闭合裂缝传递系数βt=0.95，弹性模量Ec=3×104MPa，泊松比υc=0.2，拉应力释放系数采用缺省值Tc=0.6。

混凝土本构关系采用《钢筋混凝土结构设计规范》（GB50010-2010）建议的应力-应变关系，数学表达式为：

按照规范计算和规定可分别求得n=2，ε0=0.002，εcu=0.0033，上述曲线可用一系列数据拟合以便于输入，此处采用多线性等向强化模型MISO模拟。

（2）钢筋的屈服强度fy=300MPa，弹性模量Es=2.0× 105MPa，泊松比υs=0.3。采用双线性等向强化模型BISO模拟。

（三）有限元建模

考虑到模型的对称性，创建1/4模型。三个轴向的尺寸分别为75，300，1000。在钢筋位置进行切分。通过循环切分，切出箍筋位置，拟加载面，拉区钢筋竖向位置，压区钢筋竖向位置，钢筋水平位置，单元尺寸取50mm。

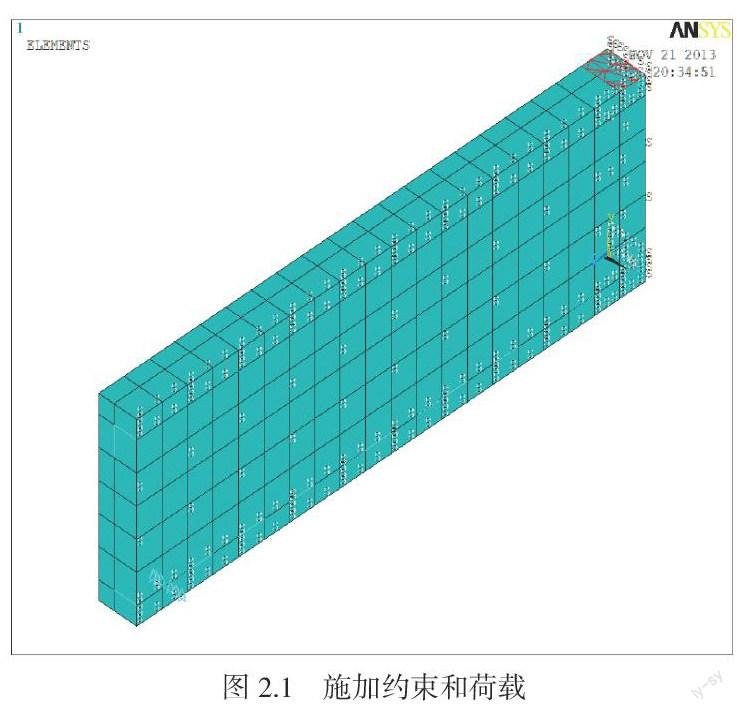
加载点以均布荷载近似代替钢垫板，即在垫板处施加12N/mm2的均布荷载，支座处采用线约束。跨中对称面和水平对称面都施加对称约束。施加约束和载荷之后的模型如图 2.1所示。

计算方法选择牛拉法，收敛准则采用位移收敛准则，收敛误差设为1.5%。

（四）分析结果

计算得到简支梁跨中截面荷载位移曲线，如图 2.2所示。

极限荷载为172.156KN，最大竖向变形为11.0541mm，屈服荷载为168.356KN，屈服时跨中竖向变形为5.60643mm。由于采用牛拉法，无法捕捉到下降段，因而计算结果没有出现下降段。

三、整体式建模分析

将钢筋连续均匀分布于整个单元中，通过计算钢筋的体积率考虑混凝土与钢筋对刚度的贡献，单元仅为SOLID65。选取的材料本构关系、网格划分、施加荷载和约束与分离式建模相同。

计算得到的荷载位移曲线如图 3.1所示

极限荷载为176.034KN，最大竖向变形为8.65513mm，屈服到破坏的时间很短，屈服荷载为172.069KN，屈服时的竖向变形为5.6668mm。

四、手算分析

参考《混凝土结构基本原理》计算跨中荷载位移曲线如图 4.1所示。计算采用的混凝土本构关系，钢筋本构关系与有限元分析相同，所得的极限承载力为138KN，最大竖向变形为7.08mm。

五、比较分析

由于未找到相关的试验数据，所以采用手算的方式进行验证。计算中发现被分析的构件属于超筋梁，钢筋在混凝土壓碎前都没有发生屈服。

比较发现，建模方式对结果的影响很小，但是整体式建模计算收敛速度要快得多。

手算结果比有限元分析结果要保守的多，且没有明显的延性段，与超筋梁实际破坏形态接近。

综合分析，有限元模拟可以很好的考虑材料的非线性，但是在实际应用过程中，选择合理的模型单元和计算方法对结果影响很大。