服装集装箱装箱优化研究

马芳婷 俞晓琳 吴雯

（嘉兴学院，浙江 嘉兴 314200）

【摘 要】物流运输在企业发展中的地位越来越重要，提高决策和运作效率能给企业带来更大的利润空间。针对传统高档服装吊挂集装箱在装箱时仅凭经验选择横、纵支撑杆排列方式的现象，文章采用线性规划法对吊挂集装箱进行装箱优化研究。在考虑各种现实约束条件的情况下，建立优化模型，通过求解并设计相应的管理应用程序，能较快得出服装装箱的最优件数和装箱方案，为吊挂运输的服装在装箱时提供借鉴。

【关键词】吊挂集装箱；装箱优化；模型

【中图分类号】U169 【文献标识码】A 【文章编号】1674-0688（2016）06-0152-04

0 引言

现代物流业是20世纪90年代在现代管理技术和信息技术的基础上发展起来的新兴产业。它是以服务社会为第一目标，以实现企业整体最优为目的，以信息为中心的商品供应体系，被称为“第三方利润源”。随着经济全球化的不断发展，生产、贸易、资本的全球化带来物流活动的国际化，而国际物流很重要的一种运输方式就是海上运输，其中以集装箱为装货容器的就占了很大一部分。2014年，在全球10大集装箱港吞吐量排行榜上，中国港口占了7席。2014年，我国集装箱吞吐量突破2亿标箱大关，据中港网数据集装箱吞吐量从1亿标箱到2亿标箱，跨时仅7年。然而，在其高速发展的背后存在着很大的问题，2014年物流成本占GDP的比重为17.8%，2015年占18%，仍徘徊在较高水平。物流成本的居高不下降低了企业的效益，制约了物流业的发展。其中，集装箱的不合理装箱就是一个重要的影响因素。而且，集装箱装载问题广泛存在于工业生产、服装行业及现实生活中的包装等领域，對装载问题的研究日趋广泛而重要。就服装集装箱的装箱问题而言，以标准的服装集装箱为典型，当前服装企业在集装箱装箱过程中，针对不同型号和货物数量的订单，往往根据自己的相关经验或感觉来做出产品或项目的决策方案，与现代企业管理要求的“科学决策”相去甚远[1]。在货物较多的时候，不可避免地造成集装箱利用率低下，增加了物流成本。而随着社会经济的发展，高档服装客户的比例在不断增加，目前在外贸服装物流中，挂输运输已经成为一种趋势。因此，实现高档服装吊挂集装箱装载的优化，成为我们研究的课题。

本课题针对高档服装吊挂集装箱装载的优化问题进行研究。为企业提供能够快速得出是选择横向还是纵向支撑杆的决策工具，即高档服装吊挂集装箱装箱决策软件包，提高企业装箱效率与集装箱的空间利用率，降低物流成本，提高经济效益，增强企业的竞争力；促进集装箱装箱的合理化，降低整体物流成本，优化物流系统；取得一定的社会效益，节约资源，有利于可持续发展。

集装箱装箱优化问题通常是指把货物按照一定的规则装入集装箱，在既定的约束条件上，研究合理的装箱方案，使得集装箱的空间利用率最大化。集装箱装箱问题可追溯到1831年高斯研究布局问题。自从新西兰学者George J.A和Robinson D.E[2]在其所著的文章中提出了关于集装箱装载问题的启发式算法后，此后许多专家学者都从不同的角度使用启发式算法对集装箱装箱优化提出了自己的解决方案。Chen[3]针对一般的集装箱装载问题，从数学角度出发，给出了0-1整数规划模型。Ivancic[4]等人提出了基于整数规划的三维装箱启发式算法，此算法仅适用于同种规格的货物。但是，由于启发式算法得出的解与最优解的差异难以评价，近年来人工智能算法包括模拟退火算法、遗传算法与禁忌搜索算法等的研究越来越多。三维装箱问题包括条带装载问题（3D-SPP）[5]、箱柜装载问题（3D-BPP）[6]。依据容器的垂直截面将系列长方体物品装入，使得装入容器的装载长度最小。对高档服装的吊挂装箱优化研究具有借鉴意义。

国内集装箱装箱问题的研究开始于20世纪末，许多专家学者提出了新的观点与方法。卜雷[7]用改进遗传算法（考虑货物放置方向、容积、质量重心等，也调整了目标函数）优化铁路集装箱单箱三维装箱问题。乐千桤采用三维空间分割策略，在三维问题上进行更深入的优化分析[8]。此外，一种新兴的随机优化算法——分布估算法[9]，也在多个领域得到应用，对于利用率的优化上已取得多个成果应用[10]。但是，对于集装箱装箱问题还是有很大的空间可以让我们去深入研究。

本课题主要针对如何使相同积载因数的货物（轻泡货）在单个集装箱内满足集装箱最大载货量的情况下，装货量达到最大（现仅研究横向或纵向的支撑杆排列方式对仓容量的影响，不考虑支撑杆的载重量，集装箱运输的稳定性等），建立装载问题的数学模型，求区域内的最优解，增强服装装箱方案的实用性。

1 吊挂集装箱装箱问题概述

1.1 装箱问题简介

集装箱装载问题是一个具有复杂约束条件的组合优化问题，是理论上的NP-hard问题。所谓组合化，是指在离散的，有限的数学结构上，寻找一个满足给定条件，并使其目标函数值达到最大或最小的解。组合优化问题通常带有大量的局部限制点，往往是不可微的、不连续的、多维的、有约束条件的。高档服装吊挂集装箱的装载问题在于如何选择横向支撑杆和纵向支撑杆，使得空间利用率最大。

德国的Dyckhoff H.[11]提出依据集装箱数量把装载问题分为多集装箱装载和单集装箱装载。给定一组货物，前者要求货物必须完全装入，以所需集装箱数量最少为目标；后者允许货物有剩余，以装入集装箱的总体积（或体积与载重量的总利用率）最大为目标。Bortfeldt A.提出按待装载的货物将装载问题划分成3类。

货物的规格完全相同，即单一尺寸的货物填装问题，这类问题被称为“同类”（homogencous）问题；货物有不同类型，这类问题被称为“强异”（strongly heterogenous）问题；货物只有少数几种不同的类型，但每类货物具有一定的数量，这类问题被称为“弱异类”（weakly hetergengrous）问题。

本文研究的吊挂集装箱装载问题属于“同类”问题。

1.2 线性规划算法在转载问题中的应用

在现有的文献中已有利用整数线性规划方法解决集装箱装载问题的例子。Ivancic等人给出了一种基于整数规划的启发式算法，依次将货物装入集装箱内，此算法仅适用于同种规格的集装箱装配，且随着货物数量的增多，变量和约束条件急剧增加，使问题越来越难求解。Michael Eley [12]采用同时性策略，设计了一种基于整数规划的多容器集装箱装载问题算法[13]，在空间利用率特别是强多种类型物品问题上，表现很好。在稳定性和重量分布方面也有较好的结果。

1.3 数学模型建立

本文所建立的模型如图1所示，装箱问题的目标函数为最大化集装箱的空间利用率，由于集装箱的容积固定，所以在保证减少高档服装的货损前提下，最大化空间利用率，即最大化装入货物的体积，如公式（1）和公式（2）。

MAXF（A）=（w×h×l）/[（a+a1）×（c+c1）×b]（1）

∑（c+c1）≤h

∑（a+a1）≤w

∑b≤l

∑m≤M

MAXF（B）=（w×h×l）/[（a+a1）×（c+c1）×b]（2）

∑（c+c1）≤h

∑（a+a1）≤l

∑b≤w

∑m≤M

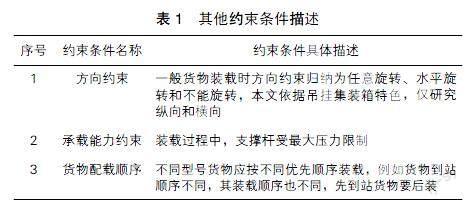
式中：F表示目标函数，M表示净载重，m表示单件衣重，a表示单件衣宽，a1表示x轴上的横向排列衣服间距，（a+a1）表示虚拟衣宽，b表示单件衣厚，c表示单件衣长，c1表示y轴上的纵向排列衣服间距， （c+c1）表示虚拟衣长，W、l、h表示吊挂集裝箱内部长度、宽度、高度尺寸。以上的目标函数及约束条件是对装载过程中货物空间布局的约束，在实际装载过程中，仅在以上约束的限制下将以上目标函数作为唯一目标是不够的，还需要考虑多方面的条件约束。其他约束条件见表1。

2 算例分析

此项高档服装吊挂决策主要针对如何使用相同积载因数的货物（轻泡货）在单个集装箱内，实现装载量最大（现仅研究横向和纵向的支撑杆排列方式对仓储容量的影响，不考虑支撑杆的承重量和集装箱运输稳定性）。

决策界面中需要输入的数据包括需吊挂运输的服装尺寸（包括厚度）、衣服净重、衣长间距、衣宽间距、集装箱内部尺寸及承重量。

衣服的尺寸是软件进行运算的重要参数，包括衣长、衣宽，此外还需要测量厚度，其中衣厚的测量上可能会存在一定的难度，高档服装中西装的厚度为肩的厚度，高级礼服的厚度需要考虑衣身最大厚度。其余数据则是根据企业自己的要求而设置衣宽间距、衣长间距、衣厚间距。高档服装集装箱决策软件输入界面图如图2所示。

通过决策软件应用分别得出纵向、横向支撑杆的最大挂装件数，如图3所示，比较纵向、横向的最大挂装件数后，选择其中较优的方案。以图1数据为例，A型排列支撑杆可在x轴坐标轴上放4件，y轴上放73件，z轴上为2层，最大装载件数为584；B型排列支撑杆可在x轴上放29件，y轴上放12件，z轴上为2层，最大装载件数为696，因此决策结果为选择B型排列支撑杆。表2和表3分别为横向、纵向支撑杆排列方式的算例。

3 结语

本文阐述了集装箱装载问题的重要性，在经济领域中的战略地位。以高档服装吊挂集装箱装箱优化为研究对象，在阅读国内外文献基础上，重点分析了线性规划算法。利用该算法使得在高档服装进行挂式装箱时，所选择的支撑杆排列方式有理论依据。并根据该算法原理设置运行参数，设计出高档服装吊挂集装箱决策程序软件包，使之在面对装箱业务时能快速、直接地给出装箱方案。

本文对高档服装吊挂集装箱装箱优化进行了研究，通过对理论知识的学习以及对前人算法的研究，应用基于线性规划的算法求解吊挂集装箱装箱问题，取得了一定的研究成果。但由于该领域的应用背景和所涉及的学科知识都非常广泛，本文的研究内容仅是吊挂集装箱装载问题的冰山一角，还有许多问题，例如改善集装箱架体结构等需要在今后的研究中加以解决。

（1）本文研究的是单吊挂集装箱装载问题，目标函数是箱体的空间利用率最高，但当需挂式集装的服装数量很多需要多个集装箱来共同装载，这时的目标函数还应包括所用的集装箱数量最少。

（2）本文仅考虑了高档服装挂式装载中的典型约束，并没有考虑实际装载过程中的特定约束条件，如货物运往不同目的地时先后的装填顺序，在高档服装吊挂集装箱中纵横支撑杆的结合是否比单一的横向或纵向支撑杆更能提高空间利用率，以及在考虑支撑杆的载重量时对横纵支撑杆选择的影响等。

（3）吊挂集装箱横纵支撑杆选择的求解方法还存在非常广阔的研究空间，可以有以下研究方向：针对各种现有求解算法的优点和缺点，将2种及以上求解算法综合以弥补单一算法的不足。随着新的优化技术或优化工具的出现，改变运算策略，增添运行参数使实验模拟更符合实际装载情境。

参 考 文 献

[1]袁捷敏.透析我国民营企业家的管理缺陷[J].企业科技与发展，2008（24）：52-53.

[2]Martello S，Pisinger D，Vigo D.The Three-Dimen-

sional Bin Packing Problem[J].Operations Research，2000，48：256-267.

[3]David Pisinger.Heuristics for the container loading

problem[J].European Journal of Operational Pese-

arch，2002，141：382-392.

[4]Michael Eley.Solving container loading problems by block arrangement[J].European Journal of Opera-

tional Research，2002，141：393-409.

[5]Bortfeldt A，Mark D.A heuristic for the three——dimensional strip packing Problem[J].European journal of Operational Research，2007，183（3）：267-1279.

[6]Bortfeldt A.A hybrid algorithm for the capacitated

vchicle routing problem with three—dimensional loading constraints[J].Computers & Operations Re-

search，2012，39（9）：2248-2257.

[7]卜雷，袁新江，蒲云.基于遺传算法的集装箱单箱三维装载优化问题[J].中国铁道科学，2004，25（4）：108-111.

[8]乐千桤，陆鑫，孙全力.基于组合模块的装箱优化算法的研究[J].实验科学与技术，2006（1），38-40.

[9]高尚，武器.目标分配问题的分布估计算法和参数设计[J].东南大学学报（自然科学版），2012，42：178-181.

[10]樊玮，苏秋波.基于分布估计算法多行段座位分配模型，信息与控制，2012，41（6）：774-778.

[11]郭贝贝.复杂集装箱装载问题研究及可视化实现[D].大连：大连海事大学，2009.

[12]沈秀敏.基于整数线性规划方法的集装箱装载布局优化[D].大连：大连海事大学，2013：32-33.

[13]葛立臣，权明伍.集装箱力转设备架体结构优化[D].辽源：辽源职业技术学院，2014.

[责任编辑：陈泽琦]

【基金项目】本文系嘉兴学院重点SRT资助项目“嘉兴学院大学生研究训练（SRT）计划”（项目编号：851715027）。

【作者简介】马芳婷，女，浙江绍兴人，就读于嘉兴学院物流管理专业；俞晓琳，女，浙江杭州人，就读于嘉兴学院物流管理专业；吴雯，女，浙江嘉兴人，就读于嘉兴学院物流管理专业。