基于Zigzag块扫描的光栅化算法设计与实现

聂瞾 田泽 马城城

摘 要：光栅化是图形处理器的关键单元，实现几何图元到片段的转换，其功能、性能决定了图形处理器的优劣。传统的光栅化方法大多采用线扫描方式，利用线填充算法在水平或竖直方向填充像素，计算过程复杂、资源占用量大，不适用于对硬件资源与芯片面积有极大限制的嵌入式图形处理器设计。文中在分析Zigzag扫描原理的基础上，提出一种基于Ziazag块扫描的光栅化算法，该算法计算过程简练、资源消耗少。通过算法仿真平台的验证，功能正确、性能较传统线扫描算法提升30%以上、资源占用大大降低，满足图形处理器设计要求。

关键词：光栅化；块扫描；Zigzag扫描

中图分类号：TP301 文献标识码：A

在图形应用快速发展的背景下，复杂的3D图形应用需求与日俱增。图形处理器（Graphic Processing Unit，GPU）作为显示系统的核心，以硬件加速的形式实现了3D图形绘制，其功能、性能直接决定了图形绘制的质量和速度，在计算机系统中的作用日益提高。

光栅化作为图形处理器的关键单元，是将几何图元转换为片段的重要过程，决定图形绘制的效率和效果，是影响图形处理器功能、性能的重要因素。传统光栅化单元大多采用线扫描实现，如：Bresenham算法、DDA算法等，此类算法实现需占用大量运算资源和较多的存储资源[ 1 ]。然而，嵌入式图形处理器设计对硬件资源与芯片面积都有着极大的限制要求。基于块扫描的光栅化方法应运而生，块扫描光栅化将几何图元分割成以块为单元的集合，以块为单位进行像素处理，充分利用了图形数据的局部性原理，大大提高了像素生成和处理效率。

Zigzag是一种应用广泛的块扫描算法，本文在分析Zigzag扫描算法基础上，提出一种基于Zigzag块扫描的光栅化算法，结合Zigzag扫描原理，自下向上“Z”型扫描图元，利用块顶点的边界函数判断当前块与图元的关系，完成竖直方向上的Zigzag块光栅化。在实现中，利用边函数的线性变换规律，通过的加、减等简单运算快速迭代计算块顶点的边界函数值，减低计算复杂度，大大提高了光栅化效率。

1 ZigZag块扫描分析

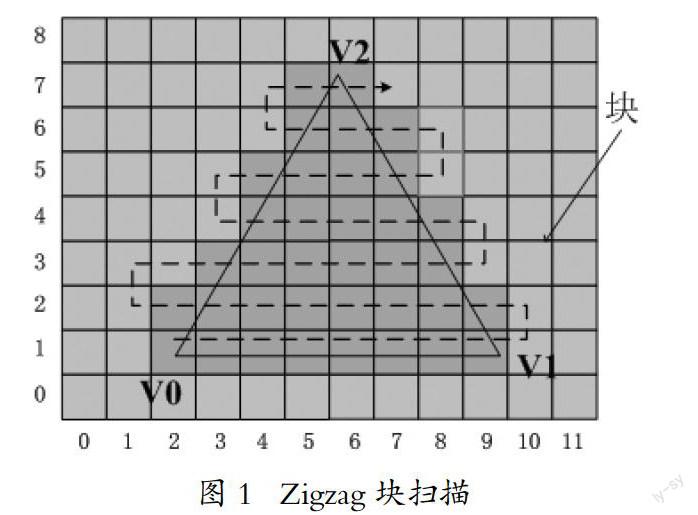
Zigzag是一种全面、高效的图元扫描算法，计算原理明晰，实现简单，广泛应用于现代图形处理器光栅化单元中[ 2 ]。Zigzag块扫描以像素块为单位进行扫描，在y轴方向上从低到高以“Z”字型向上扫描。如图1所示。

Zigzag扫描首先从底部的起始块出发，水平扫描当前行，直到遇到第1个完全在三角形外的像素块，然后Y坐标增加一个像素块高度，反向扫描当前像素块行，依此方式反复扫描，直到扫描线的Y轴坐标大于等于终止位置的Y轴坐标，且扫描状态由发现与三角形相交的像素块过渡到发现完全在三角形外的像素块为止[ 3 ]。

在扫描过程中，当前块与三角形关系确定了扫描的进行方式。具体而言，在水平方向扫描时，如果当前块与三角形有重叠，则向正方向继续扫描，如果当前块与三角形没有重叠则需要结合当前行扫描状态决定是否向上移一行继续扫描；如果遇到第一个完全在外的块且本行已有重叠块的情况下，说明该行已扫描完成应该向上移一行继续反方向扫描；如果在没有重叠块的情况下遇到完全在外的块，则说明正方向上没有重叠快，应该向本行的负方向扫描。竖直方向仅检测当前扫描行与终止位置的Y轴坐标的关系，若大于则扫描结束，若不大于则进行该行水平方向扫描。

2 基于Zigzag块扫描的光栅化算法设计与实现

基于ZigZag块的光栅化扫描算法包含4个处理环节，分别为图元预处理、Zigzag扫描、块与图元位置关系判断和片段生成。图元预处理主要进行对几何图元顶点的存储；Zigzag扫描完成控制参数计算、扫描控制、块参数生成；块与图元位置关系判断完成块与图元位置关系的计算，决定Zigzag扫描路径，生成有效块数据；片段生成负责生成片段并对其属性进行插值。其中，图元预处理和片段生成属于上下文操作，由算法仿真平台负责管理。文本主要讨论Zigzag扫描和位置关系判断两大部分。

2.1 Zigzag块扫描设计与实现

Zigzag块扫描实现对覆盖图元的块的遍历，利用沿竖直方向的“Z”型扫描完成块的遍历。算法包括预处理信息计算和扫描控制2个步骤：

1）预处理计算：包括竖直方向起始、终止点计算，扫描起始点确定和初始水平扫描方向计算4部分。在预处理过程中，计算三角形顶点中y值最大值与最小值，则竖直方向起始值为y值最小值，终止点为y值最大值；扫描起始点为y值最小的顶点的坐标；初始水平扫描方向与扫描起始点指向三角形中间顶点的方向一致。

2）扫描控制：负责进行竖直和水平方向扫描的条件判断，依靠当前块与三角形的位置关系，如果水平方向没有遇到完全在外的块，则应继续水平方向扫描，若遇到则说明当前行扫描完毕应向上移动一行。

根据对Zigzag块扫描的分析，采用模块化设计思路，建立预处理计算模块和扫描控制模块。预处理计算模块根据三角形顶点的坐标信息，找出顶点中y值的最小值与最大值，计算竖直扫描起始和终止坐标，同时确定扫描起始点位置和初始扫描方向。扫描控制模块由控制信息管理、块数据生成和块与图元关系判断三部分组成。控制信息管理负责边函数的计算和递推值的存储，控制边函数信息的管理；块数據生成完成以当前顶点为左下角的块数据生成，递推计算块其余3个顶点的边函数便于位置关系的判断；块与图元位置关系判断根据块4个顶点的12个边函数综合判断确定块与图元的关系，如果块与图元由重叠则需要下发像素块并更新当前顶点，如果没有重叠则需要上移扫描行同时更新当前顶点。

2.2 块与图元位置关系判断

块与图元位置关系判断采用边函数技术，通过块的4个顶点数据生成12个边函数值，利用区域分类确定三种块与图元位置关系，块完全在图元内、块部分在图元内和块在图元外。

边函数是20世纪80年代出现的一种在2D平面内判断点与直线关系的函数，它利用给定的直线将空间划分为3个区域，直线之上，直线之下和直线内[ 4，5 ]。

假定直线从点（x0，y0）到点（x1，y1），法线方向为n=（a，b），则边函数e（x，y）为公式（1），其中a=y0-y1；b= x1-x0；c= x0y1-x1y0。

e（x，y）=ax+by+c公式（1）

若边函数小于0，说明点在法线正区域，既就是点在直线上；若边函数大于0，说明点在法线负区域，既就是点在直线下；若边函数为0，说明点在线内包括在线的延长线上。

相似的，可以利用三角形3边的边函数值确定点与三角形的位置关系，判断条件如下：

1）如果3个边界函数中至少存在一个小于0的值，则点在三角形外；

2）除去A的情况，则点要么在三角形内要么在三角形边上，均认为点在三角形内。更进一步，由于块与三角形的位置关系有完全在内、部分在内和完全在外。

因此，我们可以利用块的4个顶点的边函数综合计算得到块与三角形的位置关系，判断条件如下：

1）如果块的4个顶点均在三角形内部，则当前块与三角形关系为完全在内；

2）如果块的4个顶点均在三角形外部，则块在三角形外；

3）除去1与2的情况，剩余所有块均为部分在内，部分在外。

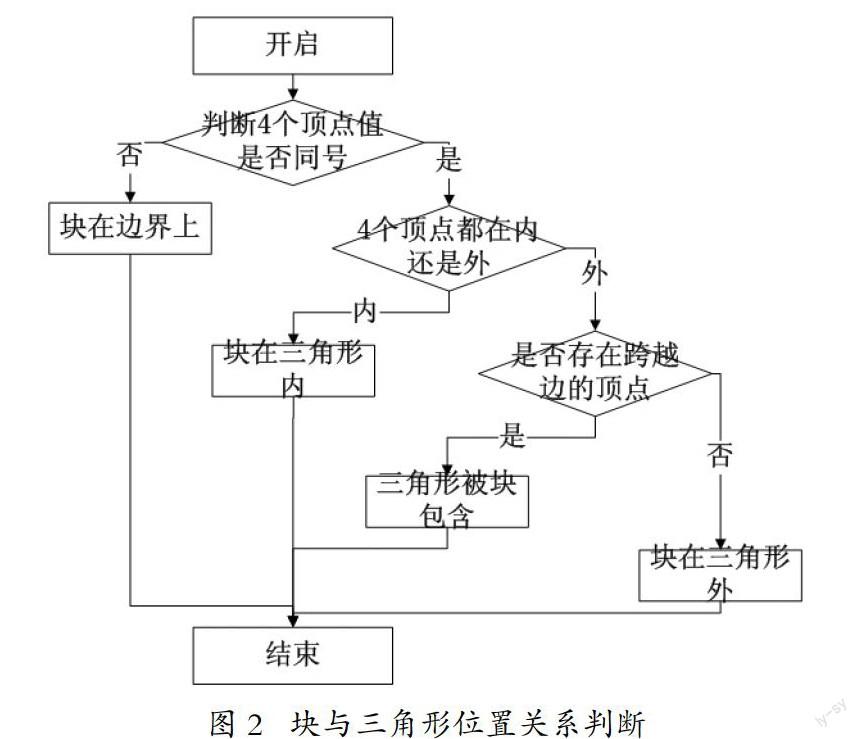
根据以上的分析，设计实现中块与图元位置关系判断的流程如图2所示：

在判断位置关系时，需要先对4个顶点的边界函数值符号进行判断，如果符号同号说明4个顶点要么均在三角形内要么全部在外，此时需要进一步判断。

反之，可以确定块与三角形位置为相交关系即块部分在三角形内部分在外。对于同号可以分为2种情况，同在内部和同在外部，如果4个顶点均在三角形内部那么块一定在三角形内部，反之，则需要进一步判断。

3 算法验证

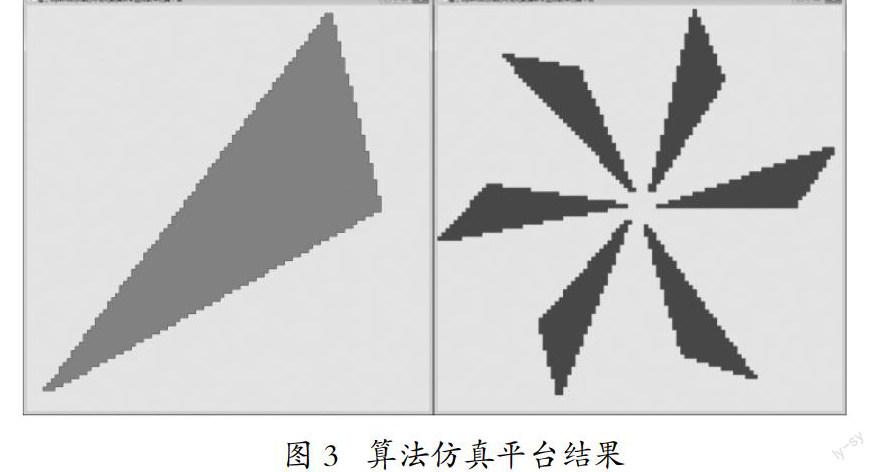
为了验证块扫描光栅化算法的正确性，在算法仿真平台上绘制一个逆时针方向的红色三角形，如图3所示。此外，为了进一步验证在各个方向和不同起始位置的条件，绘制一个通过旋转而成的由6个三角形组成的图案。通过与Windows平台的比较，利用块扫描光栅化算法的绘制结果与Windows结果基本一致，在不同起始位置和方向上，也与Windows平台值，证明块扫描光栅化算法的正确性，达到了预想的效果[ 6 ]。

另一方面，在算法仿真平台上，对基于块扫描和线扫描的三角形图元光栅化算法的性能进行了评估和对比，对于测试中的红色三角形来说，线扫描算法平均需要196.37毫秒，而基于块的扫描平均需要148.31毫秒，对该三角形来说，块扫描技术相对线扫描少使用约48毫秒，效率提升32.4%。由于光栅化单元中三角形参数建立和属性初始化还需要占用一定的时钟时间，会对最终的光栅化性能产生影响，另外不同形状和大小的三角形，由于边界运算和内部像素填充的不同，块扫描算法带来的性能提升存在差异。

4 总结

本文通过对已有图元光栅化算法的研究，着重对Zigzag扫描和边界函数进行深入讨论，提出一种基于块扫描的光栅化算法。该算法利用Zizag原理“Z”型扫描图元，完成自下向上的光栅化。同时，根据块顶点边界函数方法判断块与图元的位置关系，利用块的4个顶点与三角形关系，推导得出块与三角形的位置关系。在设计与实现中，利用边函数的局部性，通过简单的加、减操作快速迭代计算临近点的边函数值，进一步加快判断扫描的速度。在算法仿真平台上的验证，表明块扫描光栅化算法能够快速准确地完成圖元的光栅化，满足图元光栅化的正确性和实时性要求。

参考文献：

[1] 韩俊刚，蒋林，杜慧敏等.一种基于图形加速器和着色器的体系结构[J].计算机辅助设计与图形学报，2010.

[2] Tomas A M，Eric haines，Naty Hoffman. Real-Time Rendering[M].2 Ed.夏文宇，胡艳祥译.北京：清华大学出版社，2000.

[3] 谭显强.基于FPGA的3D图形处理器IP核的设计与实现[D].南京：南京航空航天大学.2010.

[4] 沈陈华.平面上点与多边形包含关系Q算法[J].扬州大学学报，1992，2（4），24.

[5] 张全伙，张剑达.计算机图形学[M].北京：机械工业出版社，2003.

[6] 王润科，张彦丽.判断点与多边形位置关系的算法综述[J].甘肃联合大学学报：自然科学版，2006，20（6）.

作者简介：聂瞾（1991-），男，陕西华县人，硕士研究生，研究方向：计算机科学与技术。

导师简介：田泽，博士，研究员，中国航空工业首席技术专家，研究方向：SoC设计、嵌入式系统设计等。