基于自适应阈值小波变换的心音去噪方法
周克良,邢素林,聂丛楠
(1.江西理工大学电气工程与自动化学院,江西赣州341000;2.江西理工大学机电工程学院,江西赣州341000)
基于自适应阈值小波变换的心音去噪方法
周克良1,邢素林2,聂丛楠2
(1.江西理工大学电气工程与自动化学院,江西赣州341000;2.江西理工大学机电工程学院,江西赣州341000)
摘要:在采集心音信号时,难免会引入一些噪声,对心音信号诊断之前必须对其做去噪处理。由于心音信号是非线性非平稳信号,对心音信号去噪处理常用小波变换去噪方法,但是传统的小波阈值函数去噪方法需要自定义阈值,去噪效果也不理想,且可能会滤除了大量的细节特征,从而无法对心音信号做出正确的判断。为了克服传统小波阈值函数对心音信号去噪处理出现失真的问题,本文在半软阈值函数的基础上提出了基于蚁群算法优化选取阈值的非线性小波变换去噪方法。以原始心音为研究对象,通过选用db6小波并进行6层小波分解,分别选用硬阈值函数、软阈值函数、半软阈值函数、蚁群算法的优化阈值的半软函数等不同的小波去噪处理,并将去噪效果与原始心音进行对比,然后利用蚁群算法的全局搜索性搜索最小均方误差意义下的最佳阈值。仿真结果分析表明:蚁群算法优化选取阈值的心音去噪效果不仅能够去除噪声,还能保留信号细节特征,该方法与传统的硬阈值函数去噪方法相比信号的信噪比(SNR)和均方根误差(RMSE)均得到明显的改善。
关键词:心音去噪;小波变换;自适应阈值;蚁群算法
0引言
传统的心血管疾病的检查依据是借助于心电图、超声心动图以及医生的个人经验进行判断,检测手段比较单一,无法准确地对病患的病情做出快速准确的判断;而心音检测的出现,不仅拓宽了心血管疾病的检测手段,而且由于心音在检测心血管疾病检测中具有无损伤检测特点,所以心音在心血管检测中具有特殊的价值[1-4]。心音信号十分微弱、不稳定、非线性,而且容易被外部环境与人体自身诸多因素影响或干扰,直接影响到心音处理诊断的结果,所以对心音信号的去噪尤为重要。Paulet等[5]提出了改进的基于心电信号的频域最小均方误差(MMSE)估计的心音去噪方法,该方法可以去除白噪声,但是心音信号中的一些细节特征也被滤除。Yuenyong等[6]采用降采样和离散小波阈值去噪,该方法低频噪声无法去除。小波变换时频分析方法,具有时频局部化和多分辨率的特点,不仅可以处理平稳信号,也可以处理非平稳信号。Donoho等[7-8]提出的小波阈值去噪方法是实现最简单、计算量最小的一种方法,因而得到广泛应用。陈远贵等[9]提出一种新的双参可调小波阈值函数,通过调整参数,使信号与噪声间的过渡区更适合于所要分析信号的特性,该方法的心音去噪效果有一定改善。在此基础上,本文提出一种基于蚁群算法的自适应阈值的小波变换心音去噪方法。
1心音信号的小波去噪
1.1心音信号的小波去噪问题
由于心音信号是细微的信号,信噪比低,所以心血信号会与体内存在的大量的噪声融合在一起,无法直观地检测出心音信号,需要通过去噪手段,提取出目标心音信号,以便医生能够做出正确的判断。图1(a)中所示是正常心音信号的S1和S2信号的波形。图1(b)为图1(a)中数据加入一些噪声,模拟出心音信号在噪声中的分辨情况;噪声选取的高斯白噪声,在图1(b)中,心音信号融合在噪声中,很难分辨出心音信号。图1(c)是使用传统的硬阈值函数对含有噪声的心音信号进行去噪后的图形,明显地观察出图形中仍存在比较大的噪声。图1(d)中是使用软阈值对含有噪声的心音信号进行去噪后的图形,与图1(b)相比较,去除了比较多的噪声,但是一些特征也被平滑掉了。本文选择的小波去噪方法根据小波分解的不同层次选取不同的阈值来做阈值处理可以达到更好的去噪效果。

图1 传统阈值函数对心音信号去噪效果图Fig.1 The use of traditional threshold functions of heart sounds denoising effect
1.2离散小波阈值函数去除噪声原理
含有噪声信号模型表示为:
y(t)=x(t)+n(t),
(1)
其中:y(t)表示含噪心音的信号,x(t)表示真实心音信号,n(t)表示高斯白噪声信号。噪声n(t)一般是高斯白噪声。
离散小波函数表示为:
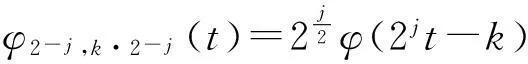
(2)
其中:2-j为尺度因子;k·2-j为平移因子。
相应的离散小波变换表示为:

(3)
其中φ*(t)是φ(t)的复共轭。
离散小波阈值去噪方法:
1)对含有噪声心音y(t)的小波变换计算时,选择比较合适的小波分解层数以及合适的小波基函数,进行小波多层分解得到相应层次的小波分解系数wj,k。
2)对小波分解系数wj,k进行阈值处理。
(4)
其中γ是阈值,wj,k是小波分解系数。
由上可知,心音信号去噪处理的关键性问题是选取最佳的阈值函数以及确定合适的阈值。
2自适应阈值确定
2.1基于最小均方误差的阈值计算
(5)
(6)
其中:wi(t)为离散小波变换系数;γ是阈值。
由离散小波变换分解获得的各分解系数的均方误差计算表达式可表示为:

(7)
由于x(t)和n(t)之间的内积近似为零,简化公式(7)得:
(8)
其中

(9)
式(8)可以分两部分表述:
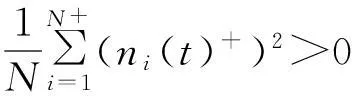

(10)


(11)
噪声方差可以表示为:
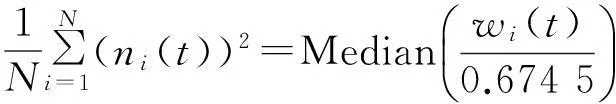
(12)
其中:wi(t)为离散小波变换的分解系数,Median()为求中值函数。不同层次的心音分解系数应该采用不同的最优阈值对其进行阈值处理。本文在最小均方误差意义下利用蚁群算法全局搜索最佳阈值,可以得到更好的去噪效果。
2.2最优阈值函数的选取
本文利用全局搜索能力较好的蚁群算法,搜索阈值函数在最小均方误差MSE(T)条件下,最小时的最优阈值T[10]。蚁群算法优化搜索过程如下:
1)相关参数初始赋值。n代表蚁群算法迭代的次数;m代表蚁群中蚂蚁的数量;ρ表示信息素蒸发系数;τ0代表蚁群算法信息素强度初始值;Q代表信息素增加的强度;α代表信息素的重要程度;β代表启发式因子的重要程度;P表示转移概率。
2)蚂蚁领域搜索的概率为:

(13)
其中:pi,j为蚂蚁从位置i转移到位置j的概率;τj为蚂蚁j的领域吸引强度;μi,j定义为MSE(Ti-Tj)。
3)τj表示为蚁群算法中信息更新的强度:

(14)

(15)
式中:Δτj代表在本次计算中第j只蚂蚁吸引强度的增加量;Lj为本次计算中MSE(T)的变化量。
4)判断算法是否收敛,如果没有收敛继续回到第二步骤继续搜索;如果收敛则全局搜索结束,得到最优阈值T。
设定蚂蚁数量50,迭代次数为100,α=1,β=6,ρ=0.1,Q=100,τ0=1,p=0.9,通过蚁群算法对阈值进行优化选取,6层小波分解系数对应的阈值为(0.492,1.331,0.352,0.056,0.061,0.058)。
2.3信号去噪流程
本文提出的去噪方法流程图如图2所示,首先对含噪信号进行小波变换,建立小波变换系数的最小均方差下阈值计算函数,在蚁群算法中优化选取最优阈值,对每层的小波系数做阈值处理,最后进行小波逆变换获得去噪后的信号。
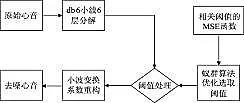
图2 心音去噪流程图Fig.2 The flow chart of heart sounds denoising
3实验结果与分析
3.1实验结果
实验数据来自赣南医学院第一附属医院的采集设备,采集的心音信号频率为11 025 Hz,量化值的位数为16 bit,采集的心音信号以WAV格式进行保存。
为验证本文提出的自适应阈值函数的有效性,采用正常心音信号为研究对象,选用db6小波并进行6层小波分解,分别选用硬阈值函数、软阈值函数、半软阈值函数、蚁群算法的优化阈值的半软函数等不同的小波去噪方法,去噪效果如图3所示。
图3(a)是采集到的含噪声的正常心音信号。图3(b)是原始心音信号经过db6小波硬阈值函数进行去噪处理,明显地观察出去噪后的效果图仍含有比较多的噪声。图3(c)是db6小波软阈值函数进行心音去噪的效果图,由图可知噪声得到很大的滤除,但是有些信号细节被平滑,S3、S4信号被平滑。图3(d)是原始心音信号使用db6小波半软阈值函数进行去噪处理后的图形,由图可知噪声得到很好的滤除,S3、S4分裂信号仍然无法识别。图3(e)是db6小波基于蚁群算法优化选取阈值的心音去噪效果图,由图可知噪声得到很好滤除,且保留了信号的细节特征,S3、S4分裂信号能够分辨清楚。

图3 阈值函数的去噪效果图Fig.3 The denoising effect of different threshold function
3.2阈值函数性能的分析
为了更为深入地了解不同的阈值函数对原始心音信号进行去噪后的效果,本文选取的评价标准为信噪比(SNR)和均方根误差(RMSE),计算结果如表1所示。

表1 去噪效果评价
由表1可知,软阈值函数的小波变换方法去噪后的信号信噪比最低,均方根误差最大也就是去噪效果最差;本文采用的基于蚁群算法优化选取阈值的小波变换去噪的信噪比和均方误差都得到了较大的改善。
4结论
本文客观地分析了传统软硬阈值函数去噪后存在的客观问题,即传统硬阈值函数处理原始心音后,重新构建的信号仍存在振荡;软阈值函数去噪后信号出现失真,一些小的细节信号也被平滑掉。通过建立基于最小均方误差的最优阈值选取函数,利用全局搜索性较好的蚁群算法搜索最小均方误差的各层最优阈值,通过与硬阈值函数滤波方法、软阈值函数滤波方法、半软阈值函数滤波方法进行实验结果对比,在噪声滤除的同时信号特征得到保留,S3、S4心音分裂信号清晰。证明了本文提出的基于蚁群算法选取阈值的心音去噪方法的有效性。
参考文献:
[1]梁庆真,郭兴明,袁志会. 局部投影和离散小波变换在心音信号去噪中的应用[J]. 振动与冲击,2014 (13):188-193.
[2]HASSANI K,BAJELANI K,NAVIDBAKHSH M,et al. Heart sound segmentation based on homomorphic filtering[J]. Perfusion, 2014,29(4):351-359.
[3]LI T,QIU T,TANG H. Optimum heart sound signal selection based on the cyclostationary property[J]. Computers in Biology and Medicine, 2013,43(6):607-612.
[4]吴玉春,杨亚萍,邓北川. 心音信号分段规则的探讨[J]. 北京生物医学工程,2014,33(5):524-526.
[5]PAULET A S,WAN E A,NELSON A T. Noise reduction for heart sounds using a modified minimum-mean squared error estimator with ECG gating[C]// 28th Annual International Conference of the IEEE. Chicago: University of Chicago Press, 2006:3385-3390.
[6]YUENYONG S,NISHIHARA A,KONGPRAWECHNON W,et al. A framework for automatic heart sound analysis without segmentation[J]. BioMed Eng OnLine, 2011,10(1):1-23.
[7]张维强,宋国乡. 基于一种新的阈值函数的小波域信号去噪[J]. 西安电子科技大学学报(自然科学版),2004,31(2):296-299,303.
[8]郭兴明,何彦青,卢德林,等. 平移不变小波在心音信号去噪中的应用[J]. 计算机工程与应用, 2014(24):209-212,235.
[9]陈远贵,罗保钦,曾庆宁. 基于一种新的小波阈值函数的心音信号去噪[J]. 计算机仿真,2010,27(11):319-323.
[10]黄敏,靳婷,钟声,等. 基于改进蚁群算法求解连续空间寻优问题[J]. 广西师范大学学报(自然科学版),2013,31(2):34-38.
(责任编辑李小玲)
A Heart Sound Denoising Method Based on Adaptive Threshold Wavelet Transform
ZHOU Keliang1, XING Sulin2, NIE Congnan2
(School of Electrical Engineering and Automation, Jiangxi University of Science and Technology, Ganzhou Jiangxi 341000,China;2.School of Mechanical and Electrical Engineering, Jiangxi University of Science and Technology,Ganzhou Jiangxi 341000,China)
Abstract:In the acquisition of heart sound signal, it is inevitable to introduce some noise so that the heart sound signal denoising must be done before the diagnosis of heart sound signals . Because the heart sound signal is nonlinear and non-stationary, wavelet transform denoising method is commonly used to remove noise of heart sound signal. However, traditional wavelet threshold function needs to customize the threshold, its denoising effect is not ideal, and may filter out a lot of useful details of the heart sound signal, which may hardly lead to a correct judgment. In order to solve the problem of the distortion of the heart sound signal denoising process in using traditional wavelet threshold function, on the basis of semi soft threshold function, a nonlinear wavelet transform denoising method based on ant colony optimization algorithm is proposed. Using the original heart sounds as the research object, by using the DB6 wavelet and 6 layer wavelet decomposition, this paper use different denoising methods such as hard threshold function, soft threshold function, semi soft threshold function and ant colony algorithm of the optimal threshold of semi soft function of wavelet denoising, compare the effects of these methods and then use ant colony algorithm global search to search for the optimal threshold in terms of minimum mean square error. Simulation results show that the ant colony optimization algorithm to select the threshold of the heart sound denoising can not only remove the noise, but also preserve the details of signal characteristics, and the method is more effective in noise reduction in comparison with the conventional soft and hard threshold functions. The method is more effective in noise reduction in comparison with the conventional soft and hard threshold function.
Keywords:heart sounds denoising ; wavelet transform; adaptive threshold; ant colony algorithm
中图分类号:TH911.7
文献标志码:A
文章编号:1001-6600(2016)01-0019-07
基金项目:国家自然科学基金资助项目(61363011)
收稿日期:2015-05-20
doi:10.16088/j.issn.1001-6600.2016.01.003
通信联系人:周克良(1963—),男,江西赣州人,江西理工大学教授。E-mail: nyzkl@sina.com

