可证明安全的基于位置的Prover-to-Prover密钥交换协议

张俊伟，陈治平，马建峰，杨　力

(西安电子科技大学计算机学院，陕西西安710071)



可证明安全的基于位置的Prover-to-Prover密钥交换协议

张俊伟，陈治平，马建峰，杨力

(西安电子科技大学计算机学院，陕西西安710071)

摘要：本文针对两个证明者之间可证明安全的基于位置密钥交换协议展开研究.首次将基于位置密钥交换分为P2V(Prover-to-Verifier)模式和P2P(Prover-to-Prover)模式，并给出P2P模式下基于位置密钥交换的安全定义.随后，在1维空间下设计了可证明安全的基于位置P2P密钥交换协议P2PKE1，并以此为基础构造了d(1≤d≤3)维空间下基于位置P2P密钥交换协议P2PKEd.同时，分别提出了具有密钥确认性质的基于位置P2P密钥交换协议P2PKEd-c和无密钥托管的基于位置P2P密钥交换协议P2PKEd-e.最后，从安全性和效率两方面对所设计的协议进行了讨论.

关键词：P2P;基于位置密钥交换; BRM模型;可证明安全

1　引言

随着无线设备的地理位置在无线系统的数据采集、安全通信、资源管理、异常处理/维护等多方面扮演越来越重要的角色，基于位置系统中与地理位置相关的安全问题也越发引人关注［1～3］.

Liu和Ning针对无线传感器网络提出了一个基于位置的密钥预分发方案［4］.Yang和Xiao应用基于网格多项式密钥建立方法来解决无线传感网络的安全问题［5］.Huang等针对无线传感网络提出了一种基于位置的密钥管理方案［6］，Younis等人则提出了一种基于位置的分布式密钥管理方案［7］.Zhang等人结合用户身份和地理位置得出基于位置密钥，并提出了一种基于位置的安全机制［8，9］.

作为基于位置的安全机制的核心，大多数的定位协议无法抵御多个敌手的共谋攻击，无法达到密码学意义的可证明安全［10］.

Chandran等人提出了基于位置密码学的概念［10］.基于BRM模型(Bounded Retrieval Model)，Chandran等人在BRM模型下实现了能够抵制共谋攻击的可证明安全的定位协议和基于位置的密钥交换协议.随后，一些量子计算环境下基于位置的密码协议也随之出现［11～13］.

然而，现有的基于位置密钥交换协议只能够实现证明者和验证者之间的密钥确立，即Prover-to-Verifier(P2V)模式.这种模式并不能直接应用于某些基于位置系统中.例如，参与方A(处于位置pa)希望与参与方B(处于位置pb)进行基于位置的密钥交换.

显然，在两个证明者之间的基于位置密钥交换，即Prover-to-Prover(P2P)模式，也是基于位置密钥交换中的一个重要任务.本文针对BRM模型下可证明安全的基于位置P2P密钥交换协议展开研究.具体如下:

(1)将基于位置密钥交换分为两个模式，即P2V模式和P2P模式.提出基于位置P2P密钥交换的安全定义.

(2)在BRM模型下，在1维空间下设计了一个基于位置的P2P密钥交换协议.

(3)在上述协议基础上，构建d维(1≤d≤3)空间下基于位置的P2P密钥交换协议.

(4)提出满足密钥确认(With Key Confirmation)的基于位置P2P密钥交换协议和无密钥托管(Without Key Escrow)的基于位置P2P密钥交换协议.

2　基于位置密钥交换的两种模式

2.1P2V模式

在P2V模式下，d维的基于位置密钥交换协议［10，11］包括:一个证明者，至少(d + 1)个验证者，以及多个共谋敌手.在P2V密钥交换协议完成之后，位于合法位置的证明者能够抵御多个共谋敌手的攻击，与验证者实现安全的密钥交换过程.已有的基于位置密钥交换协议都属于P2V模式，其中包括BRM模型下的密钥交换协议［10］，以及量子环境下的密钥协议［11～13］.

2.2P2P模式

与P2V模式不同，P2P模式实现(在验证者的辅助下)两个证明者之间基于位置的密钥交换，如图1所示.

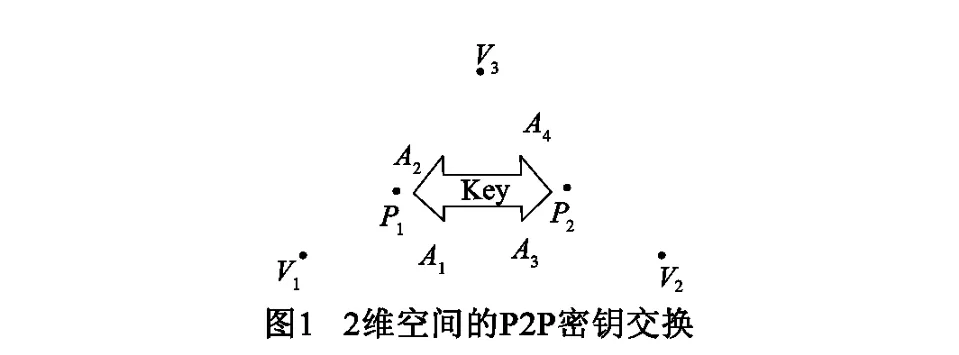
令π为d维空间基于位置P2P密钥交换协议.该协议由两个算法组成，即π=(Init，Key):位置初始化算法Init(P)和密钥交换算法Key(Ver，P1，p1，P2，p2).令验证者为Ver = { V0，V1，…，VD}，位置分别为pos0，pos1，…，posD且(D≥d).令PPT(probabilistic polynomial time)的共谋敌手为Adv = { A1，A2，…，AK}，位置分别为apos1，apos2，…，aposK.算法Init(P)可以初始化证明者P的位置，即Init(P)= p表示证明者P的位置为p.算法Key(Ver，P1，p1，P2，p2)能够抵御共谋敌手Adv = { A1，A2，…，AK}，在两个未被攻陷的证明者P1和P2之间建立一个共享密钥，即sk = Key(Ver，P1，p1，P2，p2)，其中P1位于p1，P2位于p2.

敌手的攻击模型如下:

(1)除了BRM模型中具有很高最小熵(high minentropy)的信息，敌手可以获取所有通过无线信道传输的信息.

(2)敌手可以在无线信道内发送任何伪造的信息.

(3)敌手可以处在除了p1和p2以外的任意位置.

定义1(基于位置P2P密钥交换)协议π=(Init，Key)是安全的基于位置P2P密钥交换协议(安全参数为k)当且仅当给定(Ver，P1，P2，p1= Init(P1)，p2= Init(P2))，对于任意的PPT共谋敌手Adv = { A1，A2，…，AK}仅能以可忽略概率ε(k)区分密钥sk = Key(Ver，P1，p1，P2，p2)和随机数U(|U| = |sk|).即

Pr［Adv(Ver，P1，p1，P2，p2)］- Pr［Adv(Ver，P1，p1，P2，p2)］＜ε(k).

利用P2V模式构造P2P密钥交换.证明者P1和P2可以利用基于位置P2V密钥交换分别与验证者(扮演可信第三方)协商密钥k1和k2.随后，P1和P2使用基于可信第三方的密钥分发协议，如Needham-Schroeder协议［14］，实现P1和P2之间的基于位置密钥交换.然而，该实现方法的缺点在于:验证者必须维护证明者当前位置与P2V模式下生成密钥之间的关联.对于验证者而言，维护这种密钥与位置之间关联容易带来安全隐患，且代价较大.

3　一维空间下基于位置P2P密钥交换协议

3.1BRM模型

BRM模型［10］假设所有的敌手只能检索到(具有很高最小熵的)信息的一部分.具体如下:

(1)验证者可以生成具有高最小熵值为(δ+β)n 的n比特串X.

(2)当X经过时，所有敌手都可以检索X的任何部分，但是所有敌手检索的总信息量不能超过一个上限βn.

3.2BSM伪随机生成器

定义2(BSM伪随机生成器)令存储率为β，最小熵率为α.PRG: { 0，1}n×{ 0，1}r→{ 0，1}t是ε-secure的BSM伪随机生成器(BSM pseudorandom generators，BSM PRG)，当且仅当对于{ 0，1}n上任意的αnsource的X，对于任意A: { 0，1}n→{ 0，1}βn，随机变量(PRG(X，K)，A(X)，K)对(W，A(X)，K)是ε-close的，其中K为{ 0，1}r上的随机数，W是ψ-source的.根据εsecure的BSM PRG的定义［10］可得，对于任意算法F，给定A(X)和K，算法F(A(X)，K)能正确计算PRG(X，K)的最大概率为ε+2-ψ，其中2-ψ是可忽略的.

在安全参数为κ的情况下，如果r≥(2/δ)κlb(n)，那么ε+ 2-ψ是可忽略的.在BRM模型下，只要选择合适的r，敌手能够正确计算PRG(X，K)的概率是可忽略的.

3.3前提假设

假设1(保密信道)在基于位置密码学中，假设所有验证者之间都存在一条保密信道，即验证者之间可以安全的进行信息传输.

假设2(广播认证)假设每一个验证者已存在认证的广播信道，即任何敌手都不能更改或者伪造验证者发送的信息.

已有的研究存在很多可用于基于位置密码学的高效广播认证协议，如μTESLA［15］、一次签名协议［16］等.

需要说明的是，文献［10］以及本文所提出的基于位置密码协议都假设除了传播时延外，其他时延均为零，即所有参与方都能够即时收发和处理数据而没有延迟.

3.4协议P2PKE1

在1维空间中，使用两个验证者V0和V1(令Ver = { V0，V1} )，二者传输的数据以无线电波的速度进行传播.本文假设证明者P1和P2的位置p1和p2都处于V0和V1之间.P2PKE1协议的具体描述如下:

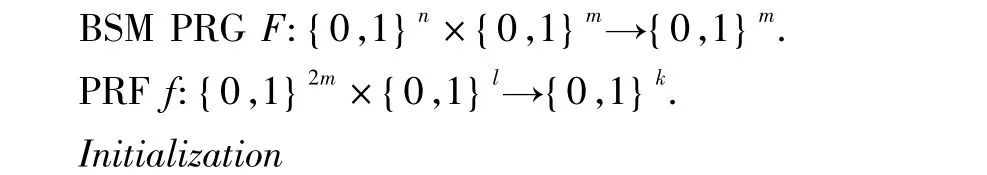
证明者P1和P2分别运行Init(P1)和Init(P2):

(1 )令P1位置为p1= Init(P1)，P2位置为p2= Init(P2).

(2)令s =(sid，p1，p2)，其中sid是会话标识.令t(Vi，p)为信息从验证者Vi到达位置p所传播的时间.令T1和T2分别为验证者V0发送的信息到达p1和p2的时刻，其中T1- T2= t(V0，p1)- t(V0，p2).

Key Exchange

证明者P1和P2运行Key(Ver，P1，p1，P2，p2):

(1)V0生成最小熵为(δ+β)n的X0和随机数r，V1生成最小熵为(δ+β)n的X1和X2，V0和V1安全共享X0，X1，X2和r.

(2)V0计算y1= F(X1，r)，z1= F(X0，y1)，y2= F(X2，r)，z2= F(X0，y2)，令z = z1⊕z2.V0在时刻T1-t(V0，p1)通过认证的广播信道发送(X0，r，z，s).

(3)V1分别在时刻T1- t(V1，p1)和T2- t(V1，p2)通过认证的广播信道发送(X1，s)和(X2，s).

(4)在T1时刻收到(X0，r，z，s)和(X1，s)，P1计算y1= F(X1，r)，z1=F(X0，y1)，z2=z⊕z1，sk =f(z1，z2，1).

(5)当在T2时刻收到(X0，r，z，s)和(X2，s)，P2计算y2=F(X2，r)，z2=F(X0，y2)，z1=z⊕z2，sk =f(z1，z2，1).

3.5安全性分析

定理1如果F是ε-secure BSM PRG，f是PRF，Xi(0≤i≤2)具有最小熵(δ+β)n，βn是检索上限，那么协议P2PKE1在共谋攻击下是安全的基于位置P2P密钥交换协议.

证明不失一般性，令所有的共谋敌手{ A1，A2，…，AK}被敌手G控制.令S0，S1，S2分别为所有敌手对X0，X1，X2所检索的总信息，且| S0|≤βn，| S1|≤βn，|S2|≤βn.

假设P2PKE1协议是不安全的，即敌手G能以不可忽略的概率εG区分由Key(Ver，P1，p1，P2，p2)生成的密钥sk和随机比特串U.根据P2PKE1协议，会话密钥sk应等于f(z1，z2，1).如果敌手G成功攻击P2PKE1协议，则存在以下两种可能的事件:

事件1没有z1和z2的情况下，敌手G能够区分密钥sk和随机比特串U.

用ε1表示事件1发生的概率，如果ε1不可忽略，则可构造敌手Af，以概率εf(ε1=εf)来攻击f.很明显，这与PRF的定义相矛盾，即事件1发生的概率是忽略的.

事件2敌手G可以计算正确的z1和z2.

令ε2表示事件2发生的概率，如果敌手G可以计算出(z1，z2)，则存在以下五个可能的情况:

情况1给定(S1，r)，敌手G计算y1= F(X1，r).

令A1为V1和p1之间的敌手.由于G能够计算y1，当X0经过时A1能够计算z1= F(X0，y1)和z2= z⊕z1，进一步可以计算出密钥sk = f(z1，z2，1).由此可见，如果敌手G计算出y1，则敌手A1就能够区分密钥sk和随机数.

假设给定(S1，r)，敌手G以不可忽略的概率计算出y1= F(X1，r)，则可以构造一个敌手AF1，给定(S*，r*)，AF1能够区分y*= F(X*，r*)和随机比特串U，其中F是ε-secure的BSM PRG(ε是可忽略的).

用ε21表示敌手G能够计算y1= F(X1，r)的概率，则敌手AF1能够区分y*= F(X*，r*)和U的概率是:

如果ε21是不可忽略的，则εF1也是不可忽略的，这与ε-secure的BSM PRG定义相矛盾.

情况2给定(S1，r)后，敌手G可以计算y2= F(X2，r).

令A2为V1和p2之间的敌手.如果敌手G能够以概率ε22计算出y2，则敌手A2也能够计算z1和z2.

同样，可以构造敌手AF2以εF2的概率来攻破BSM PRG的伪随机性，即εF2=ε22-1/2m≈ε22.

如果ε22的概率不可忽略，则εF2也不可忽略.

情况3给定(S0，y1)，敌手G可以计算z1= F(X0，y1).

令A3为V0和p1之间的敌手.A3可以计算y1= F(X1，r).假设敌手G以不可忽略的概率ε23计算z1= F(X0，y1)，则能构造敌手AF3以不可忽略的概率εF3成功攻击BSM PRG，即εF3=ε23- 1/2m≈ε23.这与BSM PRG的定义相矛盾.

情况4给定(S0，y2)，敌手G可以计算z2= F(X0，y2).

令A4为V0和p2之间的敌手.如果敌手G能以不可忽略的概率ε24计算z2= F(X0，y2)，则能构造敌手AF4以不可忽略的概率εF4成功攻击F，其中εF4=ε24-1/2m≈ε24.

情况5敌手G能成功猜测随机数r.

令A5为V1和p1之间的敌手.如果敌手G可以成功猜测r，则当X1经过时敌手A5可以计算y1= F(X1，r).然而，r是随机数，则敌手G能够猜出r的概率ε25是可忽略的.因此，敌手A5在情况5下计算出y1的概率也是可忽略的.

综上所述，敌手G能够攻击P2PKE1协议的概率为:

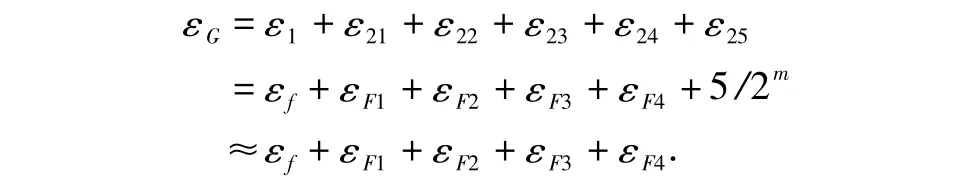
因此，如果f是PRF，F是ε-secure BSM PRG，那么εf，εF1，εF2，εF3，εF4以及εG都是可以忽略的.定理1得证.

4　d维空间下基于位置P2P密钥交换协议

在d维空间中，协议P2PKEd需要至少(d + 1)个验证者才能实现P2P密钥交换.在BRM模型下，P2PKEd协议的具体描述如下:

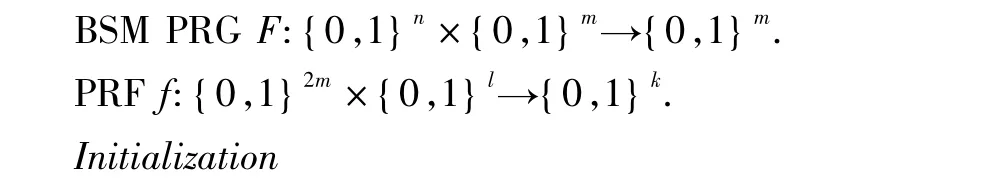
与P2PKE1协议的Initialization相同.

Key Exchange

(1)验证者V0生成具有高最小熵(δ+β)n的比特串X0以及m比特的随机数r，验证者Vi生成具有高最小熵(δ+β)n(1≤i≤d)的比特串X(i，1)和X(i，2).所有验证者通过保密信道共享X0，{ X(i，j)}(1≤i≤d，1≤j≤2)以及r.

(2)V0计算z1= F(X0，r(0，1))和z2= F(X0，r(0，2))，其中r(i -1，j)= F(X(i，j)，r(i，j))，r(d，j)= r(1≤i≤d，1≤j≤2)，z = z1⊕z2.V0在T1- t(V0，p1)时刻通过认证的广播信道发送(X0，r，z，s).

(3)Vi分别在T1- t(Vi，p1)和T2- t(Vi，p2)时刻通过认证的广播信道发送(X(i，1)，s)和(X(i，2)，s)(1≤i≤d).

(4)当在T1时刻收到(X0，r，z，s)和{ X(1，1)，…，X(d，1)}时，证明者P1计算z1= F(X0，r(0，1))，其中r(i -1，1)= F(X(i，1)，r(i，1))，r(d，1)= r(1≤i≤d).令z2= z⊕z1，并计算sk = f(z1，z2，1).

(5)当在T2时刻收到(X0，r，z，s)和{ X(1，2)，…，X(d，2)}时，证明者P2计算z2= F(X0，r(0，2))，其中r(i -1，2)= F(X(i，2)，r(i，2))，r(d，2)= r(1≤i≤d).令z1= z⊕z2，并计算sk = f(z1，z2，1).

定理2如果F是ε- secure的BSM PRG，f是PRF，X0和{ X(i，j)}具有最小熵(δ+β)n(1≤i≤d，1≤j≤2)且βn为检索上界，则P2PKEd协议在共谋攻击下是安全的.

定理2的证明与定理1的证明相似，此处不再赘述.另外，Chandran已经讨论了2维或者3维空间中可用于基于位置密钥交换的有效区域问题.无论是P2V模式还是P2P模式，除了靠近验证者的很小区域之外，大部分区域都可以用于基于位置密钥交换［10］.

5　协议的扩展

5.1密钥确认

基于P2PKEd协议，本节提出具有密钥确认性质的P2P基于位置密钥交换协议P2PKEd-c.与协议P2PKEd相比，协议P2PKEd-c添加了Rekey阶段，如下所示:

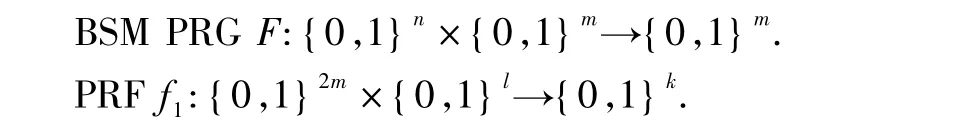
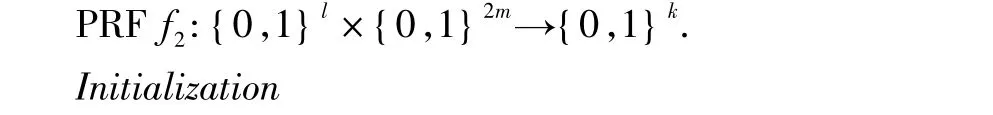
与P2PKE1协议的Initialization相同.

Key Exchange

(1)，(2)，(3)步骤与P2PKEd协议中(1)，(2)，(3)相同.

(4)在T1时刻收到(X0，r，z，s)和{ X(1，1)，…，X(d，1)}后，P1计算z1= F(X0，r(0，1))，其中r(i -1，1)= F(X(i，1)，r(i，1))，r(d，1)= r(1≤i≤d)，z2= z⊕z1.令ak = f1(z1，z2，0)，ek = f1(z1，z2，1).

(5)在T2时刻收到(X0，r，z，s)和{ X(1，2)，…，X(d，2)}后，P2计算z2= F(X0，r(0，2))，其中r(i -1，2)= F(X(i，2)，r(i，2))，r(d，2)= r(1≤i≤d)，令z1= z⊕z2.令ak = f1(z1，z2，0)，ek = f1(z1，z2，1).

Rekey

(1)P1选择随机数r1，发送(P1，s，r1)给P2.

(2)收到(P1，s，r1)，P2选择随机数r2，计算sk = f2(ek，(r1，r2))，c2= f2(ak，(P2，s，r2，r1))，发送(P2，s，r2，c2)给P1.

(3)收到(P2，s，r2，c2)，P1首先验证c2的正确性.如果验证成功，计算sk = f2(ek，(r1，r2))和c1= f2(ak，(P1，s，r1，r2))，发送(P1，s，c1)给P2，将sk作为共享密钥.

(4)收到(P1，s，c1)，P2验证c1的正确性.如果验证成功，P2输出的sk作为共享密钥.

显而易见，P2PKEd-c协议具有密钥确认的性质.下面分析P2PKEd-c协议的安全性.

定理3如果F是ε-secure BSM PRG，f1和f2都是PRFs，X0和{ X(i，j)}具有最小熵(δ+β)n(1≤i≤d，1≤j ≤2)且βn为检索上界，那么协议P2PKEd-c在共谋攻击下是安全的.

证明证明分为以下两个步骤:

(1)ak和ek的机密性

由定理1可得，共谋敌手只能在可忽略概率下得到sk，同理可得在P2PKEd-c协议中，共谋敌手也只能在可忽略概率下得到ak和ek.

(2)Rekey阶段的安全性

引理1 Rekey阶段可以为证明者P1和P2实现安全的密钥交换.

基于ak和ek的机密性，引理1的证明与文献［17］对REKEY协议的分析类似，这里不再赘述.

综上，P2PKEd-c协议满足定义1.定理3得证.

5.2无密钥托管

在之前的协议中，假设所有验证者都是可信的.由 P2PKEd协议(以及P2PKEd-c协议)可知，所有验证者都能得到P1和P2之间的共享密钥，即存在密钥托管问题.

假设3(DDH假设)令G为循环群，秩为素数q，本原根为g，α和β是Zq上的随机数.任意的PPT敌手A只能以可忽略的概率来区分{ gα，gβ，gαβ}和{ gα，gβ，R}，其中R是随机数且|R| = |gαβ|.

基于DDH(Decision Diffie-Hellman)假设，通过添加DH Exchange阶段可以实现无密钥托管的基于位置P2P密钥交换协议P2PKEd-e.P2PKEd-e协议如下:

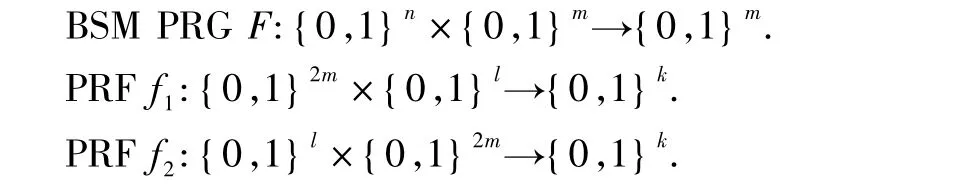
循环群G:秩为素数q，本原根为g.

Initialization＆Key Exchange

与P2PKEd-c协议相似.唯一的不同之处在于证明者P1和P2只计算ak，不计算ek.

DH Exchange

(1)P1从Zq中随机选择α，并发送(P1，s，gα)给P2.

(2)收到(P1，s，gα)后，P2从Zq中随机选择β，计算sk =(gα)β，c2= f2(ak，(P2，s，gβ，gα))，发送(P2，s，gβ，c2)给P1.

(3)收到(P2，s，gβ，c2)后，P1首先验证c2的正确性.如果验证成功，计算sk =(gβ)α以及c1= f2(ak，(P1，s，gα，gβ)).然后P1发送(P1，s，c1)给P2并输出sk作为共享密钥.

(4)收到(P1，s，c1)后，P2验证c1的正确性.如果验证成功，P2输出sk作为共享密钥.

显然，协议P2PKEd-e具有密钥确认的性质.此外，该协议还满足无密钥托管的需求.

定理4如果DDH假设成立，则在P2PKEd-e协议中，所有半可信的验证者都只能以可忽略的概率区分共享密钥sk和随机数，即协议具有无密钥托管的性质.

证明该定理的证明可以直接规约为DDH假设.如果存在一个半可信的验证者V以不可忽略的概率区分sk和随机数，那么就能构造一个PPT敌手A来解决DDH问题.显然，这与DDH假设相矛盾.定理4得证.

定理5如果DDH假设成立，F是ε-secure BSM PRG，f1和f2都是PRFs，X0和{ X(i，j)}具有最小熵(δ+ β)n(1≤i≤d，1≤j≤2)且βn为检索上界，P2PKEd-e协议是安全的.

证明与定理3类似，定理5的证明也分为两个步骤:

(1)ak的机密性

由定理1的可得，共谋攻击者无法得到ak.

(2)DH Exchange阶段的安全性

引理2 DH Exchange阶段可以为证明者P1和P2实现安全的密钥交换.

本质上，DH Exchange阶段是基于MAC的DH密钥交换协议.根据基于MAC认证器和DDH假设，DH Exchange阶段可以实现安全的密钥交换［17］.

综上可得，P2PKEd-e协议是安全的基于位置P2P密钥交换协议，定理5得证.

6　性能比较

以3维空间的协议为例，对协议P2PKE3，P2PKE3-c 和P2PKE3-e进行比较，结果如表1所示.

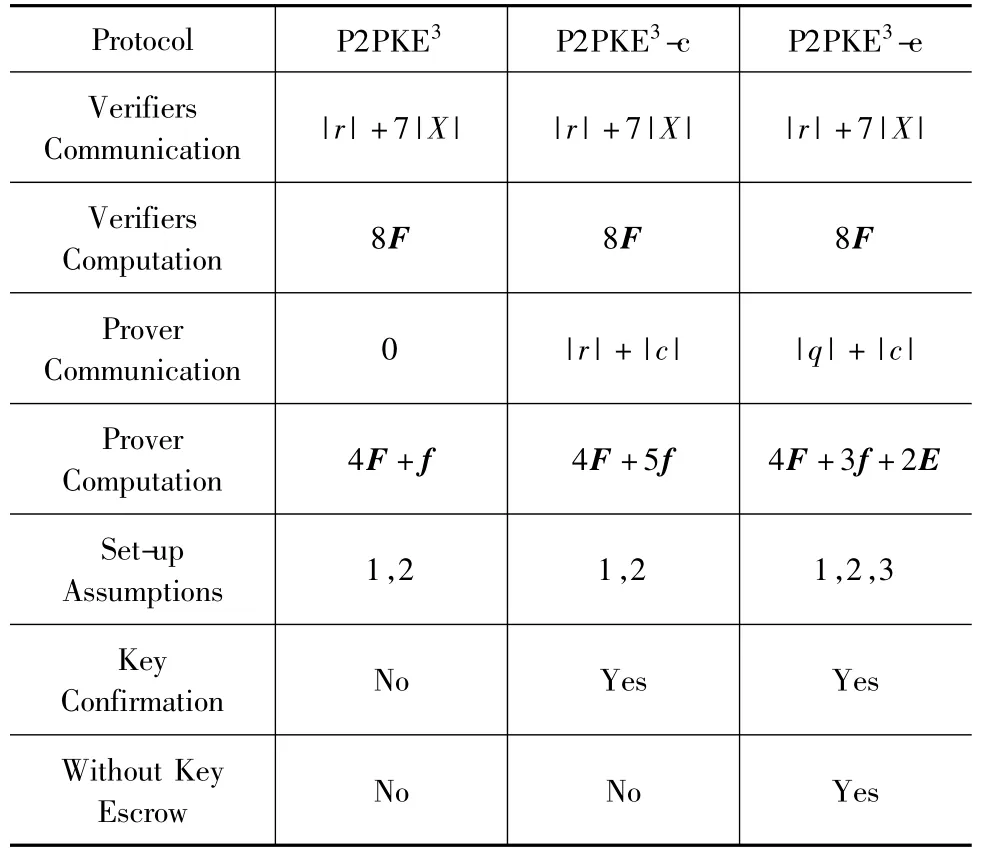
表1　比较结果

安全性显然，在BRM模型以及假设1、假设2下，协议P2PKE3，P2PKE3-c和P2PKE3-e都是安全的.此外，P2PKE3-c协议具有密钥确认的性质，而P2PKE3-e协议在DDH假设下具有密钥确认和无密钥托管的性质.

效率从验证者角度，通信开销和计算代价在三个协议中都是一样的.换言之，P2PKE3-c协议和P2PKE3-e协议不会对验证者有额外的代价.

P2PKE3协议中证明者没有通信开销，因此P2PKE3协议更适用于能量受限的应用环境.

P2PKE3-c协议在Rekey阶段给证明者增加了额外的通信开销和计算代价.

在P2PKE3-e协议中，证明者引入了计算代价较高的模指运算.可以使用椭圆曲线或者其他更高效的密钥交换来减少计算开销.

7　结论

本文首次给出了基于位置P2P密钥交换的概念和安全定义.设计了1维空间下基于位置P2P密钥交换协议P2PKE1，并以此为基础提出了在d维空间中的基于位置P2P密钥交换协议P2PKEd.结合P2P模式下的密钥交换的安全需求，进一步提出了具有密钥确认性质的P2PKEd-c协议以及无密钥托管性质的P2PKEd-e协议.

参考文献

［1］B Rao，L Minakakis.Evolution of mobile location-based services［J］.Communications of the ACM，2003，46(12): 61 -65.

［2］肖竹，王勇超，田斌，于全，易克初.超宽带定位研究与应用:回顾和展望［J］.电子学报，2011，39(1): 133 -141.Xiao Zhu，Wang Yongchao，Tian Bin，Yu Quan，Yi Kechu.UWB positioning research and application: review and outlook［J］.Acta Electronica Sinica，2011，39(1): 133 - 141.(in Chinese)

［3］林云松，孙卓振，彭良福.基于Bancroft算法的多点定位TOA-LS估计［J］.电子学报，2012，40(3): 621 -624.Lin Yunsong，Sun Zhuozhen，Peng Liangfu.Multipoint positioning TOA-the LS estimate of the algorithm based on the Bancroft［J］.Acta Electronica Sinica，2012，40(3): 621 -624.(in Chinese)

［4］D Liu，P Ning.Location-based pairwise key establishments for static sensor networks［A］.Proceedings of the 1st ACM Workshop on Security of ad hoc and Sensor Networks［C］.ACM，2003.72 -81.

［5］C Yang，J Xiao.Location-based pairwise key establishment and data authentication for wireless sensor networks［A］.Information Assurance Workshop［C］.IEEE，2006.247 -252.

［6］D Huang，M Mehta，D Medhi，L Harn.Location-aware key management scheme for wireless sensor networks［A］.2nd ACM Workshop on Security of ad hoc and Sensor Networks［C］.ACM，2004.29 -39.

［7］M Younis，K Ghumman，M Eltoweissy.Location-aware combinatorial key management scheme for clustered sensor networks［J］.IEEE Transactions on Parallel and Distributed Systems，2006，17(8): 865 -882.

［8］Y Zhang，W Liu，W Lou，Y Fang.Securing sensor networks with location-based keys［A］.IEEE Wireless Communications and Networking Conference［C］.IEEE，2005.1909 -1914.

［9］Yanchao Zhang，Wei Liu，Wenjing Lou，Yuguang Fang.Location-based compromise-tolerant security mechanismsfor wireless sensor networks［J］.IEEE J Select Areas Commun，2006，24(2): 247 -260.

［10］N Chandran，V Goyal，R Moriarty，R Ostrovsky.Positionbased Cryptography［A］.Advances in Cryptology-CRYPTO 2009［C］.Berlin: Springer-Verlag，2009.391 -407.

［11］H Buhrman，N Chandran，S Fehr，R Gelles，V Goyal，R Ostrovsky，C Schaffner.Position-based quantum cryptography: impossibility and constructions［A］.Advances in Cryptology-CRYPTO 2011［C］.Berlin: Springer-Verlag，2011.429 -446.

［12］H K Lau，H K Lo.Insecurity of position-based quantumcryptography protocols against entanglement attacks［J］.Physical Review A，2011，83(1): 012322.

［13］M Tomamichel，S Fehr，J Kaniewski，S Wehner.One-sided device-independent QKD and position-based cryptography from monogamy games［A］.Advances in Cryptology-EUROCRYPT 2013［C］.Berlin: Springer-Verlag，2013.609 -625.

［14］Junwei Zhang，Jianfeng Ma，Chao Yang.Protocol derivation system for the Needham-Schroeder family［J］.Wiley Online Library，2012.DOI:10.1002/sec.565.

［15］A Perrig，R Szewczyk，J D Tygar，V Wen，D E Culler.SPINS: security protocols for sensor networks［A］.ACM Conference on Mobile Computing and Networks［C］.ACM，2001.189 -199.

［16］J Zhang，J Ma，S Moon.Universally composable one-time signature and broadcast authentication［J］.Sci China Inf Sci，2010，53(3): 567 -580.

［17］R Canetti，H Krawczyk.Analysis of key-exchange protocols and their use for building secure channels［A］.Advances in Cryptology-EUROCRYPT 2001［C］.Berlin: Springer-Verlag，2001.2045:453 -474.

张俊伟男，1982年2月生于陕西西安.博士，西安电子科技大学副教授，主要研究方向为网络与信息安全、密码学等.

E-mail: jwzhang@ xidian.edu.cn

陈治平男，1990年2月生于安徽阜阳.西安电子科技大学硕士研究生，主要研究方向为无线网络安全.

Provably Secure Position-BasedProver-to-Prover Key Exchange Protocols

ZHANG Jun-wei，CHEN Zhi-ping，MA Jian-feng，YANG Li
(School of Computer Science and Technology，Xidian University，Xi’an，Shaanxi 710071，China)

Abstract:This paper investigates provably secure position-based key exchange protocols between two provers.To begin with，this paper presents the notions of the prover-to-verifier mode and the prover-to-prover mode，which is the first to distinguish between the two modes for position-based key exchange.At the same time，this paper formalizes the definition of secure prover-to-prover position-based key exchange.Then，a provably secure prover-to-prover position-based key exchange protocol P2PKE1in 1-dimension is proposed in this paper.Based on the above protocol，a generic prover-to-prover positionbased key exchange protocol P2PKEdin d-dimensions is constructed(1≤d≤3).In addition，this paper extends the proposed protocol and proposes protocol P2PKEd-c with key confirmation and protocol P2PKEd-e without key escrow in d-dimensions.Finally，we discuss the proposed protocols in 3-dimensions from both security and performance perspectives.

Key words:prover-to-prover; position-based key exchange; bounded retrieval model; provable security

作者简介

基金项目:长江学者和创新团队发展计划(No.IRT1078);国家科技重大专项(No.2011ZX03005-002);国家自然科学基金(No.U1135002，No.61100230，No.61100233，No.61202389，No.61202390，No.61372075，No.61472310);中央高校基本科研业务费(No.JY10000903001，No.K5051303003)

收稿日期:2014-07-01;修回日期: 2014-11-15;责任编辑:李勇锋

DOI:电子学报URL：http: / /www.ejournal.org.cn10.3969/j.issn.0372-2112.2016.01.003

中图分类号：TN911.7

文献标识码：A

文章编号：0372-2112(2016)01-0014-07