一种改进阈值法陀螺信号消噪的研究

韩 东

（西安航空职业技术学院招生就业处，西安 710089）

光纤陀螺（FOG）是一种全固态惯性器件，已经在捷联式惯性导航系统中得到广泛的应用，它具有寿命长、耐冲击、动态范围宽等优点[1]。但同时也具有一些缺点，例如：在受到外界环境影响，温度变化、以及冲击和振动等引起的噪声混叠，就会严重影响陀螺输出的精度。对这些噪声的干扰要进行补偿设计，要在得到他们准确的统计特性基础上，建立一个环境变量的多维模型，而通过辨识噪声参数、在线实时拟合等方法来得到这个模型在实现上存在一定的困难。而对光纤陀螺输出进行补偿时不用其漂移模型，直接滤波，通过对信号的消噪到达抑制干扰噪声是可行的[2]。

利用小波分析的时频局部化特性、多分辨分析的优点，可以根据信号和噪声在小波域具有不同的特征将有效的信号和噪声分离开来。因此，在光纤陀螺信号的消噪方面采用小波分析方法被认为是一种非常有效的方法[3]。在小波分析的基础上提出来了小波包理论，它能够为信号提供一种更紧密细致的分析方法，从而获得更细致的时频局部化信息。

在光纤陀螺输出信号中主要存在广义高斯白噪声和1/f γ分形噪声[4]。本文结合陀螺噪声的特点，分类估计噪声强度，使用小波包消噪方法对陀螺输出进行处理时，根据分解尺度自适应地确定阈值，并提出一种连续的阈值函数，规避了传统的硬阈值函数和软阈值函数存在的缺陷。与传统阈值消噪相比，新算法能有效去除噪声，更好地保留真实信号，在静态和动态情况下均具有较好效果。

1 小波包分解与重构原理

小波变换实质上是把信号分解为不同尺度和频率的小波子空间。小波变换只对信号的低频部分做进一步分解，而对高频部分不予考虑，小波包针对信号频带进行多层次的划分，对高频段进一步进行分解，能够根据被分析信号的特征，自适应地选择相应频带[5-6]。

定义子空间是函数φn(t)的闭包空间，令φn(t)满足下面的双尺度方程。

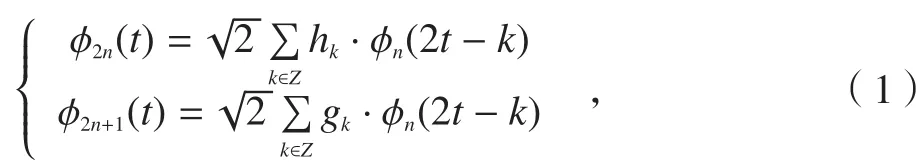
式中，即两系数具有正交关系。设可表示为：

式中是在中投影的系数。

小波包分解算法：

小波包分解的实质是通过h、g这一对低、高通组合正交镜像滤波器进行组合采样，把信号逐层分解到不同频段上。小波包分解的频段宽度Δf与分解层数j及采样频率fS满足关系式：

由上式可得，选择适当的分解层数可得到频段宽度及各频段起止频率，就可以分离陀螺信号中的特征信号和干扰噪声。

小波包的重构算法：

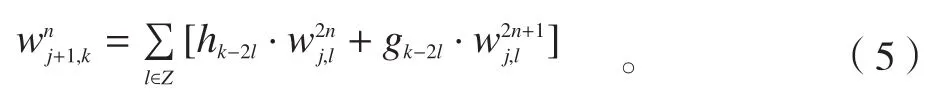
2 光纤陀螺噪声的估计

光纤陀螺误差按照噪声项的来源可分为5种：偏置不稳定性噪声、角度随机游走噪声、速率斜坡噪声速率、随机游走噪声和量化噪声。它们是功率谱密度和频率的γ成反比的1/f γ分形噪声。光纤陀螺的输出可表示为：

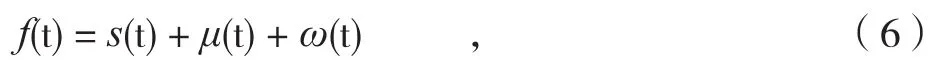
式中，μ(t)表示分形噪声，ω(t)表示高斯白噪声。假设μ(t)与ω(t)相互独立不相关，s(t)表示陀螺输出的有效信号。对光纤陀螺静态输出数据进行去常值漂移和线性趋势项的预处理，有效信号非常弱，已经淹没在噪声中，近似有s(t)≈0。则式（6）可改写为：

f(t)即为零漂信号。

2.1 高斯白噪声方差估计

对于式（7）所示的陀螺信号计算其自相关函数。

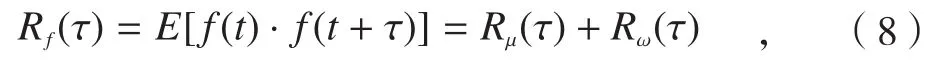
式中为高斯白噪声方差。

由式（8）知，陀螺信号的自相关函数在τ=0处为白噪声方差与分形噪声自相关函数之和。因此，通过陀螺信号自相关函数在非零点的值拟合Rf(τ)-τ曲线，估计出零点值，则可由信号源自相关函数零点值与拟合估计的零点值相减得到的估计值。然而完全不相关的白噪声是不存在的，实测的陀螺信号自相关函数与单纯的1/f γ分形噪声自相关函数在非零处上是不可能完全重合的，因此，引入总延迟时间T来提高拟合精度，更加准确的白噪声强度进行估计。具体确定T的方法参见文献[7]，文中不再复述。

2.2 分形噪声方差估计

1/f γ分形噪声在时域是非平稳的，对其进行小波变换后，用表示尺度为j时，k时刻的小波系数。若变换所用的小波基具有R阶消失矩，对于0＜γ＜2R，分形噪声在尺度j时的小波系数是零均值，方差为的弱相关平稳随机序列表示分形噪声时域的方差。在相同尺度下，序列的相关性随R的增加而呈指数下降，当R较大时，序列几乎不相关。采用具有高阶消失矩的小波函数对式（7）所示信号进行小波变换，可得各尺度下小波系数的方差关系式：

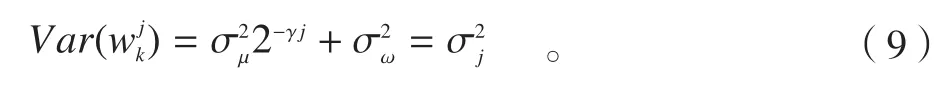
由于白噪声的噪声水平不随小波分解尺度的变化而改变，因此式（9）中的即为2.1节中估计出的白噪声方差值。对式（9）移项后两边取对数得：

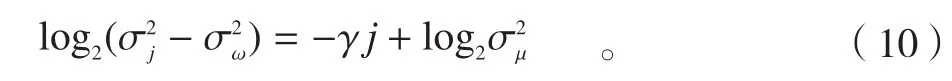
式中可由直接计算各尺度小波系数方差得到。将分解尺度j作为自变量作为因变量，通过最小二乘拟合的方法得到分形噪声方差和参数γ[8]。

3 小波包阈值消噪

在小波包标架中，其信号消噪的算法思想与一般小波消噪基本一致，都是通过对小波域系数进行阈值处理以达到去除噪声的目的，最大限度保留有效信号小波系数，实现降噪。小波包分析是对上一层的低频部分和高频部分进行细分，因此具有更为精确的局部分析能力。因此对信号进行第J层小波包分解时有2J组分解系数，而引入小波包变换是为了让能量集中，也就是在小波系数中寻找有序性[9]，因此，把所有部分都进行分解对解决问题是没有帮助的。这就需要有一定的衡量标准，一般采用最小熵原则。熵是用来度量信息规律性的概念，熵越小信息的规律性就越强，据此准则可以得到一个信号分解的树状结构，称为小波树。那么寻求最优小波树就是力图使分解有最大的规律性，把信号内在规律挑出来。

3.1 阈值选取和改进

阈值的确定以及函数的选取是小波阈值消噪算法的两个关键的问题，它们将直接影响到消噪的效果。要根据信号中所含噪声特征选择合适的阈值。若阈值太小，去噪后的信号仍然存有噪声；阈值过大，则可能将信号的主要特征也一并滤除掉，引起偏差。目前，常用的阈值准则为：

式中，N为给定细节子带的小波系数长度，σ为信号噪声的标准差，它可由第一层分解下由小波系数的绝对值中值M来估计。

上述阈值是系数间相互独立的，且噪声为白噪声的假设推导出的，在不同的尺度上阈值变化规律相同。然而，光纤陀螺信号中除了含有白噪声外还有分形噪声，信号为非平稳序列，由此通过M估计噪声水平，不能很好地反映噪声变化的规律，进而计算阈值就会存在偏差。而且依该准则计算的阈值受信号长度影响，系数长度N过大时，λ趋向于将所有小波系数置零，易产生“过扼杀”系数的情况，增大重构误差。

针对上述问题，并考虑到阈值随分解尺度增大而逐渐减小的特点，本文采用Normal Shrink准则计算阈值。

对不同的子带，所选取的阈值大小跟分解的尺度、子带系数长度密切相关。由于陀螺信号中主要包括白噪声和分形噪声，所以σ2按下式估计：

式中，白噪声方差和分形噪声方差分别由2.1节和2.2节的方法得到。

3.2 一种新的连续阈值函数

目前，软阈值方法和硬阈值方法在实际中得到广泛应用。

硬阈值函数为：

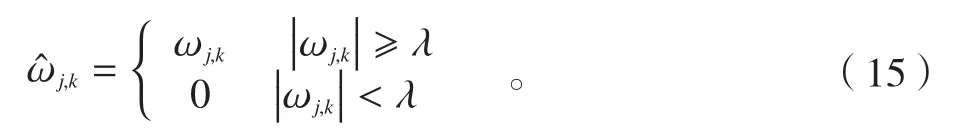
软阈值函数为：

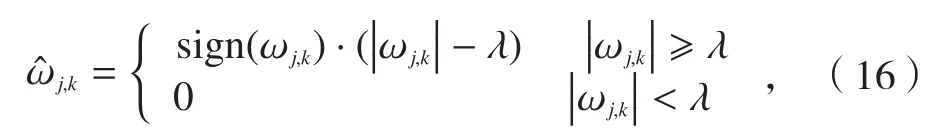
式中，sign表示取符号运算。硬阈值法去噪效果较好，但该函数在±λ处不连续，易引起重构信号的振荡，在不连续点处消噪后会出现伪吉布斯现象；软阈值方法计算出来的虽然整体连续性好，降噪效果相对平滑，但在间总存在恒定的偏差，使得重构信号对真实信号的逼近程度得到严重影响。并且它们的导数不连续，在实际应用中需要对一阶导数甚至高阶导数进行处理时，这两种阈值函数存在一定局限性。为了这些缺点，国内外的科学家研究了很多阈值函数改进方法，但其中大都表达式复杂，并且分段取值。本文提出一种连续的阈值函数，它具有连续的高阶导数，在时可以较快逼近硬阈值函数。

新的阈值函数选择以2为底的指数函数做收缩系数，便于在计算机上实现。该阈值函数主要针对含有少量真实信息的小波系数处理上，将这些系数做收缩处理，最大程度的保留真实信号，消减绝对值接近或低于阈值的小波系数，使它们远远小于其他系数。式（17）中α、β为正整数，随着α的增大由趋于零收缩变为趋于ωj,k的转折段越来越远离原点，当α=4时该转折段在阈值附近；β越大，新方法计算的越逼近于硬阈值，不过随着β增大计算量也相应增大。在阈值附近，新阈值函数具有软阈值函数的作用，它可使得阈值消噪以较为平滑的方式实现，使在阈值附近的小波系数收缩后更加接近原信号的小波系数，从而能有效抑制由于直接截断可能引起的虚假振荡。

4 仿真试验

首先，选用光纤陀螺静态漂移数据对消噪方法进行检验，将某干涉型光纤陀螺固定在水平转台上，其输入敏感轴指向正东方向，对准误差控制在角秒范围，转台保持静止，采样频率20Hz。分别采用通用阈值的小波包消噪法和改进阈值函数的小波包消噪法处理陀螺输出。用db4小波基分解至5层，以Shannon熵作为熵标准确定最优小波树，通用阈值消噪时采用硬阈值函数，改进阈值消噪时参数α、β仍取4和5。

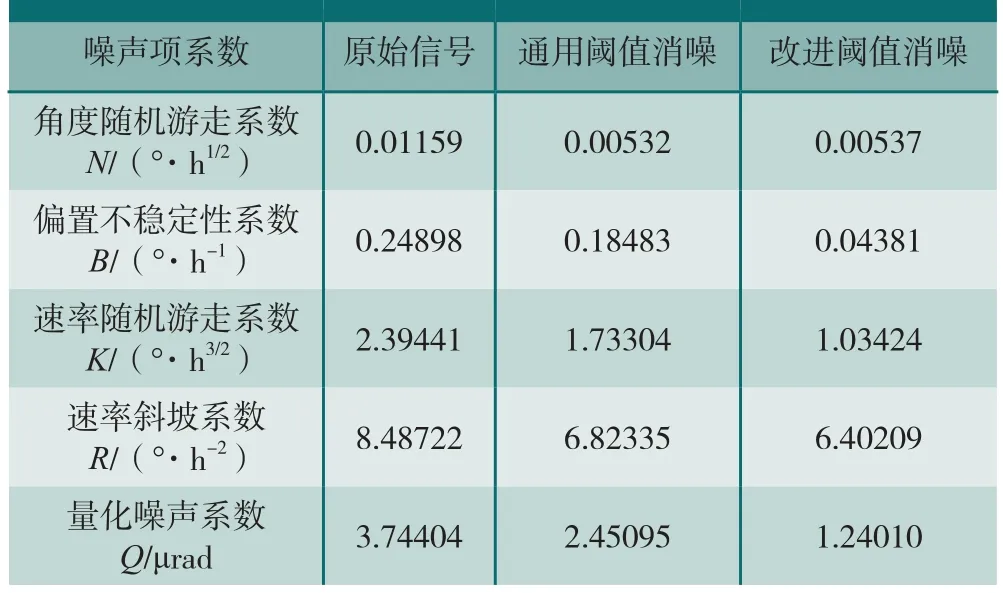
表1 光纤陀螺静态输出小波包消噪前后各噪声系数

陀螺原始输出数据如图1（a）所示，其中含有大量非平稳随机噪声。通过小波包通用阈值法消噪后,信号波形变为图1（b），噪声得到较好抑制，信号标准差由消噪前的0.39979°/h降至0.10744°/h，但由于阈值函数截断消噪后信号存在振荡，波形不够平滑。图1（c）是采用改进阈值消噪后的信号波形，标准差为0.10046°/h，消噪效果优于通用阈值法，而且有效避免了振荡[10]。

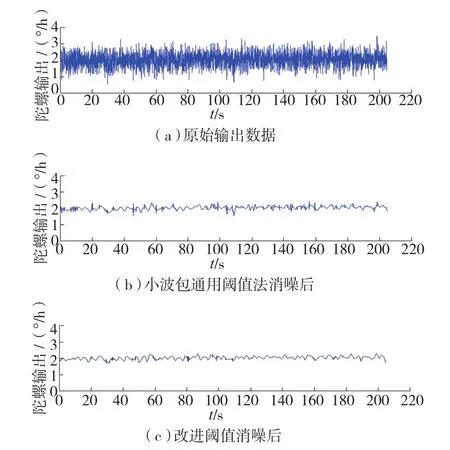
图1 光纤陀螺原始输出信号及小波包消噪后信号Fig.1 Original output signal of fiber optic gyro and wavelet packet de-noising signal

对消噪前后的陀螺静态漂移信号进行Allan方差分析，以确定存在于信号中的各项噪声水平。

从消噪前后拟合得到的各项随机误差系数可以看出，在经过了小波包消噪后各项误差都得到一定程度的减小，并且文中所提方法对噪声的抑制效果要更好些。

为验证对光纤陀螺动态输出信号的滤波效果，利用Matlab中的bumps信号作为陀螺输出的有效信号，通过数字信号处理的方法模拟各噪声项：用广义白噪声模拟角度随机游走噪声；用高斯白噪声的一次积分模拟速率随机游走噪声；用均值为零，方差为LSB2/2的高斯白噪声模拟量化噪声，LSB表示角度量化的最低有效位；用随机速率斜坡函数模拟速率斜坡噪声；用正交小波变换的方法模拟偏置不稳定性噪声[11]；用一阶Markov过程来模拟指数相关噪声。按不同的信噪比将信号与噪声叠加在一起，模拟含噪的光纤陀螺动态输出信号，进行小波包消噪处理。

滤波前模拟含噪信号的信噪比（SNR）为25dB，信号波形如图2（a）所示。图2（b）是经通用阈值法消噪后的信号，信噪比提高到34.95dB，而改进阈值法消噪后结果为图2（c），信噪比为35.63dB。

对于模拟的光纤陀螺动态输出设定不同的信噪比，经过两种阈值方法消噪后，信噪比改善情况（消噪前后信噪比之差）如图3所示。从图中可看出，在各种信噪比输入下，本文提出的改进阈值消噪法对信噪比的改善效果均要优于通用阈值法。

图2 模拟光纤陀螺动态输出信号的小波包消噪Fig.2 Wavelet packet de-noising for simulating the dynamic output signal of fiber optic gyro

图3 信噪比改善曲线Fig.3 Signal to noise ratio improvement curve

5 结论

采用小波包消噪法处理光纤陀螺输出信号，可以在各尺度上更加细致地对噪声进行抑制。文中对以往小波包阈值消噪法的阈值和阈值函数进行改进，提出一种连续的阈值函数用于小波系数处理。通过对陀螺静态输出的消噪验证和动态信号的仿真处理，证明改进的阈值方法可以更好地保存原信号中的尖峰和突变特征，同时有效抑制噪声。这是因为在新算法中，各层小波系数的阈值是根据所在层噪声的幅度自适应调节的，并且估计噪声方差时针对光纤陀螺噪声项特点进行辨识计算，比单纯选用第一层小波分解系数中值做估计要精确，且新的连续阈值函数使小波系数阈值处理以较为平滑的方式实现，在阈值附近具有相似于软阈值函数的作用，在阈值之上时又具有硬阈值函数的作用，使滤波后小波系数取值更加接近原信号小波系数取值。改进的阈值方法在计算量上比通用阈值法有所增加，适用于对消噪处理实时性要求不高，但消噪精度要求较高的场合。

[1]周泓.光纤陀螺的应用与发展[J].国防技术基础,2010(3):41-42.

ZHOU Hong. Application and development of fiber optic gyro[J].Technology Foundation of National Defence, 2010(3):41-42.

[2]ZHU Yunzhao, WANG Shunting, MIAO Lingjuan. Open loop FOG signal testing and wavelet eliminating noise [J]. Transactions of Nanjing University of Aeronautics & Astronautics, 2005, 22(2):103-106.

[3]付强文,张英敏.光纤陀螺信号处理的实用方法 [J].传感技术学报, 2005,18(1): 101-104.

FU Qiangwen, ZHANG Yingmin. A Practical method of fiber optic gyro signal processing[J]. Journal of Sensing Technology, 2005, 18(1):101-104.

[4]SKALOUD J, BRUTON A M, SCHWARZ K P. Detection and filtering of short-term(1/f γ) noise in inertial sensors [J]. Navigation, 1999,46(2):97-107.

[5]陈婧,宋凝芳,李敏.小波分析在光纤陀螺分形噪声模拟中的应用[J].电光与控制, 2010, 17(5):50-53.

CHEN Jing, SONG Ningfang, LI Ming. Application of wavelet analysis in simulation of fractal noise of fiber optic gyroscope[J]. Electronics Optics& Control, 2010, 17(5):50-53.

[6]钱华明,马吉臣,李仲玉.基于小波包阈值处理的光纤陀螺信号降噪[J].中国惯性技术学报, 2007, 15(5):602-605.

QIAN Huaming, MA Jichen, LI Zhongyu. Fiber optic gyro signal denoising based on wavelet packet threshold processing [J]. Journal of Chinese Inertial Technology, 2007, 15(5):602-605.

[7]何凯,王树勋,戴逸松.估计 类分形信号信噪比的新方法[J].吉林大学学报, 2004, 34(1):36-38.

HE Kai, WANG Shuxun, DAI Yisong. New SNR estimation method to1/f fractal signal [J]. Journal of Jilin University of Technology(Natural Science Edition), 2004, 34(1):36-38.

[8]武华伍,任章.光纤陀螺中分形噪声的参数估计和去除.北京航空航天大学学报, 2008, 34(6):630-633.

WU Huawu, REN Zhang. Parameter estimation and elimination to fractal noise of fiber optic gyro[J]. Journal of Beijing University of Aeronautics and Astronautics, 2008, 34(6):630-633.

[9]徐东星.基于小波变换的数字信号去噪方法[D].武汉：湖北大学, 2008.

XU Dongxing. Digital signal denoising method based on wavelet transform [D]. Wuhan:Hubei University, 2008.

[10]ALLAN D.W. Statistics of atomic frequency standards [J].Proceedings of the IEEE, 1996, 54(2):221-230.

[11]葛升民,边志强,韩良军,等.光纤陀螺随机误差特性仿真与辨识[J].测试技术学报, 2008, 22(4):328-332.

GE Shengmin, BIAN Zhiqiang, HAN Liangjun, et al. Research on simulation and identification of random error properties for FOG[J]. Journal of Test and Measurement Technology, 2008, 22(4):328-332.