Analysis of X(5568)as Scalar Tetraquark State in Diquark-Antidiquark Model with QCD Sum Rules∗
Zhi-Gang Wang(王志刚)
Department of Physics,North China Electric Power University,Baoding 071003,China
1 Introduction
Recently,the D0 collaboration observed a narrow structure,X(5568),in the decay chainsX(5568)→→J/ψϕ,J/ψ→µ+µ−,ϕ→K+K−with significance of 5.1σbased on 10.4 fb−1ofcollision datacollected at the Fermilab Tevatron collider.[1]The mass and natural width of the new state areMX=MeV and ΓX=21.9±respectively.Thesystems consist of two quarks and two antiquarks of four different flavors.The D0 collaboration fi tted thesystems with the Breit–Wigner parameters in relative S-wave,the favored quantum numbers areJP=0+.However,the quantum numbersJP=1+cannot be excluded according to de-where the low-energy photon is not detected.
In this article,we assume theX(5568)to be the scalar diquark-antidiquark type tetra quark state.There are fi ve types diquarks,scalar diquarks,pseudoscalar diquarks,vector diquarks,axialvector diquarks and tensor diquarks according to the structures in Dirac spinor space.The favored con figurations are the scalar diquarks and axialvector diquarks from the QCD sum rules.[2−3]The heavy scalar and axialvector diquarks have almost degenerate masses,[2]while the masses of the light axialvector diquarks lie(150–200)MeV above the corresponding light scalar diquarks.[3]We take the scalar light diquark and heavy diquark as the basic constituents,[4]construct the scalar-diquark-scalar-antidiquark type current,which is expected to couple potentially to the lowest state,to study the mass and pole residue of theX(5568)with the QCD sum rules.[5−6]In the charm sector,theDs(2307)has been studied as the scalar-diquark-scalar-antidiquark type tetra quark state based on the QCD sum rules.[7]
The article is arranged as follows:We derive the QCD sum rules for the mass and pole residue of theX(5568)in Sec.2;In Sec.3,we present the numerical results and discussions;and Sec.4 is reserved for our conclusion.
2 QCD Sum Rules for theX(5568)as Scalar Tetraquark State
In the following,we write down the two-point correlation function Π(p)in the QCD sum rules,

where thei,j,k,m,nare color indexes,theCis the charge conjugation matrix.
We insert a complete set of intermediate hadronic states with the same quantum numbers as the current operatorJ(x)into the correlation function Π(p)to obtain the hadronic representation.[5−6]After isolating the ground state contribution of the scalar tetra quark state,we get the following result,

where the pole residueλXis defined by
In the following,we carry out the operator product expansion.We contract theu,d,sandcquark fields in the correlation function Π(p)with Wick theorem,and obtain the result:
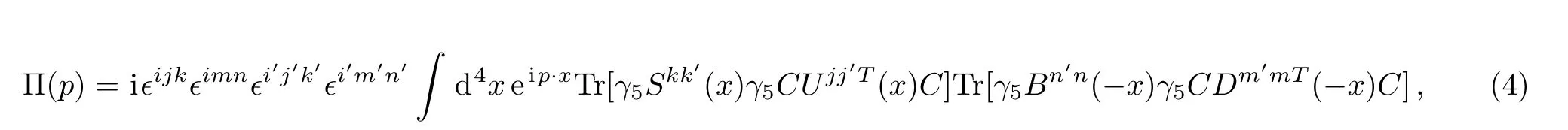
where theUij(x),Dij(x),Sij(x)andBij(x)are the fullu,d,sandbquark propagators respectively(theUij(x),Dij(x),Sij(x)can be written asSij(x)for simplicity,whereq=u,d,s),
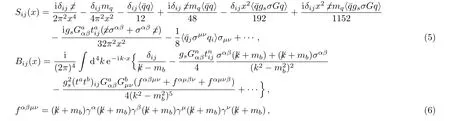
andtn=λn/2,theλnis the Gell–Mann matrix,[6]then compute the integrals both in the coordinate space and momentum space to obtain the correlation function Π(p)at the quark level,therefore the QCD spectral density through dispersion relationρ(s)=ImΠ(s)/π.The explicit expression is neglected for simplicity.In Eq.(5),we retain the termscome from the Fierz re-arrangement of theto absorb the gluons emitted from other quark lines to extract the mixed condensatesseveral new terms appear and play an important role in determining the Borel window.
In this article,we carry out the operator product expansion up to the vacuum condensates of dimension-10,and assume vacuum saturation for the higher dimension vacuum condensates.The condensatesare the vacuum expectations of the operators of the orderO(αs).We take the truncationsn≤10 andk≤1 in a consistent way,the operators of the ordersO()withk>1 are neglected.The condensateshave no contributions.
Once the spectral density at the quark level is obtained,we can take the quark-hadron duality below the continuum thresholds0and perform Borel transform with respect to the variableP2=−p2to obtain the QCD sum rule:

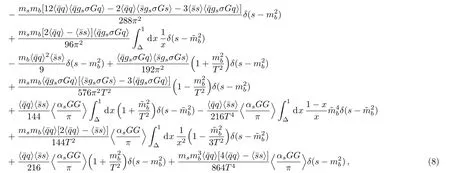
∆when theappears.
We differentiate Eq.(7)with respect to 1/T2,then eliminate the pole residueλX,and obtain the QCD sum rule for the mass of theX(5568),
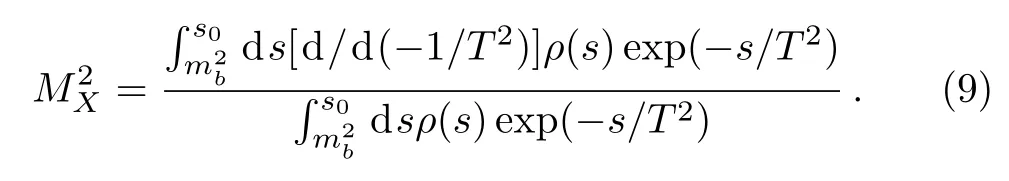
3 Numerical Results and Discussions
The input parameters are shown explicitly in Table 1.The quark condensates,mixed quark condensates andmasses evolve with the renormalization group equation,we take into account the energy-scale dependence according to the following equations,

Λ=213 MeV,296 MeV,and 339 MeV for the flavorsnf=5,4,and 3,respectively.[9]Furthermore,we set theuanddquark masses to be zero.
In Refs.[10–11],we study the acceptable energy scales of the QCD spectral densities for the hidden charm(bottom)tetra quark states in the QCD sum rules in details for the first time,and suggest a formulato determine the energy scales,
where theX,Y,Zare the four-quark systems,and theQare the effective heavy quark masses.The energy scale formula has been successfully extended to study the charmed baryon states and hidden-charm pentaquark states.[12]Recently,we re-checked the numerical calculations and found that there exists a small error involving the mixed condensates.[11]The Borel windows are modified slightly and the numerical results are also improved slightly after the small error is corrected,the conclusions survive,the optimal value of the effective mass isb=5.17 GeV instead of 5.13 GeV for the hidden-bottom tetra quark states.In this article,we use the energy scale formulato determine the optimal energy scale and obtain the valueµ=2.1 GeV.
In this article,the QCD spectral densityρ(s)∝snwithn≤4,the integraldsconverges slowly,it is difficult to obtain the pole contribution larger than 50%.In calculations,we use the QCD spectral densityρ(s)θ(s−s0)to approximate the continuum contribution with the valueGeV,where we take it for granted that the energy gap between the ground state and the first radial excited state is about(0.4–0.6)GeV,just like the conventional mesons and the hidden-charm tetra quark states,theZ(4430)is assigned to be the first radial excitation of theZc(3900).[13−14]Now we search for the optimal Borel parameterT2according to the two criteria(pole dominance and convergence of the operator product expansion)of the QCD sum rules.The optimal Borel parameterT2=(4.5–4.9)GeV2,the pole contribu-tion is about(15–29)%.At the operator product expansion side,the contributions of the vacuum condensatesDiof dimensionihave the relations,D3,D6,|D8|,D9≫D0,D4,|D5|,D7,D10,D0+D3≈40%,D4+D5≈−1%,D6≈66%,D7+D8+D9≈−10%,D10≈5%.The dominant contributions come from the termsD0+D3+D6,the operator product expansion is convergent,but the pole contribution is smaller than 30%,we cut down the continuum contamination by the threshold parameters0.The radial excited states or high resonances have to be included in,if one wants to obtain QCD sum rules with the pole contributions larger than 50%.[15]
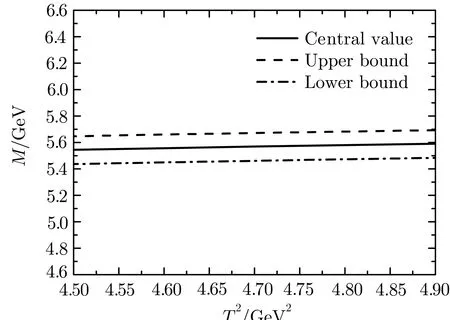
Fig.1 The mass MXwith wariation of the Borel parameter T2.
We take into account all uncertainties of the input parameters,and obtain the values of the mass and pole residue of theX(5568)as the scalar diquark-antidiquark type tetra quark state,
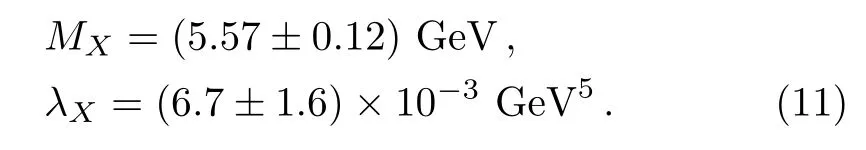
In Fig.1,we plot the predicted mass with variation of the Borel parameter.From the figure,we can see that the platform is rather fl at,and we expect to make reasonable prediction.The predicted massMX=(5.57±0.12)GeV is consistent with the experimental dataMX=(5567.8±MeV from the D0 collaboration.[1]
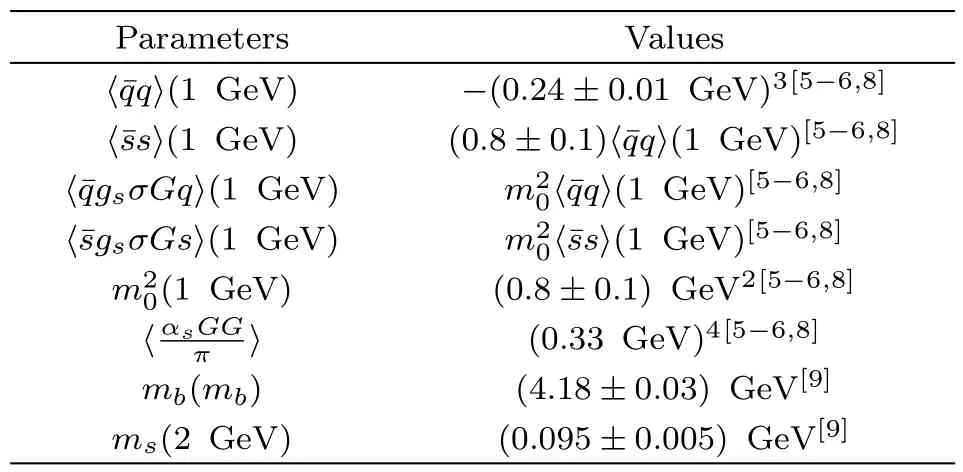
Table 1 The input parameters in the QCD sum rules,the values in the bracket denote the energy scalesµ=1 GeV,2 GeV and mb,respectively.
In Ref.[16],Zanetti,Nielsen and Khemchandani choose the same interpolating current as the present work,while in Ref.[17],Agaev,Azizi and Sundu choose the axialvector-diquark-axialvector-antidiquark type scalar current.If we apply the identityϵijkϵimn=δjmδkn−δjnδkmin the color space to the currentJ(x),we can obtain the current used in Ref.[18]in studying theX(5568)as a scalar tetra quark state with the QCD sum rules.In Ref.[18],Chenet al.also study theX(5568)as the axialvector tetra quark state and reproduce the experimental value of the massMX(5568).The quantum numbersJP=1+cannot be excluded according to decaysX(5568)→→,where the low-energy photon is not detected.The present article and Refs.[16–18]appeared in the net http://arxiv.org/on the same day,and the calculations were done independently.In Refs.[17–18],the parameters in Table 1 are taken directly to evaluate the QCD spectral densities,while in the present work we evolve the values to a special energy scaleµ=2.1 GeV determined by the energy scale formula.The input parameters chosen in Ref.[16]are different from the values used in the present work and in Refs.[17–18].The experimental value of the massMX(5568)can be well reproduced in the present work and in Refs.[16–18].
In the following,we perform Fierz re-arrangement to the currentJboth in the color and Dirac-spinor spaces to obtain the result,
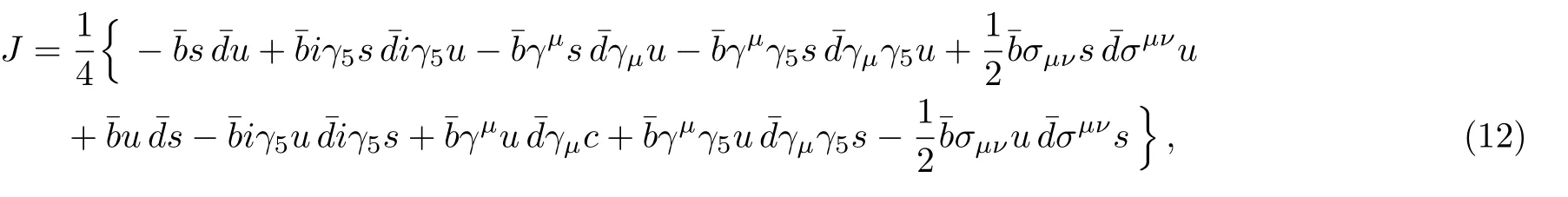
wherethejandkare color indexes.The componentsandcouple potentially to the meson pairwhile the componentscouple potentially to the meson pairThe strong decays
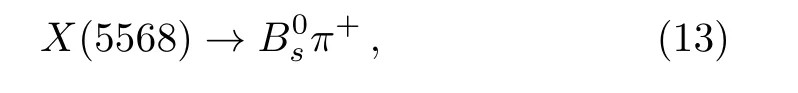
are Okubo–Zweig–Iizuka super-allowed,while the decays
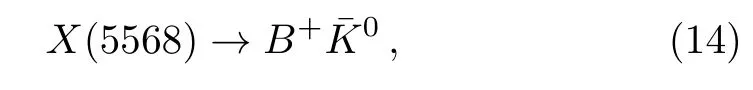
are kinematically forbidden,which is consistent with the observation of the D0 collaboration.[1]The present work favors assigning theX(5568)to be the scalar diquarkantidiquark type tetra quark state.
In Ref.[19],Burns and Swanson argue that it is unusual to assign theX(5568)to be the threshold effect,the−Bsπcusp withJP=1−,theBsπ−cusp withJP=0+,the Gamow–Gurney–Condon type resonance induced by theBsπ−interaction,the compact tetra quark state based on phenomenological analysis.In Ref.[20],Guo,Meissner and Zou provide additional arguments using the chiral symmetry and heavy quark symmetry. According to the constituent quark model,the constituent diquark model,the chiral symmetry and heavy quark symmetry,the lowest mass of thetetra quark state withJP=0+is much larger than theMX(5568),[19−21]for more references on this subject,one can consult Refs.[19–20].In the present work and in Refs.[16–18],theX(5568)is assigned to be the compact tetra quark state,the experimental value of the massMX(5568)can be well reproduced based on the QCD sum rules.In Ref.[22],the partial decay width of the strong decayX(5568)→is studied with the three-point QCD sum rules.If we saturate the width of theX(5568)with the strong decayX(5568)→B0sπ+,the experimental value ΓX=21.9±6.4+5.0−2.5MeV can be reproduced approximately.More theoretical works and more experimental data are still needed to approve existence or non-existence of theX(5568).
4 Conclusion
In this article,we take theX(5568)to be the scalar diquark-antidiquark type tetra quark state,construct the scalar-diquark-scalar-antidiquark type current,carry out the operator product expansion up to the vacuum condensates of dimension-10,and study the mass and pole residue of theX(5568)in details with the QCD sum rules.In calculations,we use the formulato determine the energy scale of the QCD spectral density.The present prediction favors assigning theX(5568)to be the scalar tetra quark state.The pole residue can be taken as basic input parameter to study relevant processes of theX(5568)with the three-point QCD sum rules.
[1]V.M.Abazov,et al.,Phys.Rev.Lett.117(2016)022003.
[2]Z.G.Wang,Eur.Phys.J.C 71(2011)1524;R.T.Kleiv,T.G.Steele,and A.Zhang,Phys.Rev.D 87(2013)125018.
[3]Z.G.Wang,Commun.Theor.Phys.59(2013)451.
[4]L.Maiani,A.Polosa,F.Piccinini,and V.Riquer,Phys.Rev.Lett.93(2004)212002.
[5]M.A.Shifman,A.I.Vainshtein,and V.I.Zakharov,Nucl.Phys.B 147(1979)385,448.
[6]L.J.Reinders,H.Rubinstein,and S.Yazaki,Phys.Rept.127(1985)1.
[7]M.E.Bracco,A.Lozea,R.D.Matheus,F.S.Navarra,and M.Nielsen,Phys.Lett.B 624(2005)217;H.Kim and Y.Oh,Phys.Rev.D 72(2005)074012;Z.G.Wang and S.L.Wan,Nucl.Phys.A 778(2006)22.
[8]P.Colangelo and A.Khodjamirian,arXiv:hep-ph/0010175.
[9]K.A.Olive,et al.,Chin.Phys.C 38(2014)090001.
[10]Z.G.Wang,Eur.Phys.J.C 74(2014)2874.
[11]Z.G.Wang and T.Huang,Nucl.Phys.A 930(2014)63.
[12]Z.G.Wang,Eur.Phys.J.C 75(2015)359;Z.G.Wang,Eur.Phys.J.C 76(2016)70.
[13]L.Maiani,F.Piccinini,A.D.Polosa,and V.Riquer,Phys.Rev.D 89(2014)114010;M.Nielsen and F.S.Navarra,Mod.Phys.Lett.A 29(2014)1430005.
[14]Z.G.Wang,Commun.Theor.Phys.63(2015)325.
[15]Z.G.Wang,Nucl.Phys.A 791(2007)106.
[16]C.M.Zanetti,M.Nielsen,and K.P.Khemchandani,Phys.Rev.D 93(2016)096011.
[17]S.S.Agaev,K.Azizi,and H.Sundu,Phys.Rev.D 93(2016)074024.
[18]W.Chen,H.X.Chen,X.Liu,T.G.Steele,and S.L.Zhu,Phys.Rev.Lett.117(2016)022002.
[19]T.J.Burns and E.S.Swanson,arXiv:1603.04366[hep-ph].
[20]F.K.Guo,U.G.Meissner,and B.S.Zou,Commun.Theor.Phys.65(2016)593.
[21]W.Wang and R.L.Zhu,arXiv:1602.08806[hep-ph].
[22]Z.G.Wang,Eur.Phys.J.C 76(2016)279;J.M.Dias,K.P.Khemchandani,A.Martinez Torres,M.Nielsen,and C.M.Zanetti,Phys.Lett.B 758(2016)235;S.S.Agaev,K.Azizi,and H.Sundu,Phys.Rev.D 93(2016)114007.
 Communications in Theoretical Physics2016年9期
Communications in Theoretical Physics2016年9期
- Communications in Theoretical Physics的其它文章
- Abundance of Asymmetric Dark Matter in Brane World Cosmology∗
- Critical Behaviors and Finite-Size Scaling of Principal Fluctuation Modes in Complex Systems∗
- Self-Focusing/Defocusing of Chirped Gaussian Laser Beam in Collisional Plasma with Linear Absorption∗
- A Three Higgs Doublet Model for Fermion Masses∗
- Stationary Probability and First-Passage Time of Biased Random Walk∗
- Lie Symmetry Analysis,Conservation Laws and Exact Power Series Solutions for Time-Fractional Fordy–Gibbons Equation∗
