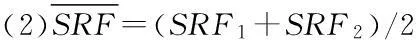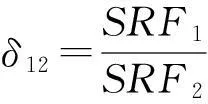有限元双折减系数法的边坡稳定性应用

邹希煊，张俊萍

(江西理工大学建筑与测绘工程学院，江西 赣州　341000)



有限元双折减系数法的边坡稳定性应用

邹希煊，张俊萍

(江西理工大学建筑与测绘工程学院，江西 赣州341000)

摘要：通过设计基于有限元分析的双折减系数法的边坡稳定分析程序，对一边坡进行边坡稳定分析，得出随内摩擦角折减系数逐渐增大，而粘聚力折减系数逐渐减小，边坡失稳时塑性破坏区于坡顶呈现逐渐收缩态势。

关键词：双折减系数法；边坡稳定分析；塑性破坏

1双折减系数法

基本理论一般的，边坡稳定性分析中的极限平衡法和强度折减法的抗剪强度指标c、φ是应用相同的折减系数进行折减的。随着对折减系数初期的基数进行固定合理的增量运算，边坡会逐渐达到极限平衡状态，该状态唯一且被定义为边坡的安全系数，记为Fs。

唐芬、郑颖人等提出的双折减系数法则把c、φ的折减系数认定为不一致，采用不同的值进行强度折减，见式(1)

(1)

式中：SRF1为内摩擦角φ的折减系数；SRF2为粘聚力c的折减系数；c1、φ1为折减后土体的粘聚力和内摩擦角。

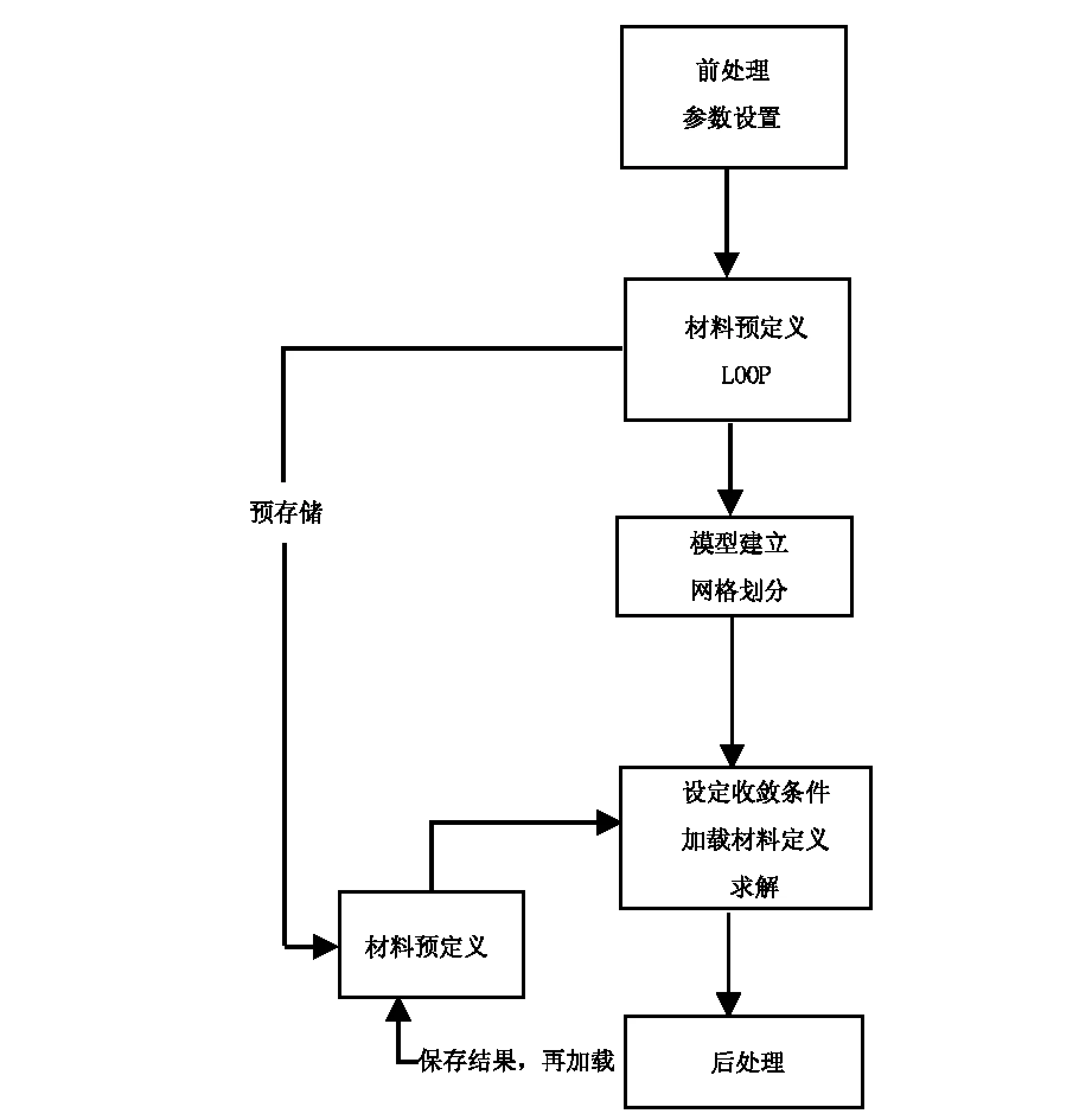
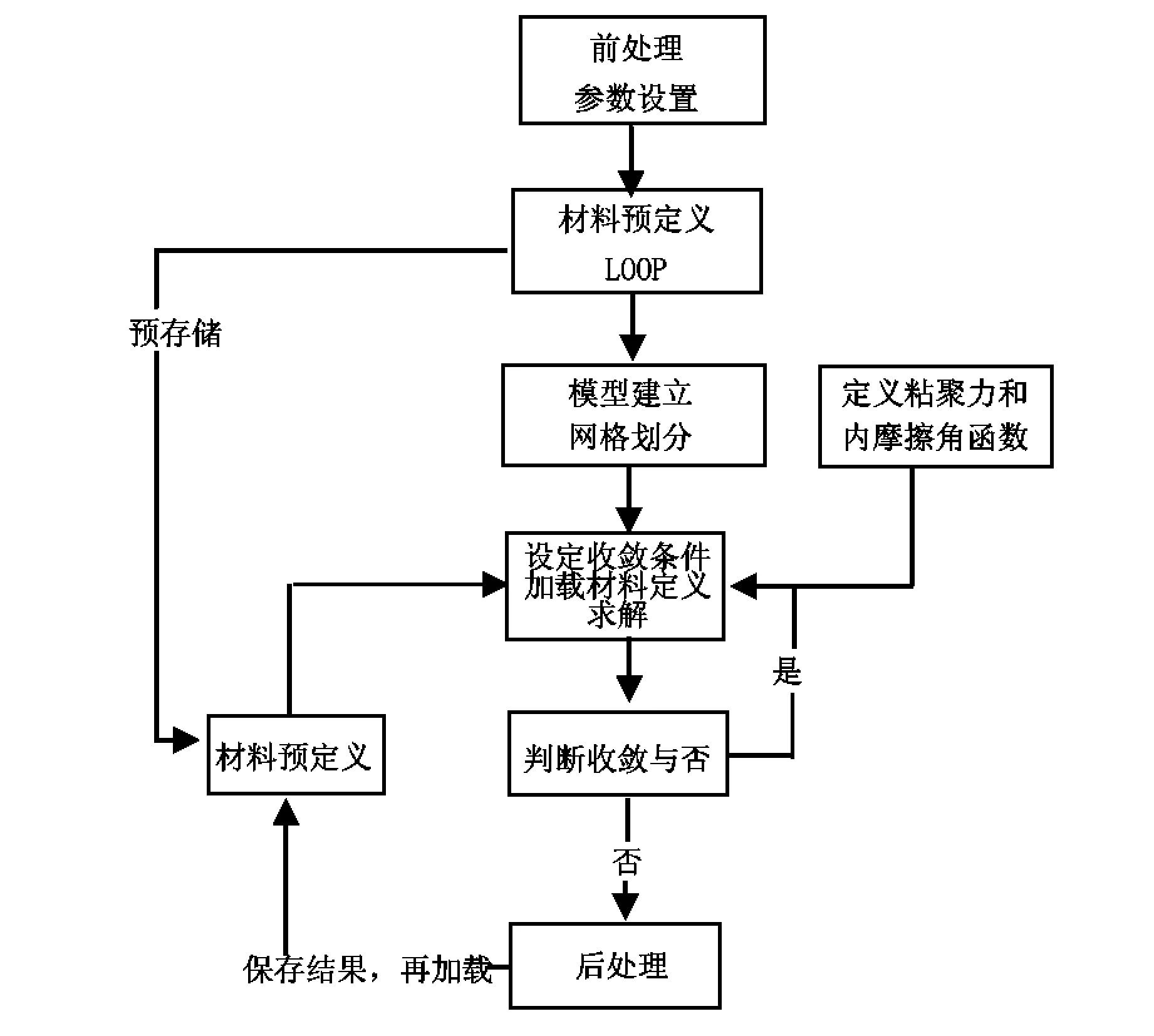
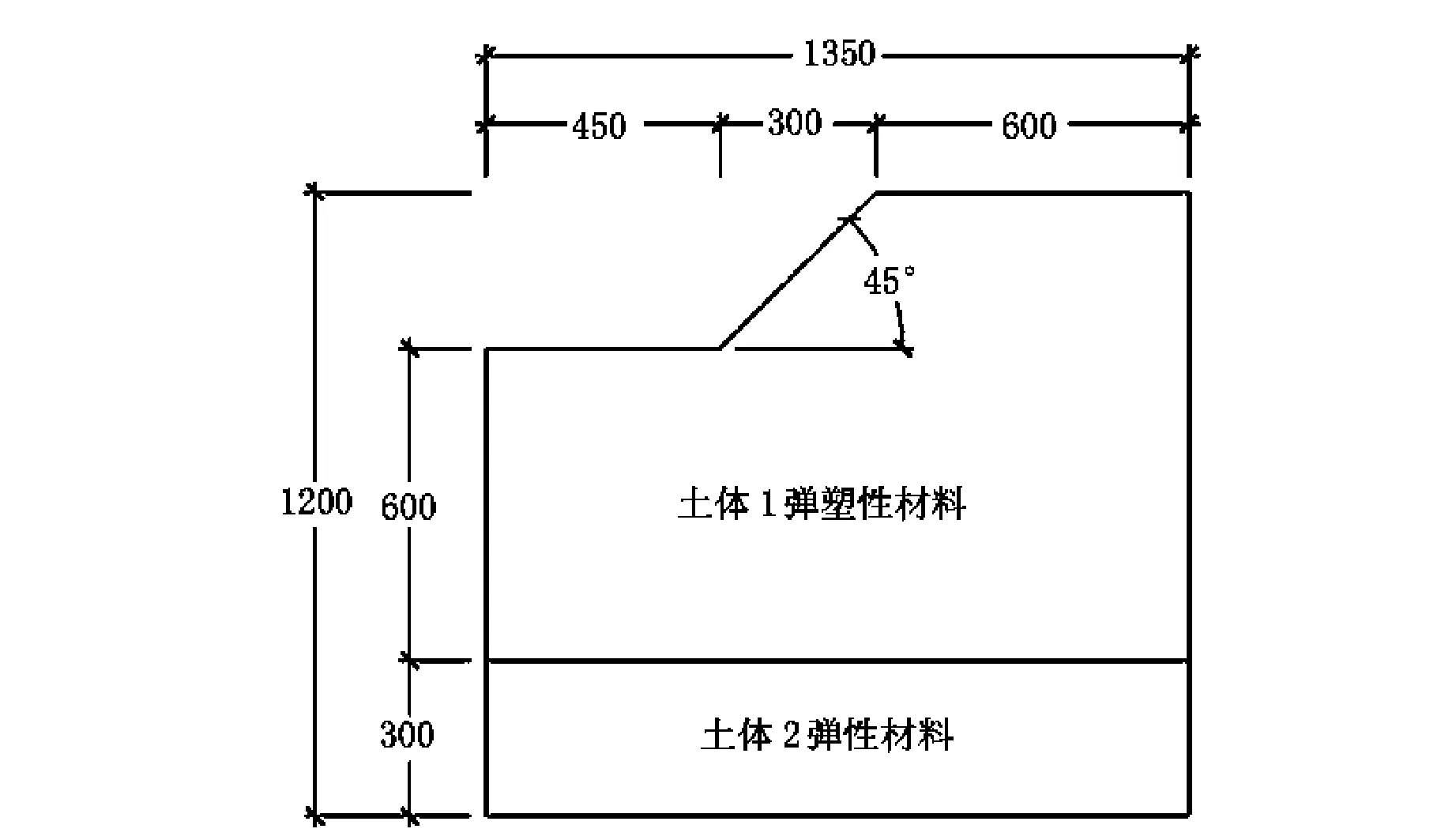
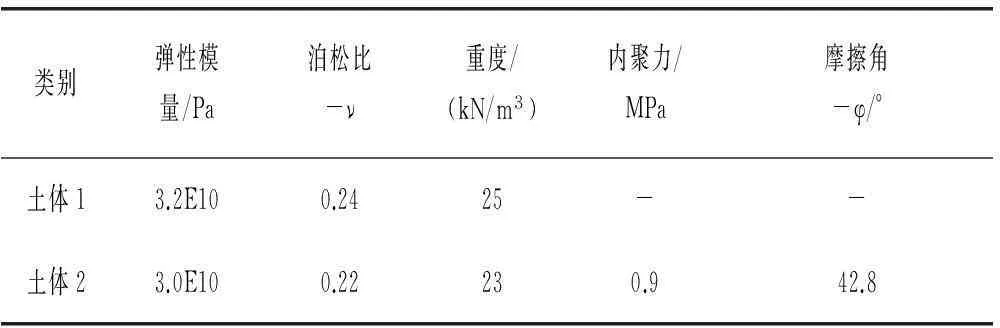
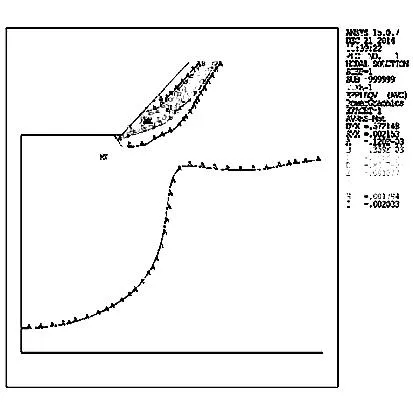
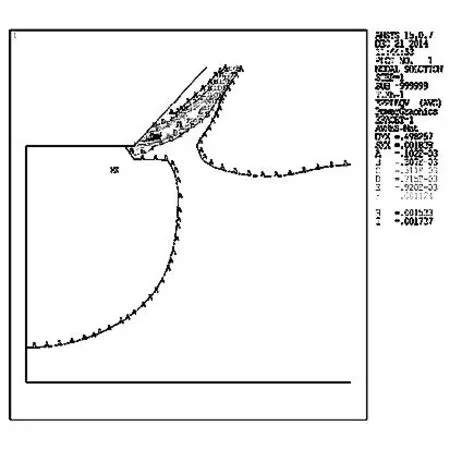
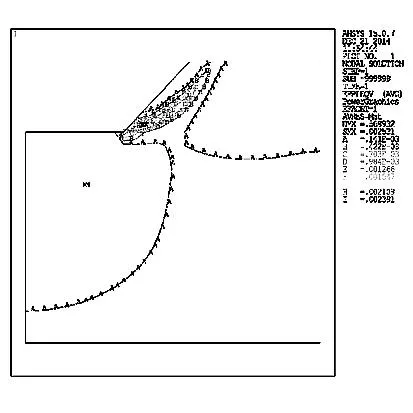
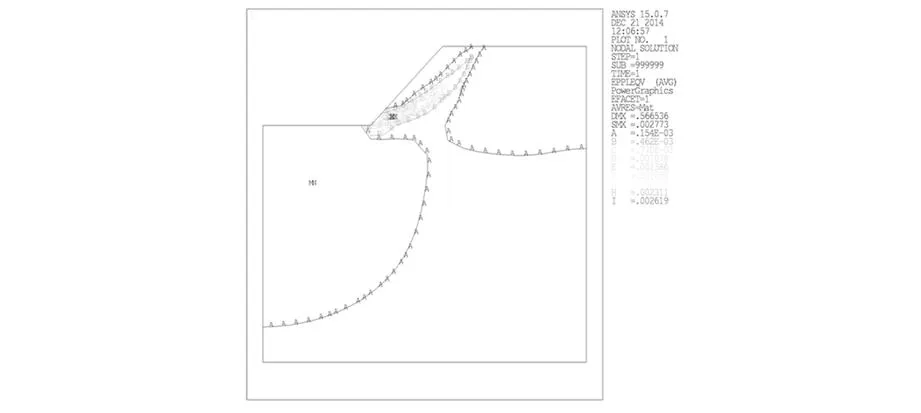
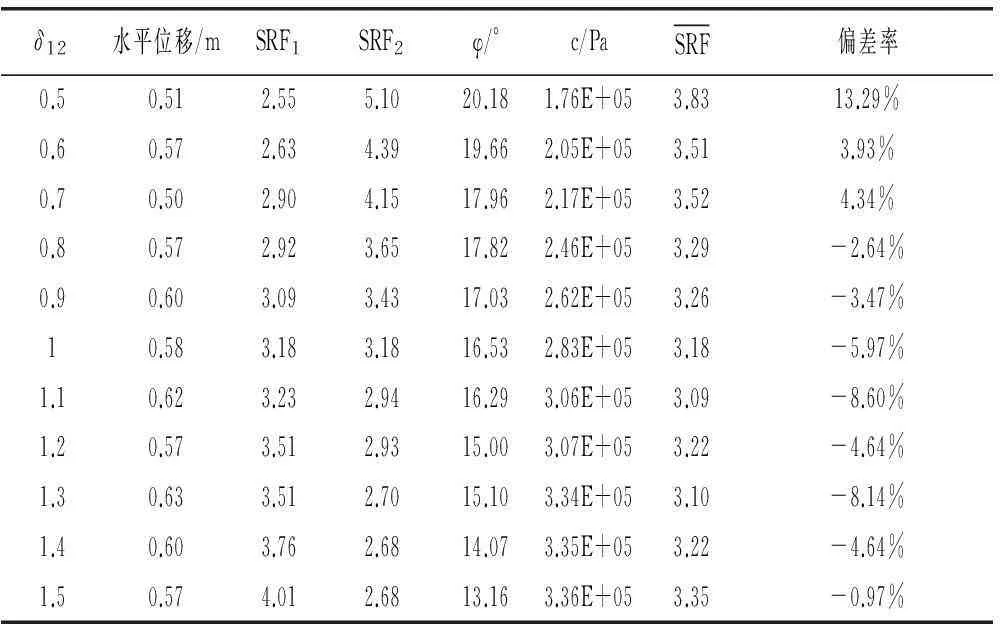
其折减系数的大小是依据不同的衰减速度和衰减程度以及其内在的力学机制决定的。一般情况下，粘聚力衰减快，内摩擦角衰减慢，SRF1小，此时，按SRF1

2ANSYS传统强度折减系数法分析边坡稳定性流程

ANSYS用传统强度折减法分析边坡稳定的一般流程为：首先选取合适的折减系数，将折减后的参数(c、φ)作为程序输入值，若程序算法收敛，则在该折减后的边坡仍处于稳定状态，此时继续将现状态下的边坡参数用折减系数进行折减，继续作为输入值输入程序，重复上述验证过程，直至程序恰好不收敛，则此时理论上可以认为该边坡已达到极限状态，该状态下的折减系数可视为该边坡理论上的稳定或安全系数。上述过程可如图1所示。

3双系数强度折减系数法有限元分析的实现

为更好明确内摩擦角φ的折减系数与粘聚力c的折减系数间关系，现引入折减比δ12，见式(2)

(2)

图1　边坡分析流程图

结合式(1)得

(3)

综上，即可得双折减系数理论于有限元分析的一般流程，见图2。

图2　双折减系数法有限元分析分析流程图

通过对在一定区间赋值可得到与其一一对应的边坡极限状态的结果，将其与极限平衡理论的Bishop simplified的结果对比，可得到较为合理的的取值。

4算例

以某矿边坡为例，考虑到要表现实际土体的塑性发展和应力分布，以及还要消除边坡影响土体边界效应，故将其分成上下两层，上层设为弹塑性材料，下层设为塑性材料。这样可较好的模拟改边坡的变形和塑性区的变化。

边坡尺寸如图3，边坡参数见表1。

图3　边坡示意图(m)

类别弹性模量/Pa泊松比-ν重度/(kN/m3)内聚力/MPa摩擦角-φ/°土体13.2E100.2425--土体23.0E100.22230.942.8

根据对于折减比δ12，取区间[0.5,1.5]上的值，采用有限元双折减系数法进行计算，可得其一一对应的内摩擦角的折减系数与粘聚力的折减系数，且与Bishop simplified的偏差对比，分析结果见图4～图8。

图4　塑性应变图

图5　塑性应变图

图6　塑性应变图

图7　塑性应变图

由图4～图8分析可得，随着折减比不断增加，边坡失稳时，塑性区贯通至坡顶，表明此时边坡已经发生破坏，且破坏区底部位置变化不明显，贯通至坡顶塑性发展区域发展变化，呈现塑性去收缩的态势。

图8　塑性应变图

δ12水平位移/mSRF1SRF2φ/°c/PaSRF偏差率0.50.512.555.1020.181.76E+053.8313.29%0.60.572.634.3919.662.05E+053.513.93%0.70.502.904.1517.962.17E+053.524.34%0.80.572.923.6517.822.46E+053.29-2.64%0.90.603.093.4317.032.62E+053.26-3.47%10.583.183.1816.532.83E+053.18-5.97%1.10.623.232.9416.293.06E+053.09-8.60%1.20.573.512.9315.003.07E+053.22-4.64%1.30.633.512.7015.103.34E+053.10-8.14%1.40.603.762.6814.073.35E+053.22-4.64%1.50.574.012.6813.163.36E+053.35-0.97%

5结论

(2)双折减系数理论的有限元分析，对于偏岩质边坡，抗剪强度参数内摩擦角φ的折减系数的取值小于粘聚力c的折减系数的取值，得到较为合理的分析结果。

参考文献：

[1]赵尚毅,郑颖人,时卫民,等.用有限元强度折减法求边坡稳定安全系数[J].岩土工程学报,2002,24(3):343-346.

[2]郑颖人,赵尚毅.岩土工程极限分析有限元法及其应用[J].土木工程学报,2005,38(1):91-99.

[3]董天文，郑颖人. 桩基础双折减系数有限元强度折减法极限分析[J].岩土力学，2011，10：,2011,32(10):3148-3154.

Application of finite element method of double reduction coefficient method for slope stability

ZOU Xi-xuan,ZHANG Jun-ping

(College of Architecture and Survey Engineering, Jiangxi University of Science and Technology, Ganzhou, Jiangxi 341000，China)

Abstract:Through the design of slope stability analysis program by double reduction factor method based on finite element analysis, the author analyzes the slope stability of one-side slope. The conclusion is that with the gradual increase of angle of internal friction reduction factor, cohesive force reduction factor decreases; slope instability appears when the plastic zone in the top trend gradually shrinks. The plastic damage zone in slope shows a gradual contraction when the slope loses stability.

Keywords:double reduction factors; slope stability analysis; plastic damage

中图分类号：U416.1

文献标识码：C

文章编号：1008-3383(2016)03-0010-02

作者简介：邹希煊(1991-)，男，全日制硕士研究生。

收稿日期：2015-07-29