预估火炸药寿命的数学模型及其计算

刘子如，邵颖惠，任晓宁，常　海

(西安近代化学研究所，陕西 西安，710065)



预估火炸药寿命的数学模型及其计算

刘子如，邵颖惠，任晓宁，常海

(西安近代化学研究所，陕西 西安，710065)

摘要：评论了预估火炸药及其制品的安全贮存寿命、使用寿命和可靠贮存寿命的数学模型和计算方法，包括常用的Arrhenius方程、Berthelot方程和温度系数方程及修正的Arrhenius方程、加速因子方程、多应力因素的Eyring方程、交变老化温度的累积损伤模型、BP神经网络法、结构寿命和可靠寿命的预估方法等。提出了简单快速的点斜法和单温度定时法，认为可以通过失效概率的所谓界限模型计算火炸药及其制品的可靠性和可靠贮存寿命。比较了一些计算方法，给出了Arrhenius方程和Berthelot方程预估寿命相等的条件，指出了这些方法或方程的使用范围，并举例说明了一些模型和计算方法的实际应用。附参考文献30篇。

关键词：物理化学；火炸药；寿命预估；寿命计算方法；安全寿命; 使用寿命；可靠贮存寿命

引 言

火炸药的寿命是安全贮存和正常使用的重要指标,可以分为安全贮存寿命和安全使用寿命。由于火炸药及其制品对配方、生产工艺、贮存运输使用的环境温湿度条件等因素相对敏感，因此其性能参数具有明显的波动性，同时由于测试人员、测试方法及取样的不同都会带来性能参数测试数据的散布和不确定性，因此以性能参数退化为依据而预估的寿命具有随机性，即预估的寿命存在可靠度的问题。可靠贮存寿命(或可靠寿命)是规定可靠度下的贮存寿命。可靠度是能够完成使用(贮存)寿命期内技术要求的概率。

加速老化预估寿命涉及到3个重要方面或3个步骤：(1)试验条件的选择；(2)跟踪测试参量(失效模式)及失效判据的确定；(3)外推到常温或使用温度的依据—失效参量退化的时间关系和退化率的温度关系。本文仅就加速老化预估寿命的第3步骤，即预估寿命温度关系的数学模型和计算方法作一些评述。

1常用预估寿命三方程的比较

1.1Arrhenius方程

Arrhenius(阿伦尼乌斯)方程是常用于预估火炸药及其制品贮存寿命的方程。其对数形式为

(1)

如果加速试验可以直接获得老化临界寿命值τ，则可不通过反应速率(或性能退化率)常数进行常温下的寿命预估。用下列形式的Arrhenius方程就可以预估寿命：

lnτ=lnZ+E/RT

(2)

或

lgτ= lgZ+E/2.303RT

(3)

式中：Z为方程(1)中指前因子A的倒数，即Z=1/A。

该方程虽然是化学动力学方程，由化学反应引起的性能变化用该方程外推寿命是毫无疑问的，但理论推导和试验都证明，该方程也同样适用于预估力学性能、迁移和扩散等物理过程所引起的寿命变化。但应用该方程时应该注意以下问题：(1)老化是通过测定反应速度而获得，对于扩散和各种类型的应力作用，该方程有时被限制使用；(2)试验温度与外推温度间隔较小，可认为活化能与温度无关，这时它才正确；(3)该方程有时很难考虑到如湿度、氧和腐蚀性气体导致的叠加效应。若老化中同时存在几种影响性能的变化过程，则它们的活化能必须是相同或近似相等。

1.2Berthelot方程

Berthelot(贝瑟洛特)方程是除Arrhenius方程外另一个重要的老化寿命外推方程。其基本形式是

T=Ab+B·lgτ

(4)

此方程是描述老化寿命与温度的关系，不需要获得反应速率常数或性能变化速率(或称为退化率)，即不需要知道反应或性能随老化时间变化的规律，只要测出各个老化温度下的临界寿命，就可以外推预估寿命。因此，与Arrhenius方程相比，Berthelot方程可以简化试验和数据处理过程，通常由其外推获得的寿命小于Arrhenius方程，更接近实际寿命。因此被普遍应用于火药安全贮存寿命的预估，在相应的国军标[1-2]中已被规定为数据的处理方法。

1.3温度系数方程

温度系数方程是从Arrhenius方程推导出来的近似公式，用来计算每升高或降低10℃时性能变化速率(退化率)的比率。其表示式为

(5)

式中：T1和T2分别为外推贮存温度和加速老化温度；τ1和τ2分别为温度T1和T2下的贮存寿命；γ为温度系数。

实际上，该方程也是简化的Berthelot方程，因为温度系数可以按公式γ=10-10/B计算，而其中的B值就是Berthelot方程(4)中的B值。

由于许多变化过程的活化能(E)范围为120～160kJ/mol，其温度系数均为3左右。因此，进行寿命预估时只要通过单温度的试验获得该老化温度的寿命(τ2)，用经验获得温度系数(γ)，就可以由式(5)计算获得外推温度下的寿命(τ1)。

1.4简化试验和计算的点斜法及单温度定时法

点斜法是单一温度老化获得的性能失效时间或寿命临界点，用已知或另外途径获得的活化能(E)作为斜率，根据Arrhenius方程(式(2))外推获得贮存寿命，因此称为点斜法。其实际上是Arrhenius方程(式(2))的简化应用，其中活化能(E)就是斜率，只是E可以通过其他途径获得，只要其是描述同一失效模式和机理的温度系数。显然该方法要比Arrhenius方程外推获得贮存寿命简单得多，老化试验量也少得多，获得寿命临界点时也可以不考虑过程。

单温度定时法实际上是从温度系数方程简化而来。当温度系数已知时，就可以用该方法确定预期寿命在单温度下的老化时间。方程的基本形式为

τ2=Ae-kT2

(6)

式中：A=τ1γ0.1T1，k=0.1·lnγ。

当温度系数γ和外推温度T1确定时，则可以分别计算外推贮存温度T1下贮存寿命为τ1时的A和k值，当加速老化温度为T2，外推寿命为τ1时，由式(6)计算加速老化到达寿命临界点时所需的老化时间τ2。因此，仅进行某一温度T2下的加速老化试验，当试样经历老化仍未失效的时间等于或大于τ2时，则认为该试样的外推寿命等于或大于τ1。

单温度定时法适用于已知温度系数材料的例行快速检测和剩余寿命的快速预估。

1.5三方程老化预估寿命相等的条件

通常用Arrhenius方程外推获得的预估寿命会大于温度系数法和Berthelot方程法。但在一定条件下，前者与后者外推获得的预估寿命就会相等或接近。

根据推导，Arrhenius方程与温度系数法和Berthelot方程预估寿命相等的条件分别是：

(7)

(8)

或

B= (T-Ab)/( lgZ+E/2.303RT)

(9)

可见，预估寿命相等的条件，既与活化能(E)有关，也与外推温度(T1)和加速老化温度(T2)有关。

2其他安全贮存寿命预估方法

2.1修正的 Arrhenius方程

Arrhenius方程通常假设指前因子和表观活化能是与温度无关的常数，但从过渡态理论或碰撞理论都可推导出其均与温度有关。研究表明[3]，指前因子大致与温度(T)的m次方有关，因此Arrhenius方程被修正为三参数方程

(10)

用修正的Arrhenius方程处理性能变化的温度关系，预估老化寿命的结果有时会更接近实际。

2.2加速因子方程

加速因子方程是关联加速老化寿命与贮存温度寿命之间关系的方程。经不同贮存时间后火炸药及其制品在加速老化时有不同的失效时间或寿命临界点，寿命加速因子(KT)被定义为常温已贮存的年限差(Δy)与加速老化试验的失效临界点时间差(Δm)(月)的比值[4]，即

(11)

式中：加速因子(KT)表示试样在高温下贮存一个月相当于在常温下贮存的时间(年)。计算剩余使用寿命(ys)和总使用寿命(yg)方程分别为ys=KT·m和yg=KT·m+y，其中，m为高温加速试验的失效临界点时间(月)；y为常温下已贮存的时间(年)。

某固体火箭发动机双基推进剂的已贮存时间和老化获得的失效时间，以及通过式(11)计算得到的KT和计算的ys和yg，列于表1[4]。

表1　某双基推进剂装药老化加速因子和使用寿命的计算结果

2.3Eyring方程

在预估多应力因素作用下火炸药的老化寿命或Arrhenius方程不适用时，则可用Eyring方程[5-7]，该方程如下

(12)

式中：L(V)为与应力因素有关的寿命；V为应力因素，如热应力-温度，也可以是非热应力，如湿度；A和B为方程待定常数。

式(12)也可表示为

L=A′T-1eB/T

(13)

式中：A′=e-A；T=V，为绝对温度。

若以寿命τ形式表示修正的Arrhenius方程，则式(10)可以表示为

τ=ZT-meE/RT(其中Z=A-1)

(14)

式(14)与式(13)非常相似，可以认为Eyring方程(式(13))是修正的Arrhenius方程(式(14))的一种特殊形式，两者不同之处是式(14)中温度T的幂指数m为1，而式(13)中B=E/R。

与Eyring方程类似的有温度-非温度(T-NT)模型，这是考虑除了温度的应力外，还有一个非温度应力U的寿命方程

L(T,U)=A′T-1U-neB/T

(15)

式中：U为温度以外的应力，如相对湿度；A′、B和n为待定常数。

还可以把湿热加速老化预估寿命的Eyring方程写为下列形式

(16)

当湿度U恒定，温度T为可变量时，令A′=AU-1eB/U为常数，则从式(16)可得L=A′T-1eC/T，即与式(13)相似。

一般认为，Arrhenius方程和式(12)所表示的Eyring方程适用于单一温度应力下的加速老化模型，而式(15)和式(16)所示的Eyring方程更适用于双应力因素(如湿热)加速老化的预估模型。

2.4交变老化温度的累积损伤模型

环境应力不可恢复性的不可逆作用，每次都会给产品带来损伤，这些损伤累积起来超过某一临界值时，材料就会发生故障或失效，描述这种变化过程的模型就是累积损伤理论(Cumulative Damage Theory)[8]。

假定在特定的交变应力li的作用下，平均可承受的循环次数(寿命)为Ni，而循环次数为ni，则Miner法则认为，当

(17)

被满足时，就可认为材料到达平均使用寿命(MTTF)。应用累积损伤模型的前提是，即使应力大小变化，失效机理也不变。

如果环境温度变化是时间的连续函数T=f(t)，而老化寿命的温度函数L=F(T)，认为在微小时间段Δti内温度保持为Ti，把Miner法则方程中的循环次数用实际的时间代替，即ni=Δti，而Ni=L(Ti)，则式(17)可写为

(18)

(19)

若老化寿命的温度函数L(T)是Arrhenius方程(2)或Eyring方程(13)，则式(19)可写为

(20)

或

(21)

根据已知参数，如Arrhenius方程的参数Z和E或Eyring方程的参数B和A′，以及温度的时间函数T=f(t)，求解式(20)或式(21)的积分方程，即可获得变化环境下的平均寿命MTTF[6-7]。

文献[7]中应用此方法得出某固体火箭发动机装药经过14d的高温运输后，贮存寿命缩减了约15个月。

2.5神经网络法

人工神经网络(Artificial Neural Network，简称ANN)是20世纪80年代发展起来的综合性学科， ANN通过网络学习实现非线性函数映射，广泛应用于性能预测、模式识别、模糊控制、图像识别等过程。其中BP网络是一种应用十分广泛的人工神经网络，BP的重要功能之一是非线性函数映射。根据Kolmogorov定理，总是存在一个三层神经网络，能精确实现任意的连续映射[9-10]。BP神经网络一般由输入层、隐含层和输出层构成。输入层神经元的输入信息必须是对输出具有典型影响的因素，网络相邻层间的神经元是互连的，同层神经元之间不相连，邻层互连神经元间存在可调权值。使用前需采用数据对其进行训练。

火炸药及其制品的寿命问题往往是多因素、非线性问题，通常的单因素分析方法或多元回归分析方法无法准确研究这类问题，而BP神经网络模型是处理这类问题的有效方法。国内刘沃野等[11]利用BP神经网络法对某库存枪弹的贮存寿命进行了预估。有研究者[12-13]提出利用遗传算法(GA)和神经网络相结合的遗传神经网络(GA-BP)模型，预测推进剂使用贮存寿命或可靠贮存寿命，可以克服BP算法的不足。GA是模拟生物进化过程的全局性概率搜索算法，具有自适应性、全局优化性和隐含并行性。GA可以优化BP神经网络结构、权值和阈值。两者结合可以建立较好地预估寿命遗传神经模型。

3推进剂药柱结构完整性的寿命预估

3.1通过动态力学性能预估寿命

结构完整性是固体火箭发动机寿命的决定因素，测定力学性能退化是间接分析结构完整性的寿命评估方法。动态黏弹法或动态力学性能分析法(DMA)研究固体推进剂的贮存寿命时，在一定程度上可以避免采用单轴拉伸、应力松弛和蠕变研究推进剂老化带来的问题，即材料大变形引起分子链滑移的物理变化与化学变化混杂在一起的缺陷。因此动态黏弹试验或DMA中的模量变化更能准确真实地反映固体推进剂的热老化过程。各种动态模量的退化率都可以定义为老化速率(μ)。此外，更因为黏弹性材料的物理老化过程应考虑时间或频率的影响，动态力学性能恰好考虑了这种因素[14]。

由于DMA试验或动态黏弹试验是在程序升温下获得动态力学性能数据，因此其还有一个特点是可通过WLF方程(时温等效方程)得到动态力学性能变化(物理老化)的活化能(Ea)，有可能从一个老化温度试样的DMA试验就可以建立力学性能随温度变化的数学模型，节省了很多时间。同时，还可以通过动态模量或柔量主曲线的变化规律的分析获得力学性能的失效判据。这样就可以通过点斜法或温度系数方程进行寿命评估，可大大简化老化试验和计算。

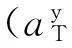
3.2利用黏弹体有限元方法分析结构完整性

基于黏弹体有限元方法的推进剂结构完整性分析，该方法要有比较完善的三维有限元分析软件和复杂的计算。袁端才等[16]基于加速老化和三维黏弹性有限元分析，预估了某固体火箭发动机装药的贮存寿命，得到推进剂装药在20℃下的贮存寿命为13.8年。

3.3从初始气孔率和NG的迁移预估贮存寿命

由于双基或改性双基推进剂药柱的缓慢分解产生的气体和NG的迁移在双基推进剂药柱中形成空隙或微裂纹，随老化时间和温度而增多和增大。当老化到达一定时间后初始气孔率急剧增大，这时黏弹体发生了蠕变，药柱结构完整性被破坏，推进剂药柱失效。可以通过测定老化温度TH下初始气孔率急剧变化的时间tH，该时间即为失效时间，利用温度系数方程预估推进剂药柱的贮存寿命[17]。

研究表明[14,18]，增塑剂NG向包覆层(或隔热层、阻燃层)迁移是自由装填式双基或改性双基推进剂的主要失效模式，因为饱含NG的包覆层会造成开裂、脱粘等破坏药柱结构完整性的现象，也可能使隔热层或阻燃层失去作用，使燃烧不稳定，导致火箭发动机失效，甚至发生事故。文献[14，18]通过加速老化测定NG在包覆层中的迁移，预估了某自由装填式双基推进剂的老化寿命。

4可靠贮存寿命的预估

4.1计算失效概率的两种模型

预估可靠寿命必须计算失效概率，通常最常用的计算失效概率有界限模型和应力-强度干涉模型。

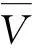
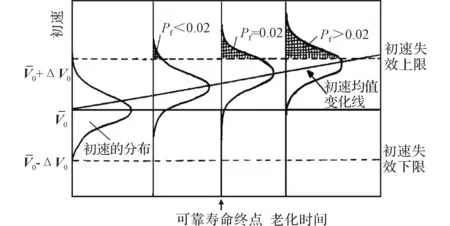
图1　某发射药失效概率老化时间关系示意图 Fig.1　Schematic diagram of the relationship between the failure probability and aging time for gun propellant

应力-强度干涉模型是研究装药的环境应力与所能承受的强度之间的关系，当前者超过后者即视为失效。如经过环境条件、失效模式和判据、应力和材料性能等一系列的分析后，获得图2所示的一系列随时间变化的Warner图，即应力-强度干涉原理图。这是设计技术要求(来自应力分析)和材料能力(来自失效分析或强度分析)的概率分布随时间变化的一系列曲线。两种分布曲线尾部重叠部分的大小，即表示失效概率的大小。

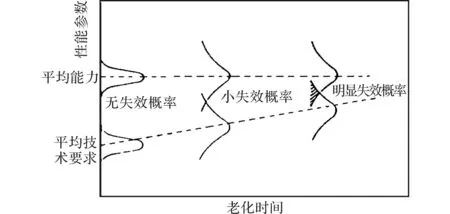
图2　失效概率随时间变化的Warner图Fig.2　Warner diagrams for failure probability versus time variation

现今给予上述强度与应力更广泛的定义：凡是阻止产品失效的因素，都可称为强度，而凡是引起产品失效的因素，都称为应力。

4.2可靠贮存寿命预估模型

正态分布与对数正态分布是可靠性研究中常用的两种寿命分布模式，适用于描述受物理化学过程所支配的失效概率。余文力等[20]研究了某导弹战斗部装药的可靠贮存寿命，得出该炸药装药各老化温度下的贮存寿命服从对数正态分布，并计算得到不同置信度下的贮存寿命置信下限。刘子如等[21]对FH-94复合固体推进剂的可靠度和可靠贮存寿命进行了研究，经老化和力学性能测定，通过数据的正太分布分析，计算得到一定置信度和可靠度下限下的可靠贮存寿命。

研究表明[22-23]，推进剂及火工品的贮存寿命服从Weibull分布。分布曲线起点为坐标原点(位置因子x0=0)时，则三因子Weibull分布退化为只有尺度因子(α)和形状因子(β)的两参数的分布函数

(22)

蒙特卡罗(Monte Carlo)法也称为统计试验方法，其是可靠性模拟计算的基础方法，用于处理随机变量问题。其理论基础是概率论中的基本定律，即大数定律，是将随机变量赋予适当的物理含义，并将各数随机变量概率特性与数字分析问题的解答联系起来。Monte Carlo法实际上是用计算机进行模拟计算。刘兵吉[24]对固体推进剂随环境温度变化的力学性能进行Monte Carlo模拟计算，除自然变量时间外，把其他变量均视为随机变量，在计算机上产生随机数，经统计模拟处理，发现延伸率的分布函数为Weibull分布，从而计算获得了HTPB推进剂不同可靠度下的寿命。

4.3弹药可靠贮存寿命的预估方法

弹药是包括火炸药的多部件的体系，其可靠性是系统可靠性，因此可靠性的预测是一个复杂的系统工程，而且这些评估方法都有较复杂的数学和概率统计学问题，评估方法有： Bayes评估法[25-26]，Poission过程评估法[27]，无失效数据的样本空间排序法[28]，有无寿命数据的估计法[29]，灰色预测法[30]等。这些方法基本上都是适用于弹药的小样本量、成败型的可靠性及可靠寿命分析，这与上述火炸药及其制品可靠贮存寿命的评估不同，后者是以影响使用或影响安全贮存的性能变化(退化)超过某一规定的指标为失效判据，而不是成败型。

5结束语

(1)预估火炸药及其制品的安全贮存寿命、使用寿命和可靠贮存寿命，需要根据贮存环境条件和(或)使用条件，选择合适的老化数学模型和计算方法。

(2)预估安全贮存寿命通常用Berthelot方程或温度系数方程；多应力因素导致的老化寿命宜用Eyring方程；交变应力作用下老化寿命的预估建议采用累积损伤模型；预估已知活化能或温度系数或加速因子的火炸药老化寿命或剩余寿命，可以分别采用简单快速的点斜法或单温度定时法或加速因子方程法。BP神经网络法适用于预估已有相当数量的(贮存和使用)数据，而导致性能失效因素的温度和时间关系难于用数学模型描述的火炸药老化寿命。

(3)结构寿命需要首先分析造成火炸药制品结构完整性的失效因素，之后采用适当的方法预估老化寿命。

(4)火炸药的可靠性和可靠贮存寿命可以通过失效概率的界限模型进行预估。

参考文献：

[1]GJB 772A-1997火药试验法506.1 预估火药安全贮存寿命—热加速老化法[S]. 1997.

[2]GJB 770B-2005火药试验法505.1安定性、相容性和预估安全贮存寿命—热减量法[S]. 2005.

[3]赵学庄. 化学反应动力学原理(上册)[M]. 北京：高等教育出版社，1984.

[4]李兆民. 固体火箭发动机使用寿命的确定[J]. 推进技术，1989, 1(4)：50-55.

LI Zhao-min. Determination of service life of solid rocket motor [J]. Chinese Journal of Propulsion Technology, 1989, 1(4)：50-55.

[5]Reliasoft Company. Accelerated Life Testing Analysis Reference[M]. ReliaSoft: ReliaSoft Corporation, 2004.

[6]王玉峰，李高春，王晓伟. 固体火箭发动机海洋环境下的贮存及寿命预估 [J]. 火炸药学报，2008，31(6)：87-90.

WANG Yu-feng, LI Gao-chun, WANG Xiao-wei. Storage and life prediction of solid rocket motor in sea environment [J]. Chinese Journal of Explosives and Propellants, 2008, 31(6)：87-90.

[7]王 斌，常新龙. 固体火箭推进剂贮存使用寿命的累积损伤—反应论模型[J].弹箭与制导学报, 2007, 27(1)：171-173.

WANG Bin, CHANG Xin-long. The cumulative damage-reaction theory life model to the storage and usage of solid rocket propellant [J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2007, 27(1)：171-173.

[8]Chaitanya S S, Mahendra J P, Madhav V P. Accelerated aging and life time prediction analysis of polymer composites: a new approach for a realistic prediction using cumulative damage theory [J]. Polymer Tesing , 1994, 13: 295-322.

[9]Hush D R, Horne B G. Progress in supervised neural networks [J]. IEEE Signal Processing Magzine, 1993 (1)：8-39.

[10] 罗发龙，李衍达. 神经网络—信号处理 [M]. 北京：电子工业出版社，1993.

[11] 刘沃野，蒙占海. 基于神经网络的库存枪弹储存寿命预测研究[J]. 军械工程学院学报，2001，13(3)：12-15.

LIU Wo-ye, MENG Zhan-hai. Reseach on forecasting stock life of storage bullets by neural network [J]. Chinese Journal of Ordnance Engineering College, 2001，13(3)：12-15.

[12] 莫文宾，李进贤. 基于遗传神经网络的NEPE推进剂贮存寿命预估[J]. 火炸药学报，2009，32(5)：58-61.MO Wen-bin, LI Jin-xian. Life prediction of NEPE propellant base on GA-BP neural network [J]. Chinese Journal of Explosives and Propellants, 2009，32(5)：58-61.

[13] 李进贤，莫文宾，唐金兰. 固体推进剂力学性能预估研究[J]. 计算机仿真，2011，28(1)：76-79.

LI Jin-xian, MO Wen-bin, TANG Jin-lan. Research on mechanical property prediction of solid propellant base on GA-BP neural network [J]. Chinese Journal of Computer Simulation, 2011，28(1)：76-79.

[14] 刘子如. 含能材料热分析[M]. 北京：国防工业出版社，2008.

[15] 张腊莹，刘子如，衡淑云，等. NEPE类推进剂的寿命预估[J]. 推进技术，2006，27(6)：572-576.

ZHANG La-ying LIU Zi-ru, HENG Shu-yun, et al. Estimation of life span for NEPE propellant [J]. Chinese Journal of Propulsion Technology, 2006，27(6)：572-576.

[16] 袁端才，唐国金，李海阳，等. 基于加速老化与三维粘弹性有限元分析的固体导弹发动机寿命预估[J]. 兵工学报，2006，27(4)：685-689.

YUAN Duan-cai, TANG Guo-jin, LI Hai-yang, et al. Three-dimension viscoelastic analysis and accelerated aging approach to predict the service life of solid missie motor [J]. Chinese Journal of Acta Armamentarii, 2006，27(4)：685-689.

[17] GAO Ming, CAI Ti-min. Content rate and its application—a new method for prediction storage life of solid propellant grain [J]. Chinese Journal of Propulsion Technology, 1999，20(5):99-103.

[18] Heng S Y, Pan T X, Kong Y H, et al. The Nitroglycerin content distribution in the coating of the solid propellant and the service life prediction of the charge [J]. Propellants, Explosives, Pyrotechnics, 1991, 16 :31-35.

[19] 刘子如，衡淑云.预估发射药可靠寿命的加速老化试验方案[C]//火炸药可靠性技术研讨会文集.西安：西安近化化学研究所，1991:271-280.

[20] 余文力，董三强，朱满林，等. 导弹战斗部炸药装药的贮存可靠性研究[J]. 空军工程大学学报(自然科学版)，2005，6(2):43-45.

YU Wen-li, DONG San-qiang, ZHU Man-lin, et al. Research on storge reliability of missile warhead explosive charge [J]. Chinese Journal of Air Force Engineering University (Natural science edition), 2005，6(2):43-45.

[21] 刘子如，郝仲璋，谢俊杰，等. FH-94复合固体推进剂的可靠度评估和可靠贮存寿命预测研究[J]. 兵工学报(火化工分册)，1994(2)：24-27.

LIU Zi-ru, HAO Zhong-zhang, XIE Jun-jie, et al. Research on the evaluation of reliability and prediction of reliable storge life for FH-94 solid propellant [J]. Chinese Journal of Acta Armamentarii (the Fascicule of Explosives and Propellants), 1994(2)：24-27.

[22] 杨 根. N-15B推进剂热老化特性与贮存寿命预估研究[D]. 长沙：国防科学技术大学，2005.

[23] 郑 波，张国安. 自然贮存环境下弹药系统贮存可靠性评估[J]. 质量与可靠性，2003(3)：22-25.

ZHENG Bo, ZHANG Guo-an. Storage reliability assessment of ammunition system under natural storage [J]. Chinese Journal of Quality and Reliability, 2003(3)：22-25.

[24] 刘兵吉. 固体推进剂贮存可靠寿命的Monte-Carlo仿真计算[J]. 推进技术，1992 (2)：68-71.

LIU Bing-ji. Carlo monte simulation calculation of solid propellant storage life [J]. Chinese Journal of Propulsion Technology, 1992(2)：68-71.

[25] 党晓玲，武小悦，沙基昌. 先验信息在Bayes可靠性评估中的应用研究[J]. 系统工程，1998, 16(6)：54-56.

DANG Xiao-ling, WU Xiao-yue, SHA Ji-chang. A research to prior information used in Bayes reliability evalution [J]. Chinese Journal of Systems Engineering, 1998, 16(6)：54-56.

[26] 陶 敏，潘文庚，潘火荣.库存弹药可靠性鉴定的新方法探讨[J]. 弹箭与制导学报，2000(2)：43-46.TAO Min, PAN Wen-geng, PAN Huo-rong. The research of new-style ammunition reliability test method with checking and accepting [J]. Journal of Projectiles, Rockets, Missiles and Guidance. 2000(2)：43-46.

[27] 郑 波，许和贵，姜志保. 一种基于Poission过程的弹药贮存寿命评估方法[J]. 兵工学报，2005, 26(4)：528-530.

ZHENG Bo, XU He-gui, JIANG Zhi-bao. An estimation method of ammunition storge life based on Poisson process [J]. Chinese Journal of Acta Armamentarii, 2005, 26(4)：528-530.

[28] 李东阳，孙德宝. 排序法在某类弹药寿命分析中的应用研究[J]. 军械工程学院学报，2003，15(3)：29-32.

LI Dong-yang, SUN De-bao. Application of arrange seguence method in some ammunition′s storge life analysis[J]. Chinese Journal of Ordnance Engineering College, 2003，15(3)：29-32.

[29] 李长福，夏建中，黄跃德，等. 考虑删失数据时弹药贮存可靠性评估方法研究[J]. 兵工学报，1996, 17(4)：301-304.

LI Chang-fu, XIA Jian-zhong, HUANG Yue-de，et al. Study on the method of storage reliability evaluation of ammunition in consideration of censored data [J]. Chinese Journal of Acta Armamentarii, 1996, 17(4)：301-304.

[30] 王志军，王瑞臣，蔡汉文，等. 弹丸失效规律及有效贮存期预测研究 [J]. 北京理工大学学报，1998, 18(4)：449-452.

WANG Zhi-jun, WANG Rui-chen, CAI Han-wen, et al. A study on characteristics of loss of efficacy and the storge period of validity of warheads [J]. Chinese Journal of Transactions Beijing Institute of Technology, 1998, 18(4)：449-452.

Mathematical Models and Its Calculations for Predicting the Life of Explosives and Propellants

LIU Zi-ru，SHAO Ying-hui，REN Xiao-ning，CHANG Hai

(Xi′an Modern Chemistry Research Institute, Xi′an 710065, China)

Abstract:The mathematical models and calculation methods for estimating the safe storage life, service life and reliable storage life of explosives and propellants and their products were reviewed, including commonly used Arrhenius equation, Berthelot equation and temperature coefficient equation, modified Arrhenius equation, accelerated factor equation, Eyring equation with multiple stress factors, cumulative damage model with alternating aging temperature, BP neural network method, structural life and reliable life prediction method etc. The simple and fast methods of point-slope method and single temperature timing method were proposed. It is considered that the reliability and reliable storage life of explosives and propellants and their products can be calculated by the so-called boundary model of the failure probability. Some computational methods were compared, and the conditions for estimating the same life by the Arrhenius equation and the Berthelot equation were given. The use scope of these methods or equations was pointed out, and some examples were given to illustrate the practical applications of some models and calculation methods. With 30 references.

Keywords:physical chemistry; explosive and propellant; life prediction; calculation method of life; safe life; service life; reliable storage life

中图分类号：TJ55；O64

文献标志码：A

文章编号：1007-7812(2016)02-0001-07

作者简介:刘子如(1940-) , 男, 研究员, 研究领域为火炸药热化学热分析。E-mail:lzr479@sina.com

基金项目:国家安全重大基础研究项目

收稿日期:2015-08-28；修回日期:2015-11-18

DOI：10.14077/j.issn.1007-7812.2016.02.001