快速r循环分块Jacket变换*

刘桂波，罗大庸，郭　迎

中南大学信息科学与工程学院，长沙410083

ISSN 1673-9418 CODEN JKYTA8

Journal of Frontiers of Computer Science and Technology

1673-9418/2016/10(04)-0582-07



快速r循环分块Jacket变换*

刘桂波+，罗大庸，郭迎

中南大学信息科学与工程学院，长沙410083

ISSN 1673-9418 CODEN JKYTA8

Journal of Frontiers of Computer Science and Technology

1673-9418/2016/10(04)-0582-07

E-mail: fcst@vip.163.com

http://www.ceaj.org

Tel: +86-10-89056056

* The National Natural Science Foundation of China under Grant Nos. 61379153, 61401519, Z201510120620003 (国家自然科学基金); the New Century Excellent Talent Foundation from MOE of China under Grant No. NCET-11-0510 (教育部新世纪优秀人才支持计划).

Received 2015-12,Accepted 2016-02.

CNKI网络优先出版: 2016-02-26, http://www.cnki.net/kcms/detail/11.5602.TP.20160226.0948.002.html

摘要：由中心权重哈达玛变换发展而来的Jacket变换，因其正交性、求逆简单和拥有快速算法等特点逐渐受book=583,ebook=137到关注。Jacket变换可应用于信号与图像处理、数字移动通信、量子编码、大数据处理等领域。为了进一步丰富Jacket变换理论，提出了一种通用的循环分块Jacket变换（r-circulant block Jacket transform，r-CBJT）。同时基于基本的r循环分块矩阵的性质，给出了任意阶r循环分块Jacket变换矩阵的构造方法。随后进一步推导了任意阶r循环分块Jacket变换矩阵的快速构造与分解算法，该快速算法可表示为单位矩阵与低阶Jacket矩阵连续克罗内克积的迭代形式。相比直接计算算法，该快速算法拥有更高的计算效率，且该快速算法也可应用于具有类似结构的其他类型的r循环分块Jacket变换。

关键词：哈达玛变换；r循环分块Jacket变换；克罗内克积；构造与分解；快速算法

1　引言

哈达玛变换、哈尔变换、离散傅里叶变换以及它们的变体都是离散正交变换，且已经广泛应用于信号与图像处理、移动通信等领域[1-4]。受中心权重哈达玛变换的启发而提出来的Jacket变换是一种特殊的变换[5]，其对应的逆变换矩阵可以由正向变换矩阵的元素或分块逆来获得[6]。Jacket变换也可应用于信号与数据处理[1]、数字无线通信[7]、加解密[8]、编码设计[9]等领域。同时，许多常见的矩阵，譬如哈达玛矩阵、离散傅里叶矩阵、斜矩阵、某些循环（分块）矩阵，都属于Jacket变换矩阵家族。除此之外，Jacket变换矩阵还与常用的酉矩阵、埃尔米特矩阵等有着密切的联系。

有关离散正交矩阵及其变换的文献主要涉及探索新的正交变换以及拓展各种变换的实际应用等方面。分块Jacket变换已应用于量子信号处理[10]、大数据处理[11]、新一代移动通信等。新的正交变换，诸如复哈达玛变换[12-14]、分式哈达玛或Jacket变换[15]、参数化变换[16-18]、混杂变换[7]、更一般的正交变换等[14]，逐渐被提出并不断地丰富着正交变换家族。

最近，出现了有关分块Jacket变换及其应用的文献。其中，文献[19]首次提出了快速可逆分块Jacket变换，且实现了N=2k或3k的一维和二维可逆分块Jacket变换矩阵的快速算法。随后，相关文献又提出了中心权重分块Jacket变换，且基于稀疏矩阵分解原理设计了该类Jacket变换矩阵的快速算法。此后，文献[6]基于量子信息系统里常见的泡利矩阵定义了一种通用的分块Jacket变换，同时给出了该类分块Jacket变换矩阵的快速构造和分解算法。但据了解，至今未有涉及循环分块Jacket变换理论及其应用的文献。

本文组织结构如下：第2章给出r循环分块Jacket变换矩阵的数学定义；第3章推导了任意阶r循环分块Jacket变换存在的条件，该条件间接地提供了构造相应变换矩阵的方法；第4章设计实现了r循环分块Jacket变换的快速构造与分解算法；相比直接计算算法，该快速算法的复杂度分析将在第5章详细给出；最后是全文的结论。

2　r-CBJT矩阵的结构

若分块矩阵[R]n=N/p（符号[∙]表示分块矩阵，下标代表单行或单列包含的子矩阵或子块矩阵的个数）拥有如下形式的结构，则称该类型矩阵是r循环分块矩阵：

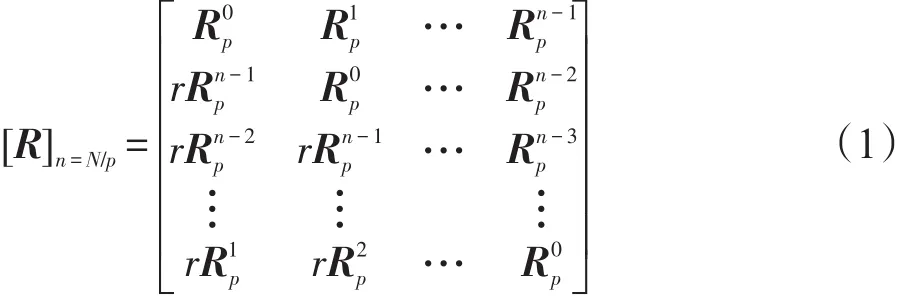
其中，Rin是序号为i∈(0, 1,…, n-1)且矩阵元素可为实数或复数的p×p的子矩阵，r为非零实数。如果p=1，则n×n维r循环分块矩阵是n×n维r循环矩阵。

同时，对于矩阵JN，定义其相关矩阵JRTN由原矩阵JN的元素交换行列下标并求倒数来获得。也即，矩阵JRTN的(k,i)位置的元素等于矩阵JN的(i, k)位置元素的倒数。

定义2（r-CBJT矩阵）若矩阵元素为p×p子矩阵的r循环分块矩阵[R]n=N/p是Jacket矩阵，则称矩阵[R]n=N/p是r循环分块Jacket矩阵。特别地，若p=1，则[R]n=N/p是r循环Jacket矩阵。

例1给定非零常量r，如下条件若成立：

则矩阵J2是r循环分块Jacket矩阵：

例2假定ω是单位1的复三次根，且如下等式成立：

则矩阵J3也是r循环分块Jacket矩阵：

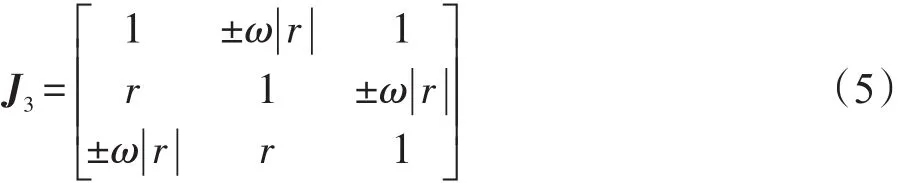
以上列举的两个r循环矩阵都是r-CBJT矩阵的特例。若r=1，则两个r循环Jacket矩阵为循环Jacket矩阵；若r=-1，则两个r循环Jacket矩阵即为反循环Jacket矩阵。

本章给出了r循环分块Jacket矩阵结构的数学描述，同时为了更清晰地描述，列举了几个例子。下文将推导r循环分块Jacket矩阵的一般存在性条件及其构造方法。

3　r-CBJT矩阵的构造方法

本章将结合基本r循环分块矩阵的性质与r-CBJT矩阵的特殊结构，推导任意阶r循环分块Jacket矩阵的一般性构造方法。

定理1假定n×n维矩阵具有如下形式：

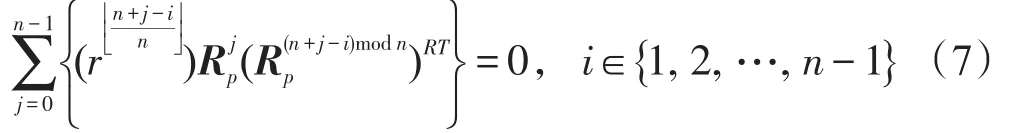
其中符号ëx û表示“向下取整”，或者说“向下舍入”，即取不大于x的最大整数。

证明假定一个基本的n×n维r循环矩阵表示为如下形式：

则有Πn=rIn和Π0=In。于是，[R]n[R]RTn可转换为：

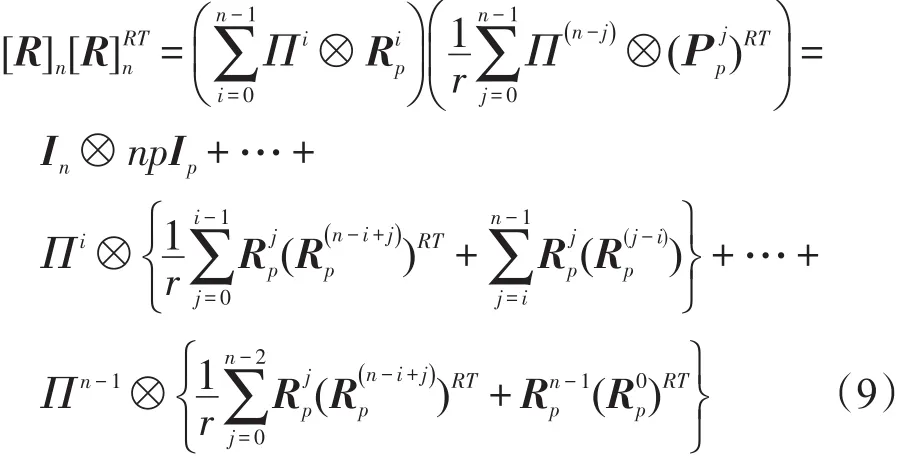
因此，若[R]n[R]RTn=In⊗npIp，当且仅当如下条件必须成立：

其中i∈{1, 2,…, n-1}。因此定理1得证。□

推论1假定2×2维r循环分块矩阵表示为如下形式：

其中，子矩阵都是Jacket矩阵，则该矩阵是Jacket矩阵，当且仅当如下等式成立：

证明根据式（7），令n=2，由式（13）可直接获得式（13）。因此推论1成立。□

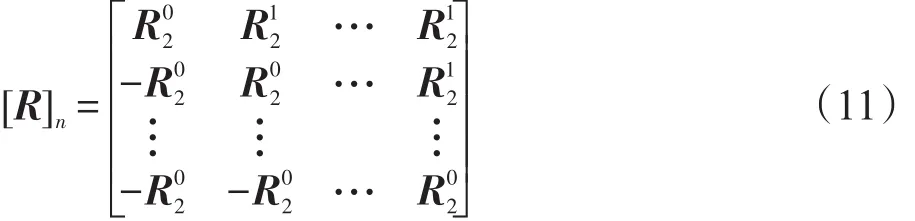
推论2假定n×n维的r循环分块矩阵表示为如下形式：

其中，所有子矩阵都是Jacket矩阵。r循环分块矩阵[R]n是r-CBJT矩阵，当且仅当如下等式成立：

证明根据式（7），易验证该推论也成立。□

该推论为任意阶r循环Jacket矩阵的构造提供了一种间接的方法。换而言之，已有的循环或反循环（分块）Jacket变换矩阵都可间接地基于式（7）来构建。也即，新提出的r-CBJT矩阵是一种通用的Jacket变换矩阵。另一方面，随着实际应用中Jacket变换矩阵的维数不断增加，如何快速地构造或分解相对高阶r-CBJT矩阵是一个值得研究的问题。

4　快速算法

基于定理1，可以构造任意相对高阶r-CBJT矩阵。该类矩阵可潜在应用于大数据处理、新一代移动通信等领域。研究相对高阶r-CBJT矩阵的快速算法具有理论和实际意义。

定理2假定n×n维r-CBJT矩阵表示为[R]n=qkpj，此处省略指示子矩阵维数的标号。矩阵[R]n=qkpj可按照如下方式快速构建：

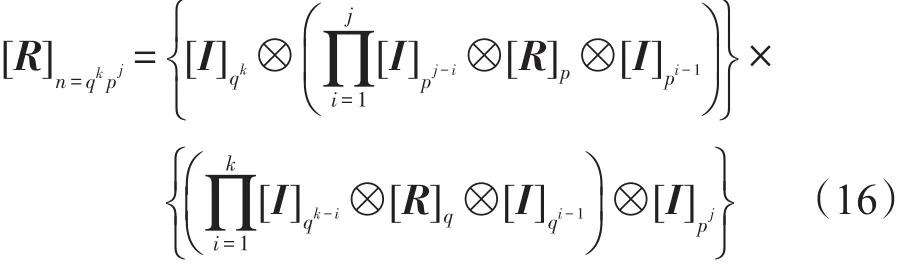
其中p和q互为素数。矩阵[R]p和[R]q可根据定理1来构造。

证明该定理的证明可以分两步。首先通过归纳法推导如下等式成立：

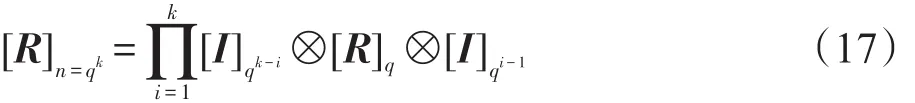
若k=1，式（17）可变换为：

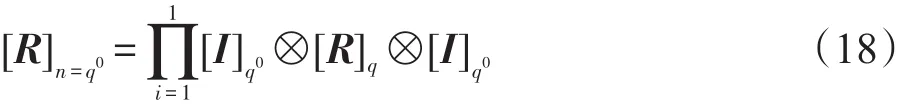
式（18）显然成立。若令k=L，式（17）成立，则可得如下等式：

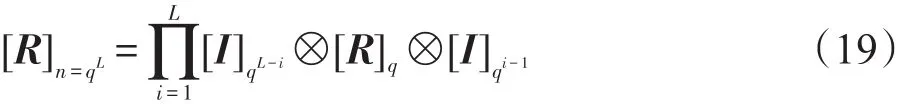
当k=L+1，利用克罗内克积的性质可得：

结合式（19）和（20），式（17）成立。同理可得：

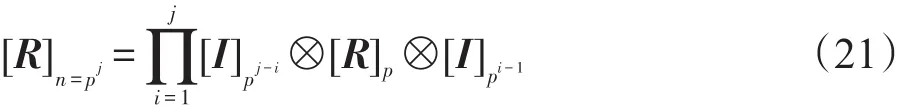
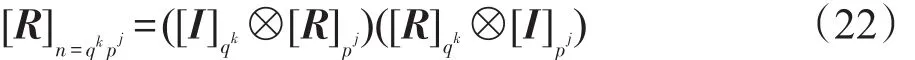
将式（20）和（21）代入式（22），定理2即可得证。□

该定理间接提供了快速构建r-CBJT矩阵的方法。譬如r-CBJT矩阵[R]n=72=([I]8⊗[R]9)([R]9⊗[I]8)，又[R]8=23

={[R]2⊗[I]2⊗[I]2}{[I]2⊗[R]2⊗[I]2}{[I]2⊗[I]2⊗[R]2}且[R]9=32={[R]3⊗[I]3}{[I]3⊗[R]3}。因此交替使用定理1和定理2，最终可获得矩阵[R]n=72的快速实现方法。

矩阵变换在实际应用中常会涉及前后向矩阵，譬如信号图像处理、编码设计、加解密、数字移动通信等。因此进一步研究r-CBJT矩阵的快速分解同样具有重要意义。

定理3假定r-CBJT矩阵[R]n=qkpj可分解为互为素数维数的Jacket矩阵[R]q和[R]p，则该矩阵可根据式（16）来快速分解。

证明因该过程是快速构造过程的逆过程，故定理3显然成立。□

例如，令r-CBJT矩阵[R]15的子矩阵是具体的数，而非矩阵，则其对应的分解过程可表示为：

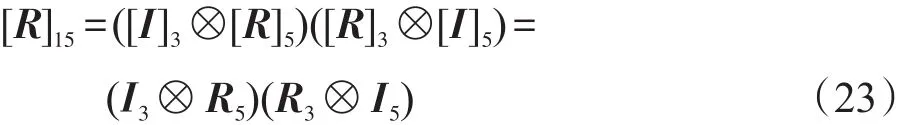
同时，其对应的信号流程图如图1所示。

Fig.1 Signal flow graph for fast decomposing a r-CBJM with size 15图1　15阶r循环Jacket矩阵的快速分解信号流程图

由图1可知，[R]15的分解包含两个步骤。其中，第一层包含5个相对独立的计算单元，而第二层有3个独立的计算单元。换而言之，快速分解过程得益于分解过程中出现的许多稀疏矩阵。为了后续研究查询的方便，表1梳理了20阶以内的r-CBJT矩阵的快速分解过程。其中第二列表示20以内整数的素数分解，第三列表示r-CBJT矩阵的快速分解算法。

Table 1 Fast decomposition approaches of r-CBJMs with size from 1 to 20表1　20阶以内r-CBJT矩阵的快速分解方法

5　复杂度比较分析

本章对r-CBJT变换的快速算法与直接计算算法进行了复杂度比较分析。对于任何N维r-CBJT矩阵，其直接计算算法和快速算法分别需要N(N-1)和kpk(p-1)次算术加法运算，同时分别需要N2和kpk(p-1)2次算术乘法运算。表2归纳总结了算法复杂度的一般性描述公式，其中FCA和DCA分别表示快速算法和直接计算算法。基于表2的结论，可以获得任意阶r-CBJT矩阵的两种算法所需要的计算支出。譬如，矩阵[R]27=33，直接计算算法分别需要702次和709次算术加法和乘法运算，而快速算法仅需162和108次算术加法和乘法运算。为了更直观地呈现，图2比较了20阶以内r-CBJT矩阵快速算法和直接计算算法分别需要的计算支出。

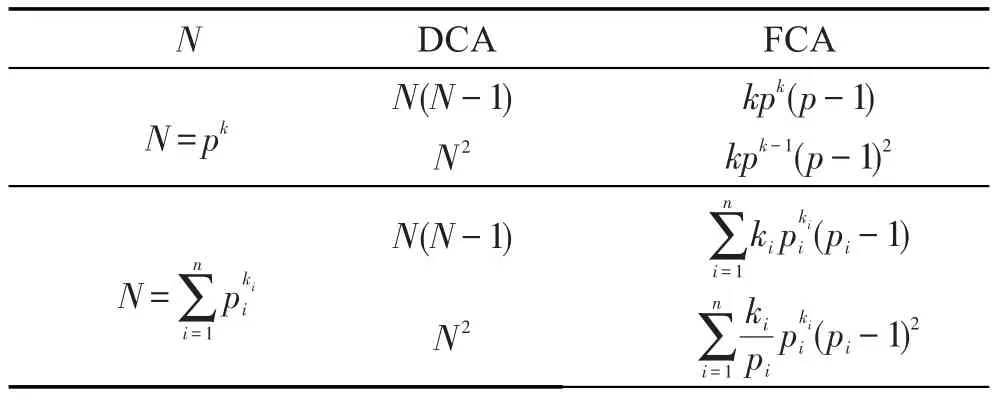
Table 2 Complexity comparison analysis between fast and direct calculation algorithms of r-CBJMs表2　r-CBJT矩阵的快速算法与直接计算算法复杂度比较分析

Fig.2 Complexity comparison analysis between fast and direct calculation algorithms of r-CBJMs with size from 2 to 20图2　2到20维r-CBJT矩阵FCA和DCA算法复杂度比较分析

很明显，直接计算算法的复杂度随着矩阵阶数的增加呈二次递增趋势。而快速算法随着矩阵阶数的增加上下波动。对于矩阵维数可以表示为互为素数积形式的r-CBJT矩阵，快速算法优势明显。

6　结束语

新定义的r循环分块Jacket矩阵拥有一般Jacket矩阵的良好结构与性质。由推导获得的r-CBJT矩阵一般性存在条件可以间接地构造出任意阶循环、反循环或r循环（分块）Jacket矩阵。基于稀疏矩阵分解的方法可以设计实现r-CBJT矩阵的快速构造和分解算法，该快速算法表现为单位矩阵与低阶（分块）Jacket矩阵连续克罗内克积的迭代形式。相比r-CBJT矩阵的直接计算算法，新提出的快速算法具有更低的计算复杂度，且该算法可以应用于其他类似拥有r-CBJT结构的Jacket矩阵的快速计算。其他类型的r-CBJT矩阵及其诸如此类矩阵的实际应用将在后续工作中开展。

References:

[1] Kyochi S, Tanaka Y. General factorization of conjugatesymmetric Hadamard transforms[J]. IEEE Transactions on Signal Processing, 2014, 62(13): 3379-3392.

[2] Liu Guibo, Huang Dazu, Luo Dayong, et al. Fast Jacket-Haar transform with any size[J]. Mathematical Problems in Engineering, 2015. doi:10.1155/2015/628642.

[3] Tao Ran, Li Yanlei, Wang Yue. Short-time fractional Fourier transform and its applications[J]. IEEE Transactions on Signal Processing, 2010, 58(5): 2568-2580.

[4] Ahmed N, Rao K R. Orthogonal transforms for digital signal processing[M]. New York: Springer, 1975.

[5] Lee M H. The center weighted Hadamard transform[J]. IEEE Transactions on Circuits and Systems, 1989, 36(9): 1247-1249.

[6] Zeng Guihua, Lee M H. A generalized reverse block Jacket transform[J]. IEEE Transactions on Circuits and Systems, 2008, 55(6): 1589-1600.

[7] Lee M H, Khan H A, Kim K J, et al. A fast hybrid Jacket-Hadamard matrix based diagonal block-wise transform[J]. Signal Processing Image Communication, 2014, 29(1): 49-65.

[8] Aung A, Ng B P, Rahardja S. A robust watermarking scheme using sequency-ordered complex Hadamard transform[J]. Journal of Signal Processing Systems, 2011, 64(3): 319-333.

[9] Song Wei, Lee M H, Matalgah M M, et al. Quasi-orthogonal space-time block codes designs based on Jacket transform[J]. Journal of Communications and Networks, 2010, 12(3):240-245.

[10] Shi Ronghua, Guo Ying, Lee M H. Quantum codes based on fast pauli block transforms in the finite field[J]. Quantum Information Processing, 2010, 9(5): 611-628.

[11] Li Jun, Yan Yier, Duan Wei, et al. Tensor decomposition of Toeplitz Jacket matrices for big data processing[C]//Proceedings of the 2015 International Conference on Big Data and Smart Computing, Jeju, Korea, Feb 9-11, 2015. Piscataway, USA: IEEE, 2015: 11-14.

[12] Aung A, Ng B P, Rahardja S. Sequency-ordered complex Hadamard transform: properties, computational complexity and applications[J]. IEEETransactions on Signal Processing, 2008, 56(8): 3562-3571.

[13]Wu Jiasong, Wang Lu, Yang Guanyu, et al. Sliding conjugate symmetric sequency-ordered complex Hadamard transform: fast algorithm and applications[J]. IEEE Transactions on Circuits and Systems, 2012, 59(6): 1321-1334.

[14] Pei S C, Wen C C, Ding J J. Sequency-ordered generalized Walsh-Fourier transform[J]. Signal Processing, 2013, 93(4): 828-841.

[15] Mao Yun, Peng Jun, Guo Ying, et al. On the fast fractional Jacket transform[J]. IEEE Transactions on Circuits Systems and Signal Processing, 2014, 33(5): 1491-1505.

[16] Bouguezel S, Ahmad M O, Swamy M N S. A new class of reciprocal-orthogonal parametric transforms[J]. IEEE Transactions on Circuits and Systems, 2009, 56(4): 795-805.

[17] Bouguezel S, Ahmad M O, Swamy M N S. New parametric discrete Fourier and hartley transforms, and algorithms for fast computation[J]. IEEE Transactions on Circuits and Systems, 2011, 58(3): 562-575.

[18] Lee M H, Zhang Xiaodong, Jiang Xueqin. Fast parametric reciprocal-orthogonal Jacket transforms[J]. EURASIP Journal on Advances in Signal Processing, 2014. doi: 10.1186/ 1687-6180-2014-149.

[19] Lee M H, Hou Jia. Fast block inverse Jacket transform[J]. IEEE Signal Processing Letters, 2006, 13(8): 461-464.

LIU Guibo was born in 1981. He is a Ph.D. candidate at Central South University. His research interests include orthogonal transforms and signal and image processing, etc.

刘桂波（1981—），男，湖南邵阳人，中南大学信息科学与工程学院博士研究生，主要研究领域为正交变换，信号与图像处理等。

LUO Dayong was born in 1944. He is a Ph.D. supervisor at Central South University. His research interests include signal and image processing, control theories and application, etc.

罗大庸（1944—），男，湖南长沙人，中南大学信息科学与工程学院博士生导师，主要研究领域为信号与图像处理，控制理论与应用等。发表学术论文70多篇，其中SCI检索20余篇。

GUO Ying was born in 1975. He received the Ph.D. degree in electronic engineering from Shanghai Jiao Tong University in 2006. Now he is a Ph.D. supervisor at Central South University. His research interests include quantum communication and network security, etc.

郭迎（1975—），男，山东曲阜人，2006年于上海交通大学电子工程学院获得博士学位，现为中南大学信息科学与工程学院博士生导师，主要研究领域为量子通信，网络安全等。发表学术论文100多篇，其中SCI检索70余篇，EI检索30余篇。

Fast r-Circulant Block Jacket Transformƽ

LIU Guibo+, LUO Dayong, GUO Ying
School of Information Science and Engineering, Central South University, Changsha 410083, China

+ Corresponding author: E-mail: lgbtrs2006@126.com

LIU Guibo, LUO Dayong, GUO Ying. Fast r-circulant block Jacket transform. Journal of Frontiers of Computer Science and Technology, 2016, 10(4)：582-588.

Abstract:Jacket transform, inspired by the well-known Hadamard transform, has been attracting more and more attentions due to its orthogonality, simplicity of matrix inversion and existence of fast algorithm. Jacket transform is applied to signal and image processing, digital mobile communication, quantum coding and big-data processing, etc. To further enrich the theory of Jacket transform, this paper proposes a generalized r-circulant block Jacket transform (r-CBJT). Meanwhile, this paper suggests an approach for the elegant construction of the r-circulant block Jacket matrices (r-CBJMs) with any size by using the structure of the permutation matrices. After that, fast construction and decomposition algorithms of r-CBJMs are designed with the Kronecker product of corresponding identity matrices and relative lower order Jacket matrices in a successively iterative form. They have less computation complexity compared to direct calculation approach. Furthermore, the proposed approach can be employed to other r-CBJTs with similar characteristics.

Key words:Hadamard transform; r-circulant block Jacket transform; Kronecker product; construction and decomposition; fast algorithm

文献标志码：A

中图分类号：TP301

doi:10.3778/j.issn.1673-9418.1601008