矩阵求逆应用于等离子体杂质体发射率测量的研究

沈永才，程　飞，吴义恒

(安庆师范学院 物理与电气工程学院，安徽 安庆 246133)



矩阵求逆应用于等离子体杂质体发射率测量的研究

沈永才，程飞，吴义恒

(安庆师范学院 物理与电气工程学院，安徽 安庆 246133)

摘要：对托卡马克等离子体中获得杂质局部体发射率的过程进行研究，提出了一种采用求逆矩阵的方法进行Abel反演，根据弦积分的杂质光亮度分布获得杂质局部体发射率。结合托卡马克装置假象的钼杂质弦积分剖面，采用该方法获得了杂质的体发射率分布。

关键词：逆矩阵；Abel反演；杂质体发射率

杂质总是不可避免的存在于托卡马克等离子体中，主要来源于等离子体与第一壁、限制器、偏滤器等的相互作用。杂质对高温等离子体具有重要的影响，主要体现在[1,2]：第一，杂质辐射(轫致辐射、复合辐射和线辐射)会带走大量能量，降低能量约束时间并导致等离子体由高约束模式向低约束模式转变；第二，杂质的存在会降低主粒子的比重，降低主等离子体的含量，从而降低聚变反应功率密度。对杂质行为和其输运研究一直是托卡马克等离子体物理研究的重要课题之一。要了解杂质行为和输运对等离子体约束的影响，首先需要知道杂质在等离子体中的含量。

对于一个内部比较复杂且不容易侵入的系统，它的内部信息很难测量，尤其是局域信息，有时候需要通过反演来获得。利用托卡马克等离子体光谱诊断进行杂质线辐射测量时，探测的结果大多是弦积分值。这时要获得杂质密度的空间分布就需要通过反演算法获得局部的体发射率。但高温等离子体存在不可接近性，且诊断系统观测弦一般是单阵列的，这给空间反演带来很大的困难。通常会假定物理量在磁面上是中心对称或轴对称分布，将物理量反演到磁面上，这种假设下可以采用Abel变换进行反演计算。在高温等离子体光谱诊断中，大部分的弦积分量是非平行的。一般将托卡马克磁面分为圆对称和非圆对称(偏滤器位形)。对于圆对称截面，Abel变换常用的方法有Bockasten法、三次样条函数法、Barr法等；而对于非圆对称的，Abel变换常用的方法有切片法和分离变量法，但这些方法都非常复杂。本文以东方超环(Experimental Advanced Superconductor Tokamak，EAST)装置上的软X射线及极紫外光谱诊断测量的杂质弦积分为例，介绍一种采用逆矩阵变换进行Abel反演来求解杂质体发射率的方法，主要应用于托卡马克等离子体杂质密度的计算。

1逆矩阵法进行Abel变换反演

由光学诊断系统观测到的杂质线辐射谱线为弦积分量，在系统完成绝对标定的情况下，经过标定系数转换可以获得光亮度(弦积分量)。光亮度和局部体发射率存在一定的数学关系，可以用下式表示[3]：

(1)

其中，B为测量的光亮度(弦积分量)，i为观测弦道数编号，E为体发射系数(局域量)，一般认为体发射系数在固定的磁面内是定值，而磁面只与径向距离r相关。由阿贝尔变换可得[4]：

(2)

将等离子体磁面进行分区处理，(2)式中的j即为分区编号，具体求解时，可采用离散化处理，则B和E的关系可以写成：

(3)

在已知光亮度B的情况下，需要求的量为体发射系数E，可以采用矩阵求逆，将(3)式变为

(4)

1.1圆截面位形Abel反演(限制器位形)

(5)

图1　圆截面位形Abel反演示意图

1.2非圆截面位形Abel反演(偏滤器位形)

一般情况下，EAST(EAST小半径为0.45 m，拉长比通常在1.7左右)装置放电位形为偏滤器拉长位形，即非圆截面位形。图2显示了XEUV[4-6]在EFIT磁面上的光路图。XEUV观测的范围为0～450 mm(磁轴往上)，可包含21条弦(实线标记为实际测量弦)，而离磁轴450 mm以上的假想弦(虚线标记)。图中的EAST等离子体放电位形为类椭圆形，每个圆的半径都不固定，则长度矩阵Lij不能用圆位形情形下的方法来求。这里将长度矩阵区域划分为强磁场区和弱磁场区长度矩阵。磁面信息可以从EAST EFIT上读取，将磁面进行区域划分，选出与观测弦相切的磁面。依次找出每一条弦和其非相切圆相交的交点，见图3所示。用i，i+1和i+2等表示观测弦，用j，j+1和j+2等表示相切圆。利用(x,y)坐标表示每个交点的位置，则长度矩阵可以用两点间距离及距离差来表示，即

(6)

图2　EUV光谱仪在EAST磁面上的光路图

图3　非圆截面Abel反演示意图

2Abel反演获得杂质体发射率实例

采用第1部分介绍的方法，可以对假象的杂质体发射率进行反演计算。如假定实验中XEUV测量到的Mo杂质线辐射弦积分剖面如图4所示，在系统完成绝对标定之后，通过该方法反演计算得到的体发射率系数如图5所示。

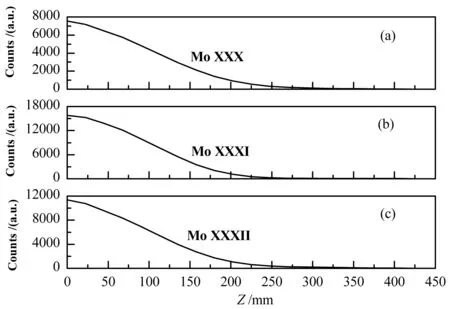
图4　EAST装置假想的钼杂质线辐射剖面

图5　EAST装置H-模放电的钼杂质体发射率剖面

3结束语

Abel反演对于托卡马克等离子体中杂质辐射测量来说，具有重要的意义。本文所提出的采用逆矩阵求解法反演获得杂质体发射率分布的方法相比其他方法，具有思路简单、易于计算的特点。基于等磁通面的方法，克服了非圆截面观测弦非对称性的缺点，巧妙利用数学量以及物理量之间的关系。只要物理量通过等离子体平衡反演得到等离子体磁面分布，就可在此基础上进行相关物理量的反演计算。

参考文献:

[1]Z.Y.Cui,S.Morita,B.Z.Fu,etal..Space-resolvedvacuumultravioletspectrometersystemforedgeimpurityandtemperatureprofilemeasurementinHL-2A[J].ReviewofScientificInstruments, 2010, 81: 1-8.

[2]Z.Y.Cui,Q.M.Wang,J.F.Dong,etal..ImpuritymeasuredbyVUVspectrometerandOMAonHL-2Atokamak[J].PlasmaScience&Technology, 2004, 6: 2359-2363.

[3] 沈永才.EAST软X射线及极紫外光谱诊断系统的研制与杂质输运研究[D].合肥: 中国科学院大学，2014.

[4]Y.C.Shen,X.W.Du,W.Zhang,etal..Space-resolvedextremeultravioletspectrometersystemforimpuritybehaviorresearchonexperimentaladvancedsuperconductingtokamak[J].NuclearInstrumentsandMethodsinPhysicsResearchSectionA, 2013, 700(1): 86-90.

[5]Y.C.Shen,B.Lu,X.W.Du,etal..Spatially-resolvedflat-fieldsoftx-rayspectrometeronexperimentaladvancedsuperconductingtokamak[J].FusionEngineeringandDesign, 2013, 88(11):3072-3077.

[6]Y.C.Shen,B.Lyu,X.W.Du,etal..Impurityemissionbehaviorinthesoftx-rayandextremeultravioletrangeonEAST[J].PlasmaScienceandTechnology, 2015, 17(3):183-187.

Obtaining of Tokamak Plasma Impurities Emissivities Profiles by Using Matrix Inversion Method

SHEN Yong-cai, CHENG Fei, WU Yi-heng

(School of Physics and Electrical Engineering， Anqing Teachers College, Anqing, Anhui 246133, China)

Abstract:In this paper，process of obtaining impurity emissivity on tokamak plasma has been studied. By using matrix inversion, emissivity can be calculated according to brightness of impurity spectral lines. As an example， Mo emissivities have been calculated by using this method based on the assumed brightness.

Key words:matrix inversion, Abel inversion, impurity emissivity

文章编号：1007-4260(2016)01-0076-03

中图分类号：TL65.1

文献标识码：A

DOI：10.13757/j.cnki.cn34-1150/n.2016.01.020

作者简介：沈永才，男，安徽安庆人，博士，安庆师范学院物理与电气工程学院讲师，研究方向为等离子体物理。E-mail:syc1015@Sina.com

基金项目：安徽省教育厅高校自然科学研究重点项目(KJ2016A434)和安庆师范学院博士启动专项基金(044-140001000024)。

*收稿日期：2015-12-30

网络出版时间：2016-03-15 17:05网络出版地址：http://www.cnki.net/kcms/detail/34.1150.N.20160315.1705.020.html