三种处理含理想电源复杂电路的方法及比较

张 平 伟

(安庆师范学院 物理与电气工程学院，安徽 安庆 246133)



三种处理含理想电源复杂电路的方法及比较

张 平 伟

(安庆师范学院 物理与电气工程学院，安徽 安庆 246133)

摘要：以一个含有理想电源的复杂电路为例，讨论了支路电流法、结点分析法和回路分析法在分析含有理想电源复杂电路的解题方法及技巧。

关键词：理想电源；支路电流法；结点分析法；回路分析法

稳恒电源分为电压源和电流源，其中理想电压源和理想电流源是两种特殊情况。在一个回路中，理想电压源输出电压恒定，电路中端口电流随外电路负载变化而变化；而理想电流源输出电流恒定，电路中端口电压随外电路负载变化而变化[1-3]。由于理想电源中不含有电阻，在解决实际电路问题时，如何列出电源的端电压及流过它的电流之间关系式将变得非常棘手。支路电流法、结点分析法和回路分析法是求解复杂电路常用的3种方法，它们都是以基尔霍夫定律(包含关于结点电流的KCL方程、关于回路电压的KVL方程)为基础而展开。本文以应用这3种方法为主线，探讨电路中含有理想电源时的处理方法及技巧。

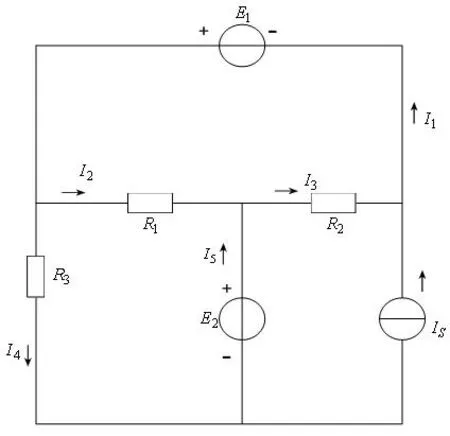
图1　含理想电源的复杂电路

如图1，设E1=4V，E2=16V，IS=3A，

R1=R2=R3=1Ω，各支路电流的参考方向如图所示，求各支路电流值大小。电路中含有理想电流源IS，理想电压源E1，E2。

1应用支路电流法求解

支路电流法是求解复杂电路的最基本方法，设电路中的结点数为n，支路数为p。在求解时一般步骤[1]：先标出各支路电流的参考方向，根据电流参考方向列出n-1个KCL方程，然后再列出p-(n-1)个KVL方程(一般等于网孔个数)，联立此p个方程即可求解各支路电流。在一般情形下，电路中有多少条支路，对应就有多少个未知数，应该列出多少个方程，即p个方程。

分析在本题中，共含有6条支路，4个结点，3个网孔，理论上需要6个方程才能求解出所有支路上的电流，但由于含有理想电流源IS，其所在支路的电流大小始终等于电流源的电流大小，即相当于有一个是已知量，可少列一个方程式，选择去掉包含理想电流源网孔的KVL方程式将使计算变的较为简单。

各支路电流的参考方向如图2所示，对结点A，B，C可列如下KCL方程：

I1-I2-I4=0

(1)

I2-I3+I5=0

(2)

IS+I3-I1=0

(3)

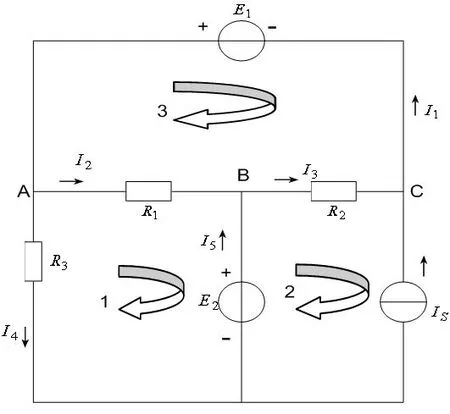
图2　应用支路电流法求解时电路图

选择网孔1，3列KVL方程：

I4R3-I2R1-E2=0

(4)

I2R1+I3R2-E1=0

(5)

将E1,E2,IS,R1,R2,R3带入(1)～(5)式，解得

I1=10A，I2=-3A，I3=7A，I4=13A，I5=10A，其中I2结果是负值，表明实际电流方向与图中参考方向相反。

从上面解题过程可以看出，支路电流法求解思路简单，一般复杂电路均可以采用此法求解，但是解题中所列方程式个数与支路的条数相同，所以在更为复杂的电路中涉及方程式过多，未知数也过多，使得求解变得困难，结点分析法与回路分析法相当于是此方法的简化。

2应用结点分析法求解

结点分析法一般步骤[1]：先标出各支路电流的参考方向，列出n-1个KCL方程；然后选择其中一个结点作为参考结点(电位为零)，标出其他独立结点相对于参考结点的电位(称为结点电压)，将支路电流表示成结点电压的函数；最后将此函数带入n-1个KCL方程中，即可求解。

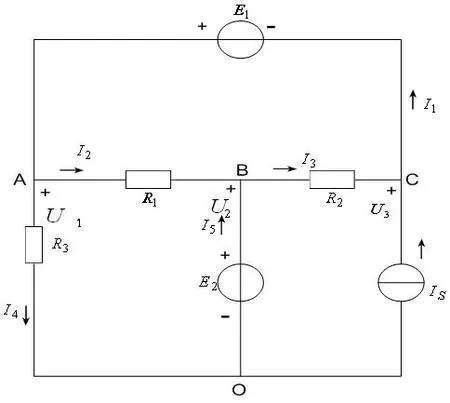
图3　应用结点分析法求解时电路图

从步骤中可以看出，一般情况下结点分析法只给出n-1个未知数，故只需n-1个方程式，相对于支路电流法是一种简化方法。

分析各支路电流的参考方向如图3所示，对结点A，B，C可列KCL方程，方程为上面的(1)～(3)式。取O点作为参考结点，结点A，B，C相对于O点的结点电压分别为U1，U2,U3，在本题中，电路中含有理想电压源E1,E2，它们对应所在的支路不含电阻，故对应的支路电流I1,I5不能表示成电压的函数，而I2,I3,I4可分别表示为

(7)

(8)

(9)

将(7)～(9)式代入(1)～(3)式得

(10)

(11)

(12)

(10)～(12)式由于未知，故不能解出U1，U2,U3，从数学角度上少了两个方程。但此时可利用理想电压源特性，其输出电压恒定，得如下两方程

U1-U3=E1

(13)

U2-0=E2

(14)

结合(10)～(14)式可解得

U1=13V,U2=16V,U3=9V

(15)

将(15)式代入(7)～(9)式可得：I2=-3A，

I3=7A，I4=13A，再将此结果代入(1)，(2)式中可解得：I1=10A，I5=10A。

3应用回路分析法求解

回路分析法一般步骤[1]：先标出各回路元件上电压的参考极性及回路路径绕行方向，列出网孔的KVL方程；然后规定各支路电流及回路电流的参考方向，列出支路电流与回路电流的关系式；再将元件上电压表示为回路电流的函数，代入网孔的KVL方程中，即可求解。

从步骤中可以看出，一般情况下回路分析法只给出网孔的未知数，故只需列出网孔的方程式，相对于支路电流法也是一种简化方法。

但该方法在将元件上电压表示为回路电流的函数时，若某条支路出现理想电流源，由于该支路不含电阻，此时不能将电压表示成电流的函数。出现这种情况时，可以将理想电流源所在回路的回路电流直接用理想电流源表示，相当于少一个未知数，可少列一个方程式，该方程式一般选择理想电流源所在网孔方程式。

分析各支路电流的参考方向如图4所示，设回路1的回路电流为IⅠ，回路2中因含有理想电流源IS，故回路电流直接设为IS，回路3的回路电流为IⅡ，回路电流方向与路径方向相同。根据解题步骤所述，这里共有两个未知数，故需两个KVL方程：

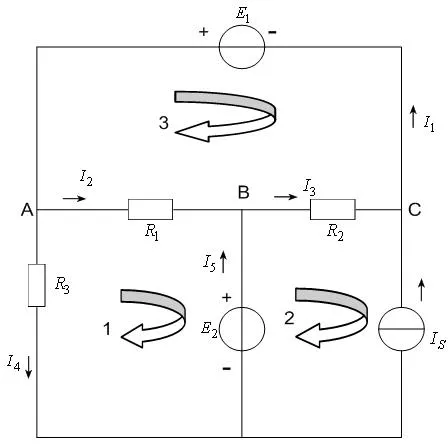
图4　应用回路分析法求解时电路图

解得IⅠ=-13A,IⅡ=-10A，从图中可以看出，

I1=-IⅡ=10A,I2=IⅠ-IⅡ=-3A,

I3=-IS-IⅡ=7A,I4=-IⅠ=13A,

I5=IS-IⅠ=10A。

4结束语

综上所述，在求解实际含有理想电源的复杂电路时，应用支路电流法求解，应将理想电流源所在的支路电流视为理想电流源的自身电流值，理想电压源只需考虑其电压即可；应用结点分析法求解时，理想电流源所在支路电流仍为理想电流源的自身电流值，而理想电压源所在支路则用连接理想电压源的两个结点电压相减等于理想电压源的电压值来代替缺少的方程；应用回路分析法求解时，含有理想电流源所在回路的回路电流直接用理想电流源表示，理想电压源只需考虑其电压即可。从求解过程来看，3种方法对于一般复杂电路都可以求解，但需要列的方程式个数不相同。支路电流法是最基础的方法，需要方程式最多，结点分析法、回路分析法可视为支路电流法的简化计算，当电路中网孔个数多于结点个数时，采用结点分析法，反之采用回路分析法。

参考文献:

[1] 郭木森.电工学[M].3版.北京：高等教育出版社，2011.

[2] 秦曾煌.电工学[M].7版.北京：高等教育出版社，2010.

[3] 唐介.电工学[M].2版.北京：高等教育出版社，2010.

Comparing Three Methods to Discuss Complex Circuit Including the Ideal Power Supply

ZHANG Ping-wei

(College of Physics and Electric Engineering，Anqing Teachers College，Anqing，Anhui 246133，China)

Abstract:Taking a complex circuit which includes the ideal power supply as an example, we discuss the problem-solving skills in the branch current method, the nodal analysis method and the loop analysis method.

Key words:the ideal power supply，branch current method，nodal analysis method，loop analysis method

文章编号：1007-4260(2016)01-0131-03

中图分类号：TM131.3

文献标识码：A

DOI：10.13757/j.cnki.cn34-1150/n.2016.01.033

作者简介：张平伟，男，安徽东至人，硕士，安庆师范学院物理与电气工程学院讲师，主要从事非成性动力学研究。E-mail: zhangpw@aqtc.edu.cn

*收稿日期：2014-05-11

网络出版时间：2016-03-15 17:05网络出版地址：http://www.cnki.net/kcms/detail/34.1150.N.20160315.1705.033.html