可压缩欧拉方程在不变子空间中的精确解∗

朱春蓉,朱丹霞

(安徽师范大学数学计算机科学学院，芜湖 241000)

1 引言

考虑n-维可压缩欧拉方程[1]

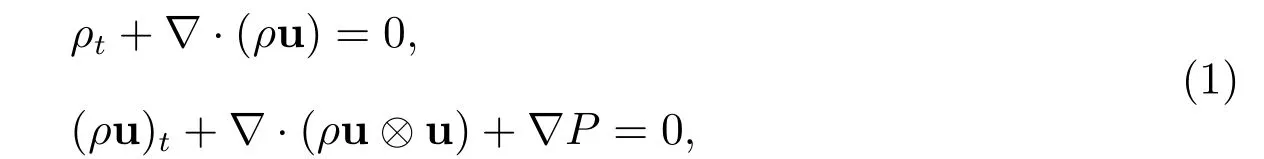
其中ρ=ρ(t,x)表示气体的密度，u=u(t,x)表示气体的速度，x∈Rn为空间变量，P=ργ/γ(γ≥1)表示压强，记号⊗表示张量积．

由于可压缩欧拉方程在物理学中的重要性和数学中带给人们的挑战性，使得人们对它越来越感兴趣(参考文献[2]及其参引文献)．在欧拉方程解的研究中，因为它的非线性性，人们很难给出它一般解的表达式．但通过拟设法，人们可以构造它的一些形式解并用于研究它的一些特殊性质．Liu在文献[3]中将速度的形式拟设为c(t)x，并代入带有阻尼项欧拉方程中研究其奇异性．随后在文献[4]中，作者研究了用于描述多方气体的n-维欧拉方程类似形式径向对称解的奇异性．在文献[5]中，Yuen将速度形式进行了扰动，即考虑速度形式为c(t)x+b(t)的解，并研究了一维欧拉方程的爆破性．Huang和Wang[6]应用李雅普诺夫方法和扰动方法，分析关于Chaplygin气体这种形式解的爆破性．上述文献都表明了一些特殊形式的解在研究这类方程性质中的重要性．在本文中，我们将应用不变子空间方法构造方程组(1)的精确解．不变子空间方法是一种纯数学的方法，并且较拟设方法更具数学依据．本文证明了，通过拟设法在文献[4,5]中得到的形式解都属于和欧拉方程相关的向量微分算子允许的函数空间．在变量变换意义下，通过不变子空间方法，方程组(1)被约化为一阶有限维动力系统．不同于上述参考文献中的研究，这种动力系统便于直接求解．由此，我们给出方程组(1)一些解的具体表达式．

本文将做如下安排：在第2节中，对应用于构造非线性演化方程组精确解的不变子空间方法进行简单介绍；在第3节中，给出与方程组(1)相关的向量微分算子允许的不变子空间，并将方程组(1)约化为有限维动力系统；在第4节中，通过例子的形式给出方程组(1)一些解的具体表达式．

2 不变子空间方法

不变子空间方法是一种与对称群方法相关的方法．通过这种方法，非线性演化方程可以被约化为有限维动力系统．早在文献[7]中，Galaktionov就用这种方法考虑了二次非线性微分算子的不变子空间，并用于构造大量的演化方程的精确解．后来，Galaktionov和Svirshchevskii将他们关于不变子空间方法的研究整理在文献[8]中．事实上，在变量变换的意义下，热方程的基本解就属于和其相关微分算子允许的函数空间．他们还利用不变子空间方法得到了渗流方程的精确解，这些精确解可以用于构造一些这种形式方程的弱解和爆破解，并利用比较原理研究它们一般解的性质[9,10]．近期，这种方法得到了一些新的进展和应用，可参考文献[11—16]．为了获得非线性演化方程组的解，Galaktionov和Svirshchevskii引进了向量集作为线性子空间的推广，在这些向量集中，每个向量的分量都属于同一个函数空间．在文献[11]中，Qu和Zhu将这种向量集进行了推广，给出了向量微分算子允许的不变子空间的定义，在这种不变子空间中每个向量的分量可以属于不同的函数空间，并在文献[12]中给出了这种不变子空间的维数估计．在本文中，我们将使用Qu和Zhu的方法构造方程组(1)的精确解．本节余下内容是关于这种方法的简介．

假设

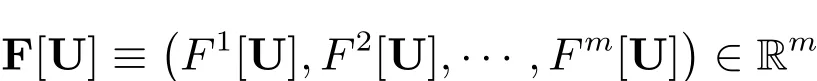
是一个向量微分算子，其中

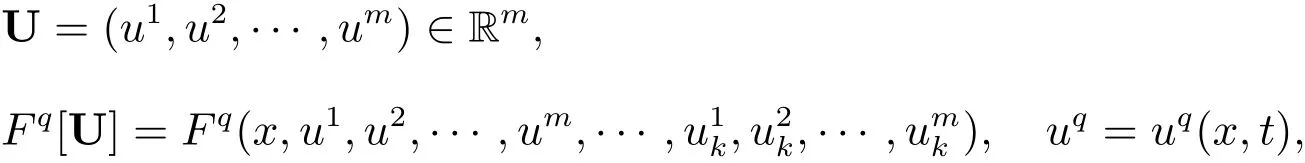
Fq(·)(q=1,2,···,m)是给定的光滑函数．我们将使用下面的记号

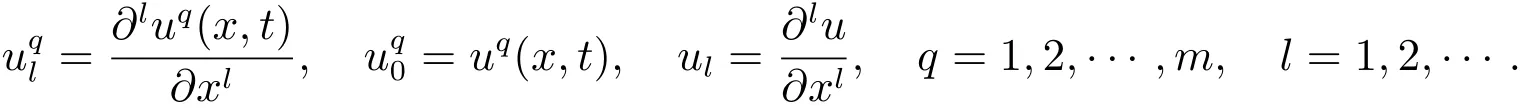
设W表示一个线性空间，其中

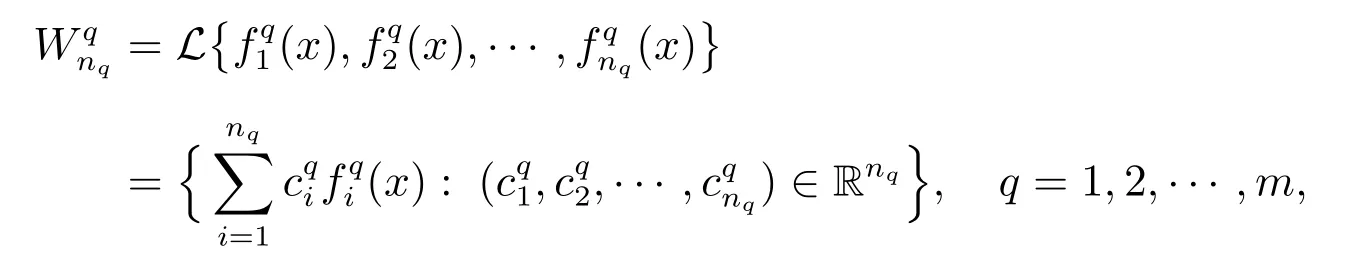
且(nq≥2)是相互线性无关的．如果向量微分算子F满足条件

即

则称向量微分算子F允许子空间W，这表明存在函数，使得

如果子空间W是被向量微分算子F[U]允许的，则相应的演化方程组Ut=F[U](或Utt=F[U])有解形如

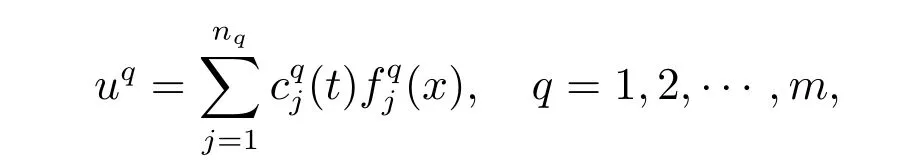
其中满足常微分方程组

假设是由下面的nq阶线性常微分方程

解空间定义的，则子空间W在算子F下不变的条件是

其中[Hq]表示方程Lq[uq]=0及其关于x的微分结果．

通过上述关于不变子空间方法的介绍，下面我们将使用它构造方程组(1)的精确解．

3 方程组(1)的不变子空间和约化

在本节，我们将给出和方程组(1)相关的向量微分算子允许的不变子空间，并将方程组(1)约化为有限维动力系统．

首先，我们考虑一维情形的欧拉方程组

其中P=ργ/γ(γ≥1)．当γ=1时，通过变量变换v=lnρ，方程组(4)可以转化为

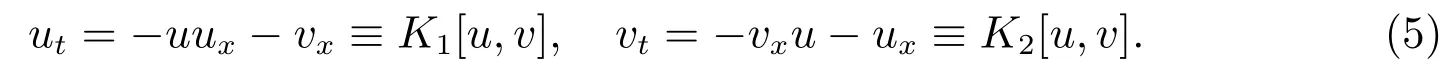
当γ＞1时，通过变量变换v=ργ−1/(γ−1)，方程(4)可以转化为

记

由参考文献[12]中的维数估计定理，我们考虑向量微分算子K和¯K允许的由(2)式定义的不变子空间时，要考虑下列情形

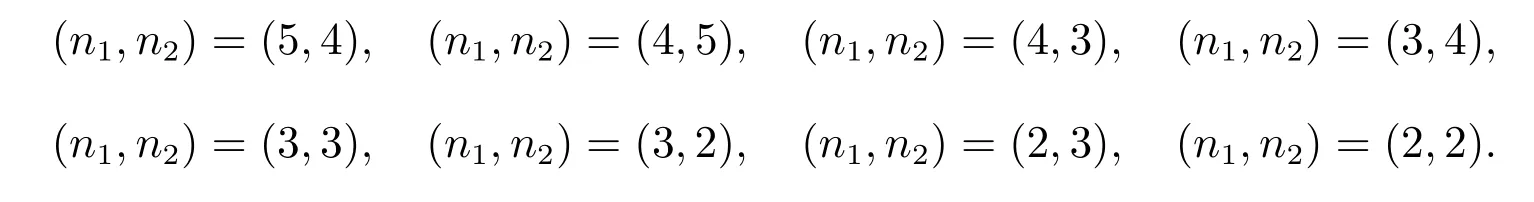
由不变条件(3)，我们得到下面的结果．

定理1向量微分算子K[u,v]和都只允许不变子空间=，其中

证明 假设K允许不变子空间，其中是由下列常微分方程的解空间定义的

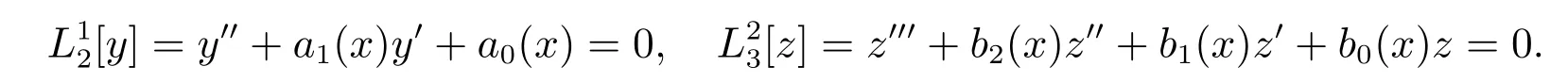
在这种情形下，不变条件(3)为

G1和G2均是ui,vj(i=0,1,j=0,1,2)的多项式，其中

考虑G1中各项的系数，我们得到

在这种情形下G2=0也是成立的．因此，向量微分算子K允许不变子空间×，其中=L{1,x}是由常微分方程y′′=0定义的，=L{1,x,x2}是由常微分方程z′′′=0定义的．通过类似的计算，我们还可以证明向量微分算子K允许子空间~W，并且还可以证明它不允许其它形式的由方程组(2)定义的不变子空间．上述结果对于向量微分算子也成立．

显然，．在不变子空间中，方程组(5)和(6)可分别被约化为如下的有限维动力系统

和

其次，我们考虑n-维欧拉方程(1)的球对称解．在欧拉方程(1)中，令ρ=ρ(x,t),u，则它们满足

其中x=|x|．类似地，当γ=1时，令v=lnρ，则方程组(9)被转化为

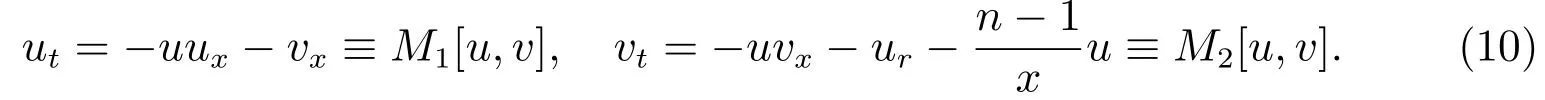
对于γ＞1，令v=ργ−1/γ，则方程组(9)被转化为

类似于定理1证明中的计算，我们可以证明没有由方程组(2)定义的线性子空间在向量微分算子M≡(M1[u,v],M2[u,v])和作用下不变．事实上，我们注意到

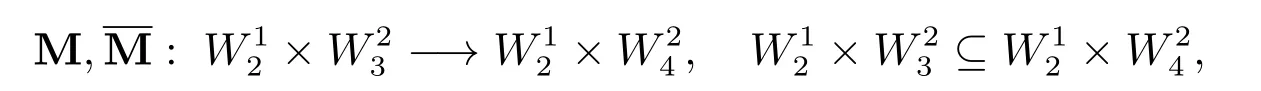
其中=L{1/x,1,x,x2}．在这种情形下，我们称线性子空间在向量微分算子M和M作用下部分不变．因此，我们可以构造方程组(10)和(11)如下形式的解

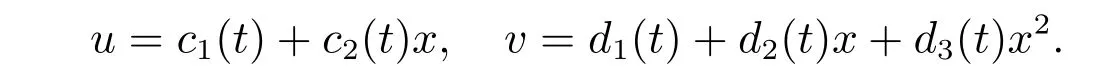
对于方程组(10)，ci(t)和dj(t)满足如下的约束条件

对于方程组(11)，ci(t)和dj(t)满足

4 欧拉方程的精确解

在第3节中，欧拉方程在变量变换的意义下，被约化为有限维动力系统．由于这些动力系统均是非线性的，很难给出它们的通解，但是我们可以通过计算给出它们一些具体的特解．在下文中，我们将用例子的形式给出这些特解．

例1在方程组(7)和(8)中，取d3(t)=0．此时，可以给出1-维欧拉方程(4)如下的解：

当γ=1时

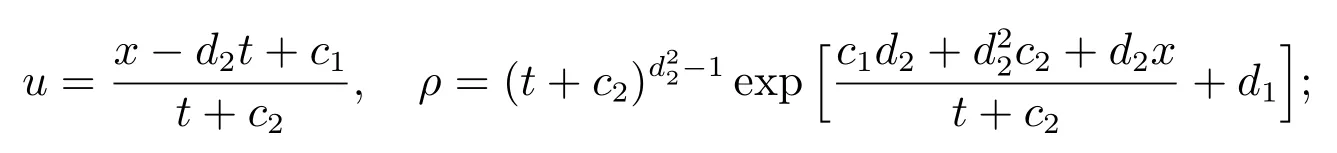
当γ=2时

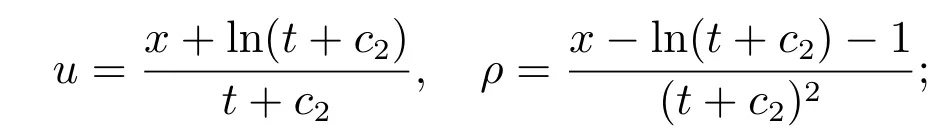
当γ＞1,γ/=2时

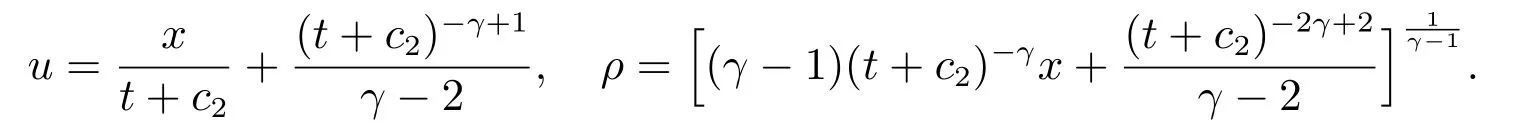
例2在方程组(8)中，取c1(t)=d2(t)=0，可以得到1-维欧拉方程(4)在γ＞1时的解

约束条件(12)和(13)显示c1(t)=d2(t)=0．因此，方程组(9)具有如下形式的解：当γ=1时

当γ＞1时

由此，可以给出n-维欧拉方程(1)如下例中的精确解．

例3取

求解约束条件(13)，我们得到当γ＞1时n-维欧拉方程(1)的精确解

5 结论

总之，由不变子空间方法可以将欧拉方程(1)约化为一阶常微分方程组．基于此，我们可以得到这个方程组的一些精确解．在这里密度为式子d3(t)x2+d2(t)x+d1(t)的函数．当d3(t)＜0时，形如d3(t)x2+d2(t)x+d1(t)的解称为钟形解；当d3(t)＞0时，这种形式的解称为倒钟形解，它们在渗流方程的研究中具有非常重要的作用[9,10]．值得注意的是，渗流方程是由欧拉方程通过Darcy定律给出的．我们希望本文中给出的精确解在欧拉方程的研究中也能发挥一定的作用．另外，由于欧拉方程的非线性性，很难给出其一般解．但是，这里通过不变子空间方法可以得到欧拉方程的一些精确解．我们也希望不变子空间方法能用于更多的非线性偏微分方程(组)的研究中．

参考文献：

[1]Landau L D,Lifshitz E M.Fluid Mechanics(2nd Edition)[M].Oxford:Pergamon Press,1987

[2]Lions P L.Mathematical Topics in Fluid Mechanics 2,Compressible Models[M].Oxford Lecture Series in Mathematics and its Applications,Oxford:Clarendon Press,1998

[3]Liu T P.Compressible flow with damping and vacuum[J].Japan Journal of Industrial and Applied Mathematics,1996,13:25-32

[4]Li T H,Wang D H.Blowup phenomena of solutions to the Euler equations for compressible fluid flow[J].Journal of Differential Equations,2006,221(1):91-101

[5]Yuen M.Perturbational blowup solutions to the compressible 1-dimensional Euler equations[J].Physics Letters A,2011,375(44):3821-3825

[6]Huang S J,Wang R.On blowup phenomena of solutions to the Euler equations for Chaplygin gases[J].Applied Mathematics and Computation,2013,219(9):4365-4370

[7]Galaktionov V A.Invariant subspaces and new explicit solutions to evolution equations with quadratic nonlinearities[J].Proceedings of the Royal Society of Edinburgh,1995,125A(2):225-246

[8]Galaktionov V A,Svirshchevskii S R.Exact Solutions and Invariant Subspaces of Nonlinear Partial Differential Equations in Mechanics and Physics[M].London:Chapman and Hall,2007

[9]Samarskii A A,Galaktionov V A,Kurdyumov S P,et al.Blow-up in Quasilinear Parabolic Equations[M].Berlin,New York:Walter de Gruyter,1995

[10]Galaktionov V A.Geometric Sturmian Theory of Nonlinear Parabolic Equations and Application[M].London:Chapman and Hall,2004

[11]Qu C Z,Zhu C R.Classification of coupled systems with two-component nonlinear diffusion equations by the invariant subspace method[J].Journal of Physics A:Mathematical and Theoretical,2009,42(47):475201

[12]Zhu C R,Qu C Z.Maximal dimension of invariant subspaces admitted by nonlinear vector differential operators[J].Journal of Mathematical Physics,2011,52(4):043507

[13]Zhu C R,Qu C Z.Classification and reduction of generalized thin film equations[J].Communications in Theoretical Physics,2009,52(3):403-410

[14]Shen S F,Qu C Z,Jin Y Y,et al.Maximal dimension of invariant subspaces to systems of nonlinear evolution equations[J].Chinese Annals of Mathematics,2012,33B(2):161-178

[15]Song J Q,Shen S F,Jin Y Y,et al.New maximal dimension of invariant subspaces to coupled systems with two-component equations[J].Communications in Nonlinear Science and Numerical Simulation,2013,18(11):2984-2992

[16]Ma W X,Liu Y P.Invariant subspaces and exact solutions of a class of dispersive evolution equations[J].Communications in Nonlinear Science and Numerical Simulation,2012,17(10):3795-3801